Kompletny przewodnik: jak interpretować wyniki anova w programie excel

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Poniższy przykład zawiera kompletny przewodnik dotyczący interpretacji wyników jednokierunkowej analizy ANOVA w programie Excel.

Przykład: Jak interpretować wyniki ANOVA w Excelu

Załóżmy, że nauczyciel losowo prosi 30 uczniów w swojej klasie, aby przygotowali się do egzaminu jedną z trzech metod nauki.

Poniższy zrzut ekranu przedstawia wyniki uczniów na podstawie zastosowanej metody:

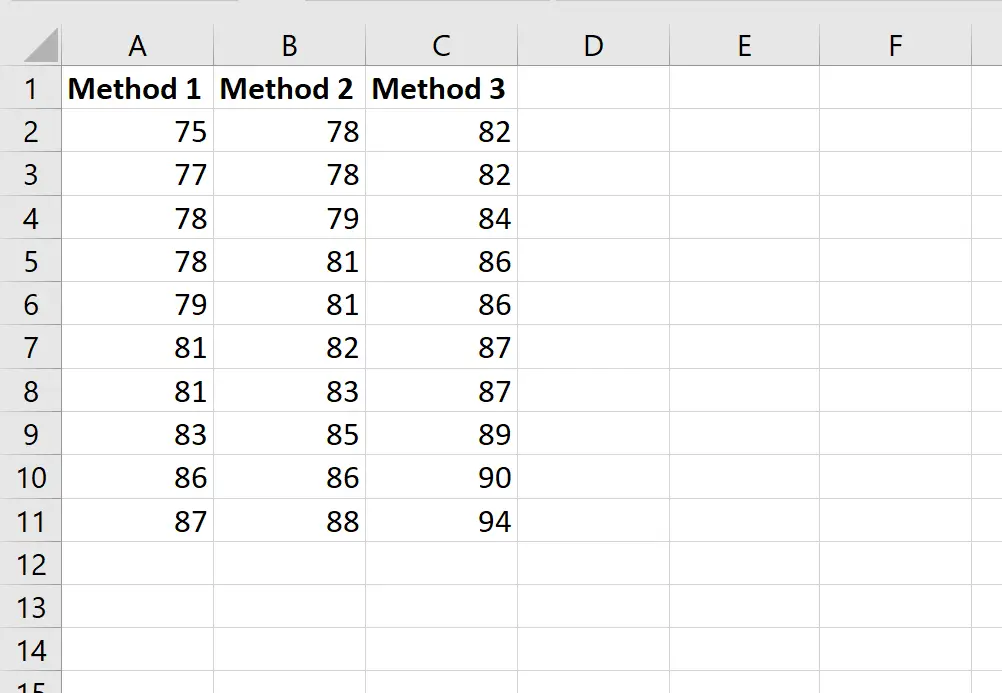
Załóżmy, że nauczyciel chce przeprowadzić jednoczynnikową analizę ANOVA, aby ustalić, czy średnie wyniki są takie same w trzech grupach.

Aby wykonać jednokierunkową analizę ANOVA w programie Excel, kliknij kartę Dane na górnej wstążce, a następnie kliknij opcję Analiza danych w grupie Analizuj .

Jeśli nie widzisz opcji Analiza danych , musisz najpierw załadować darmowe oprogramowanieAnalysis ToolPak .

Po kliknięciu pojawi się nowe okno. Wybierz opcję Anova: Single Factor , a następnie kliknij przycisk OK .

W nowym oknie, które się pojawi, wprowadź następujące informacje:

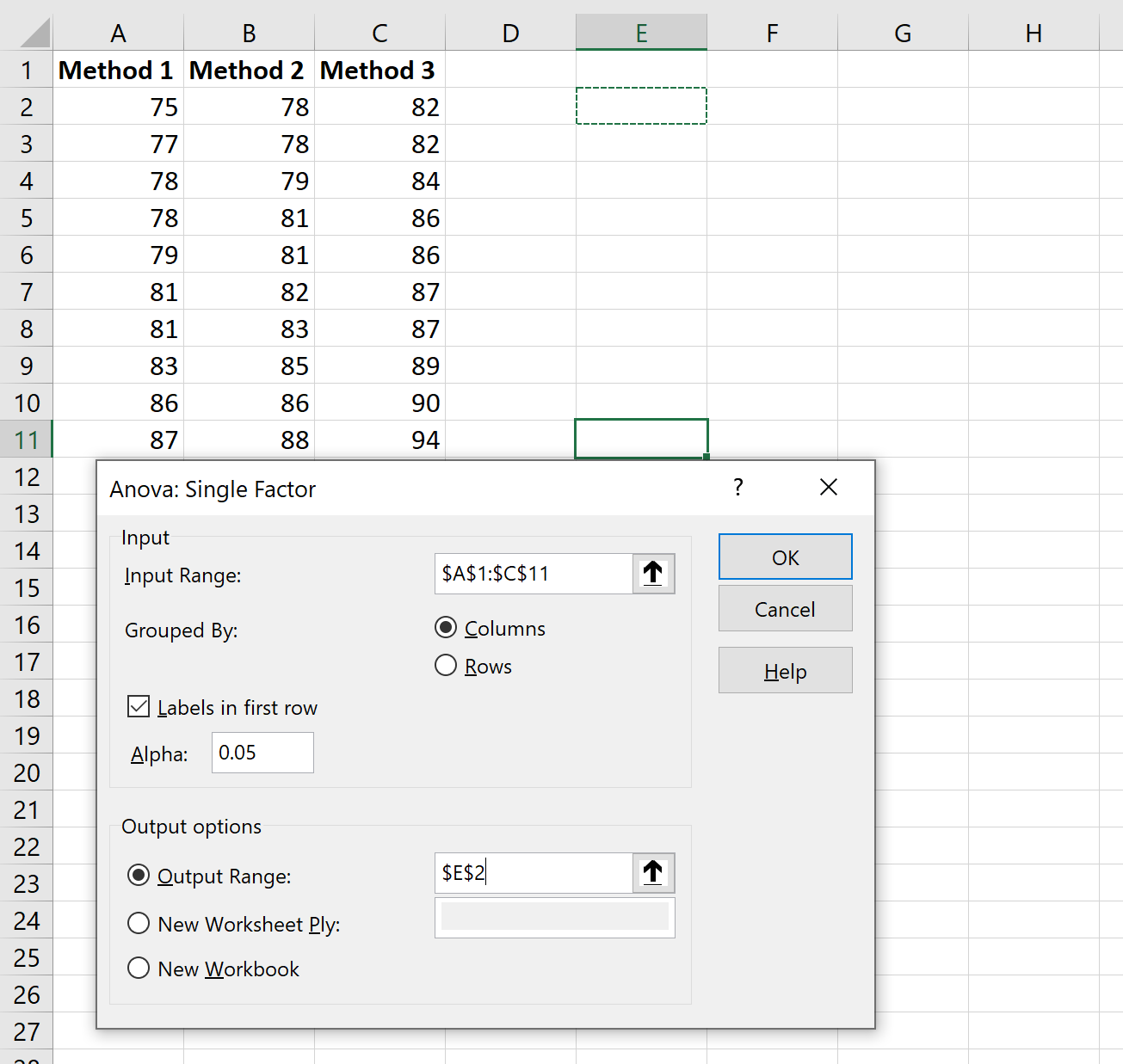
Po kliknięciu OK pojawią się jednokierunkowe wyniki ANOVA:

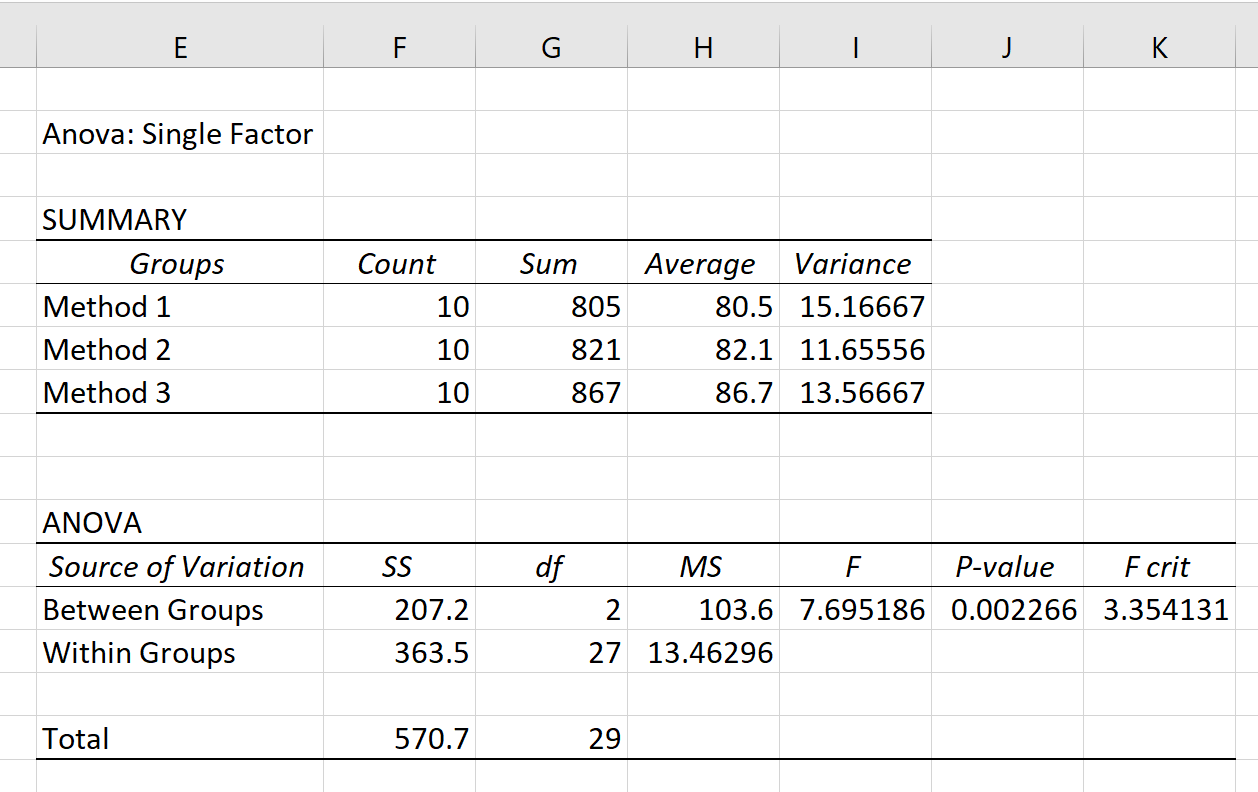
W wyniku zostaną wyświetlone dwie tabele: SUMMARY i ANOVA .

Oto jak interpretować wartości w każdej tabeli:

PODSUMOWANIE tabeli :

• Grupy : Nazwy grup
• Liczba : Liczba obserwacji w każdej grupie
• Suma : Suma wartości każdej grupy
• Średnia : średnia wartość w każdej grupie
• Wariancja : Wariancja wartości w każdej grupie

Ta tabela dostarcza nam kilku przydatnych statystyk podsumowujących dla każdej grupy użytej w ANOVA.

Z tabeli tej wynika, że uczniowie, którzy zastosowali Metodę 3, uzyskali najwyższy średni wynik egzaminu (86,7), ale charakteryzowali się także największą rozbieżnością w wynikach testów. recenzja (13.56667).

Aby określić, czy różnice w średnich grupowych są istotne statystycznie, musimy odwołać się do tabeli ANOVA.

Tabela ANOVA :

• Źródło zmienności : zmierzona zmienność (pomiędzy grupami lub w obrębie grup)
• SS : Suma kwadratów dla każdego źródła zmienności
• df : Stopnie swobody obliczane jako #groups-1 dla df Between i #observations – #groups dla df Within
• MS : Średnia suma kwadratów obliczona w SS/df
• F : Ogólna wartość F, obliczona jako MS pomiędzy / MS w obrębie
• Wartość P : Wartość p odpowiadająca ogólnej wartości F
• Fcrit : Wartość krytyczna F, która odpowiada α = 0,05

Najważniejszą wartością w tej tabeli jest wartość p , która okazuje się wynosić 0,002266 .

Przypomnijmy, że jednokierunkowa analiza ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ : Wszystkie średnie grupowe są równe.
• H _A : Nie wszystkie średnie grupowe są równe.

Ponieważ wartość p jest mniejsza niż α = 0,05, odrzucamy hipotezę zerową jednokierunkowej ANOVA i dochodzimy do wniosku, że mamy wystarczające dowody, aby stwierdzić, że wszystkie średnie grupowe nie są równe.

Oznacza to, że nie wszystkie trzy metody nauki prowadzą do takich samych średnich ocen z egzaminów.

Uwaga : Można także porównać ogólną wartość F z krytyczną wartością F, aby określić, czy należy odrzucić hipotezę zerową. W tym przypadku, ponieważ ogólna wartość F jest większa niż wartość krytyczna F, odrzucilibyśmy hipotezę zerową. Należy zauważyć, że podejście oparte na wartości p i podejście krytycznej wartości F zawsze prowadzą do tego samego wniosku.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać różne analizy ANOVA w programie Excel:

Jak wykonać jednokierunkową ANOVA w programie Excel
Jak wykonać dwukierunkową ANOVA w programie Excel
Jak wykonać powtarzalne pomiary ANOVA w programie Excel
Jak wykonać zagnieżdżoną analizę ANOVA w programie Excel