Co to są zmienne dychotomiczne? (definicja – przykład)

Zmienna dychotomiczna to typ zmiennej, która przyjmuje tylko dwie możliwe wartości.

Oto kilka przykładów zmiennych dychotomicznych:

• Płeć: mężczyzna lub kobieta
• Rzut monetą: orzeł lub reszka
• Typ nieruchomości: mieszkalna lub komercyjna
• Status sportowca: profesjonalista lub amator
• Wyniki egzaminu: zdany lub nie

Tego typu zmienne pojawiają się w praktyce cały czas. Rozważmy na przykład następujący zbiór danych zawierający 10 obserwacji i 4 zmienne:

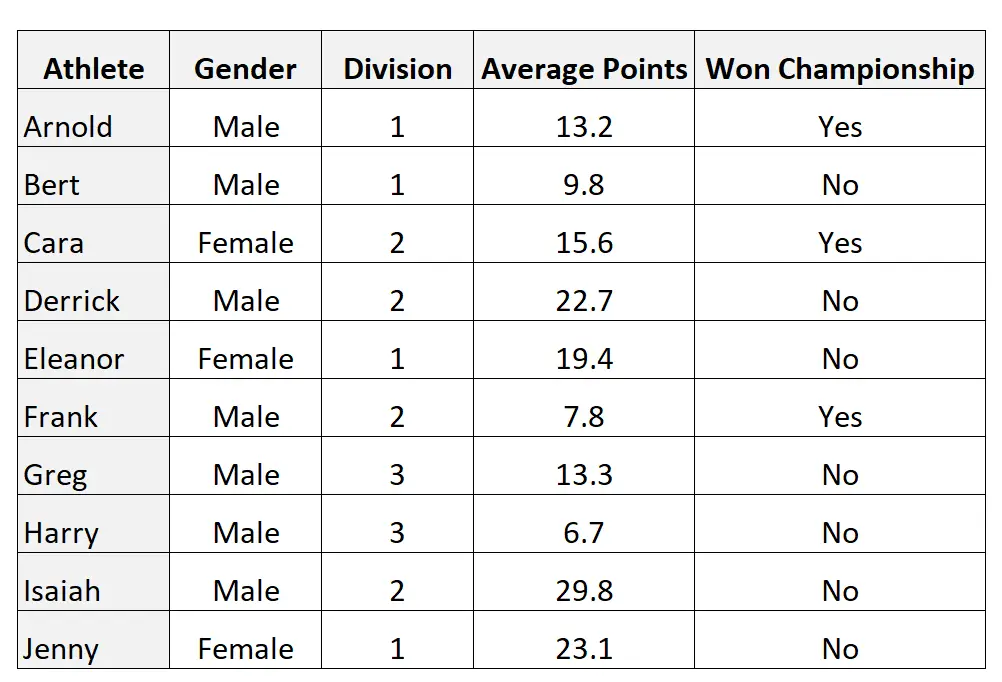
Zmienne płeć i zdobyte mistrzostwa są dychotomiczne, ponieważ każda z nich może przyjmować tylko dwie możliwe wartości:

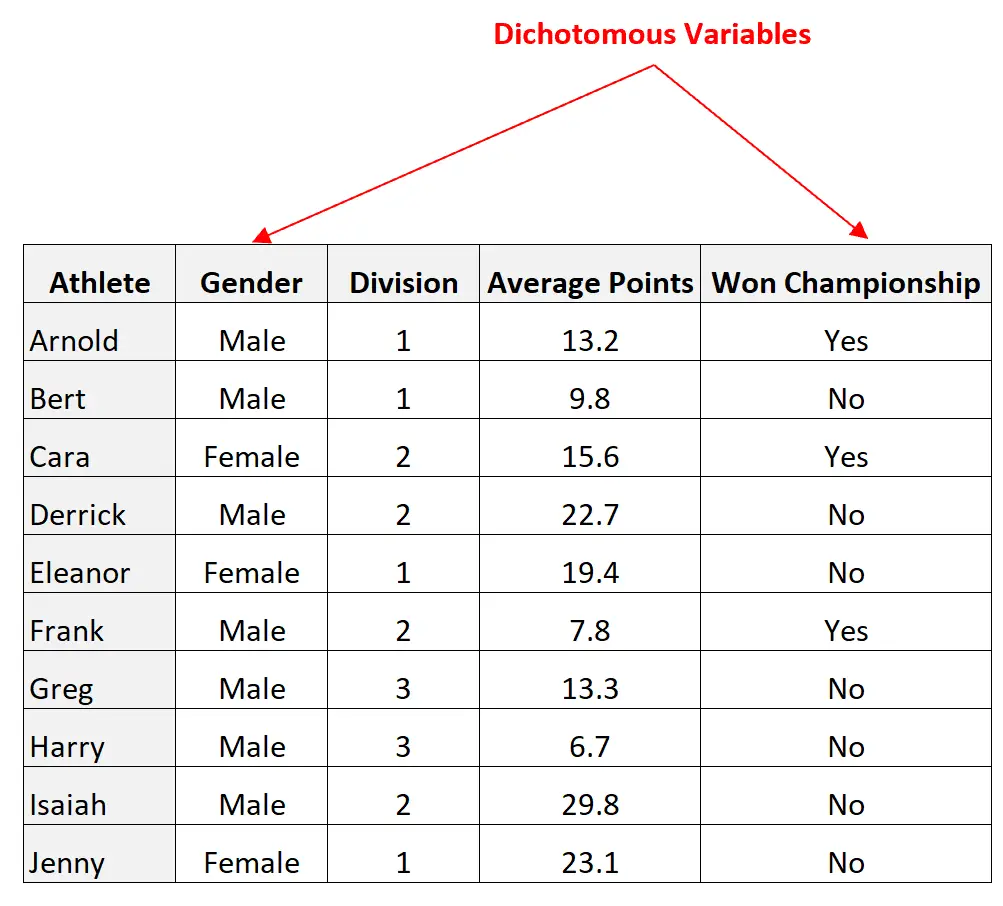
Jednakże zmienne Podział i Średnie punkty nie są dychotomiczne, ponieważ mogą przyjmować wiele wartości.

Dodatkowa wskazówka:

Możesz pamiętać, że zmienne dychotomiczne mogą przyjmować tylko dwie wartości, pamiętając, że przedrostek „di” to greckie słowo oznaczające „dwa”, „dwa razy” lub „podwójne”.

Jak tworzyć zmienne dychotomiczne

Należy zauważyć, że ze zmiennej ciągłej możemy utworzyć zmienną dychotomiczną, po prostu oddzielając wartości w oparciu o określony próg.

Na przykład w poprzednim zbiorze danych mogliśmy przekształcić zmienną Średnia punktów w zmienną dychotomiczną, klasyfikując graczy ze średnią powyżej 15 jako „dobrych strzelców”, a tych ze średnią poniżej 15 jako „złych strzelców”:

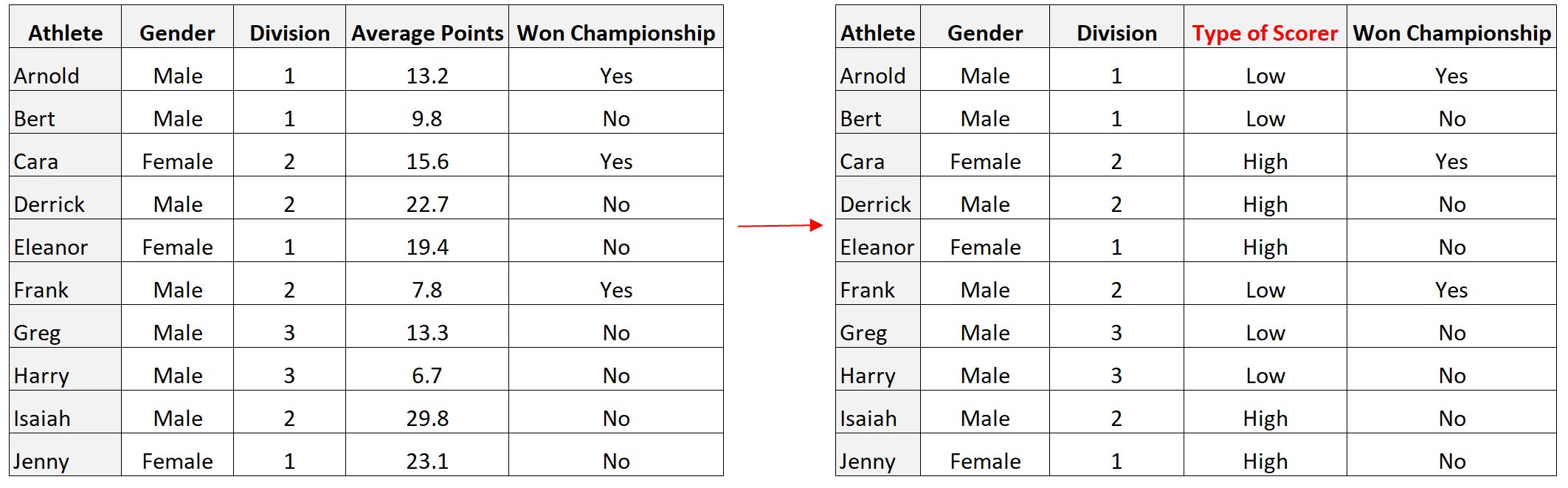
Jak wizualizować zmienne dychotomiczne

Zwykle wizualizujemy zmienne dychotomiczne za pomocą prostego wykresu słupkowego, aby przedstawić częstotliwości każdej wartości, jaką mogą przyjąć.

Na przykład poniższy wykres słupkowy przedstawia częstość występowania każdej płci w poprzednim zbiorze danych:

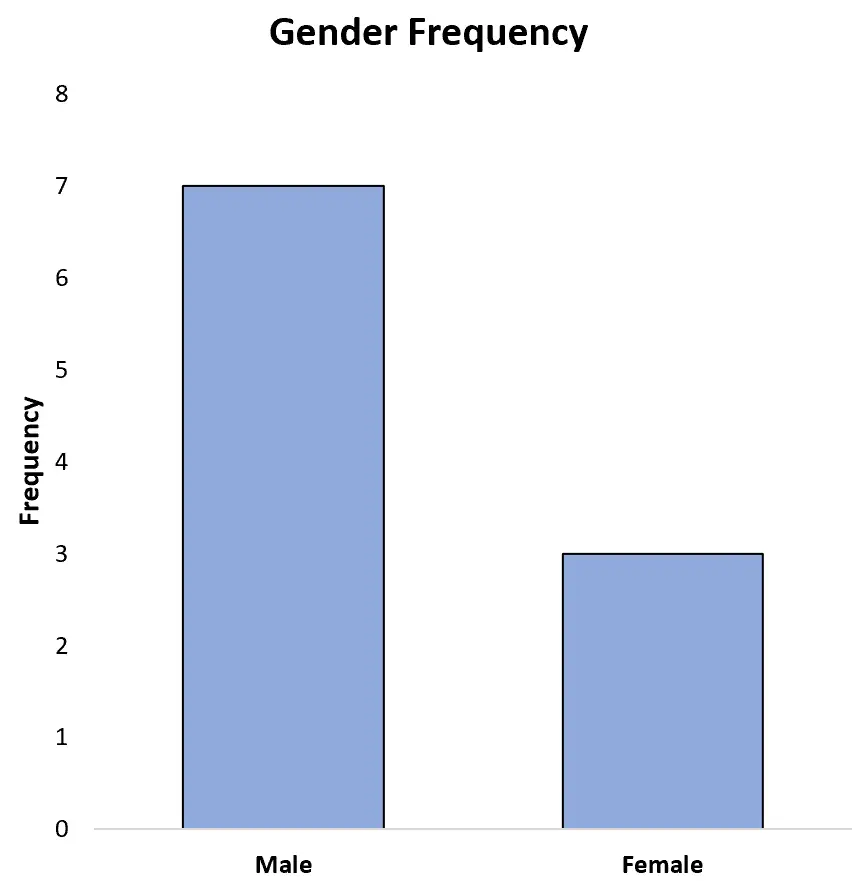
Możemy również wyświetlić częstotliwości jako wartości procentowe na osi Y:

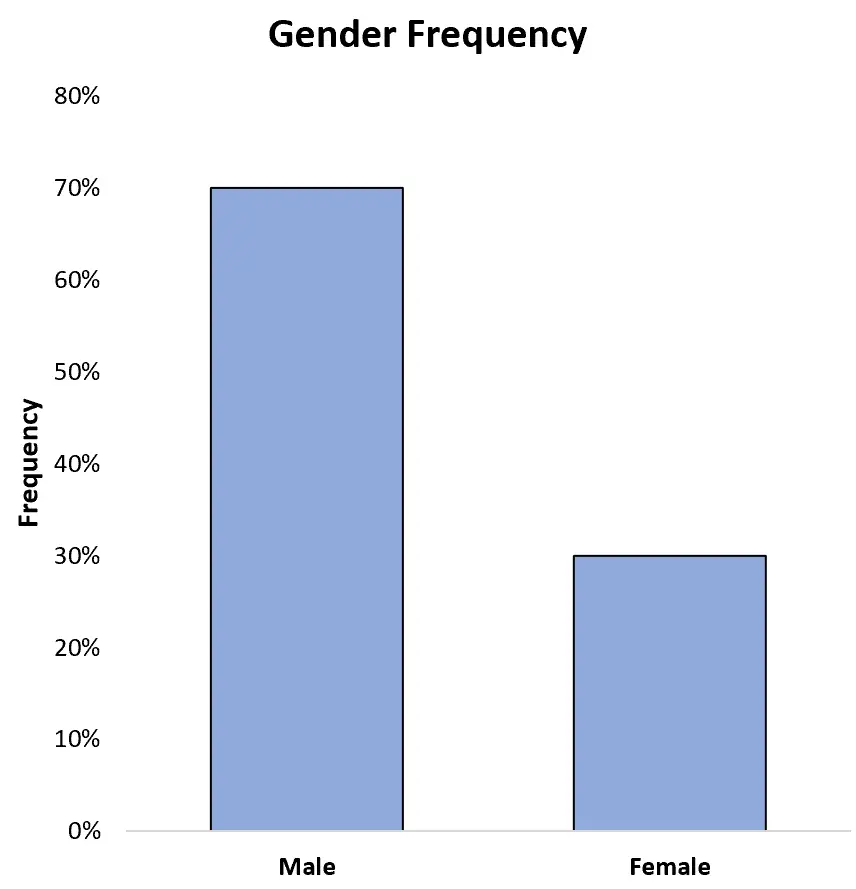
Dzięki temu możemy łatwo zobaczyć, że 70% wszystkich sportowców w zbiorze danych to mężczyźni, a 30% to kobiety.

Jak analizować zmienne dychotomiczne

Istnieje kilka sposobów analizy zmiennych dychotomicznych. Dwie z najpopularniejszych metod to:

1. Test z jednej proporcji

Test z jednej proporcji określa, czy zaobserwowana proporcja jest równa proporcji teoretycznej.

Na przykład moglibyśmy zastosować ten test do ustalenia, czy prawdziwy odsetek sportowców płci męskiej w danej populacji wynosi 50%.

2. Korelacja punktowo-biserialna

Korelacja punktowo-biserialna służy do pomiaru związku między zmienną dychotomiczną a zmienną ciągłą.

Ten typ korelacji przyjmuje wartość od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację między dwiema zmiennymi
• Wartość 0 oznacza brak korelacji między dwiema zmiennymi
• 1 wskazuje na doskonale dodatnią korelację pomiędzy dwiema zmiennymi

Na przykład moglibyśmy obliczyć korelację punktowo-dwseryjną między płcią a średnią liczbą punktów na mecz, aby zrozumieć, jak blisko te dwie zmienne są ze sobą powiązane.