Co to jest myląca zmienna? (definicja – przykład)

W każdym eksperymencie istnieją dwie główne zmienne:

Zmienna niezależna: zmienna, którą eksperymentator modyfikuje lub kontroluje, aby móc obserwować wpływ na zmienną zależną.

Zmienna zależna: zmienna zmierzona w eksperymencie, która jest „zależna” od zmiennej niezależnej.

Badacze są często zainteresowani zrozumieniem, w jaki sposób zmiany zmiennej niezależnej wpływają na zmienną zależną.

Czasami jednak zdarza się, że trzecia zmienna nie jest brana pod uwagę i może mieć to wpływ na związek pomiędzy obiema badanymi zmiennymi.

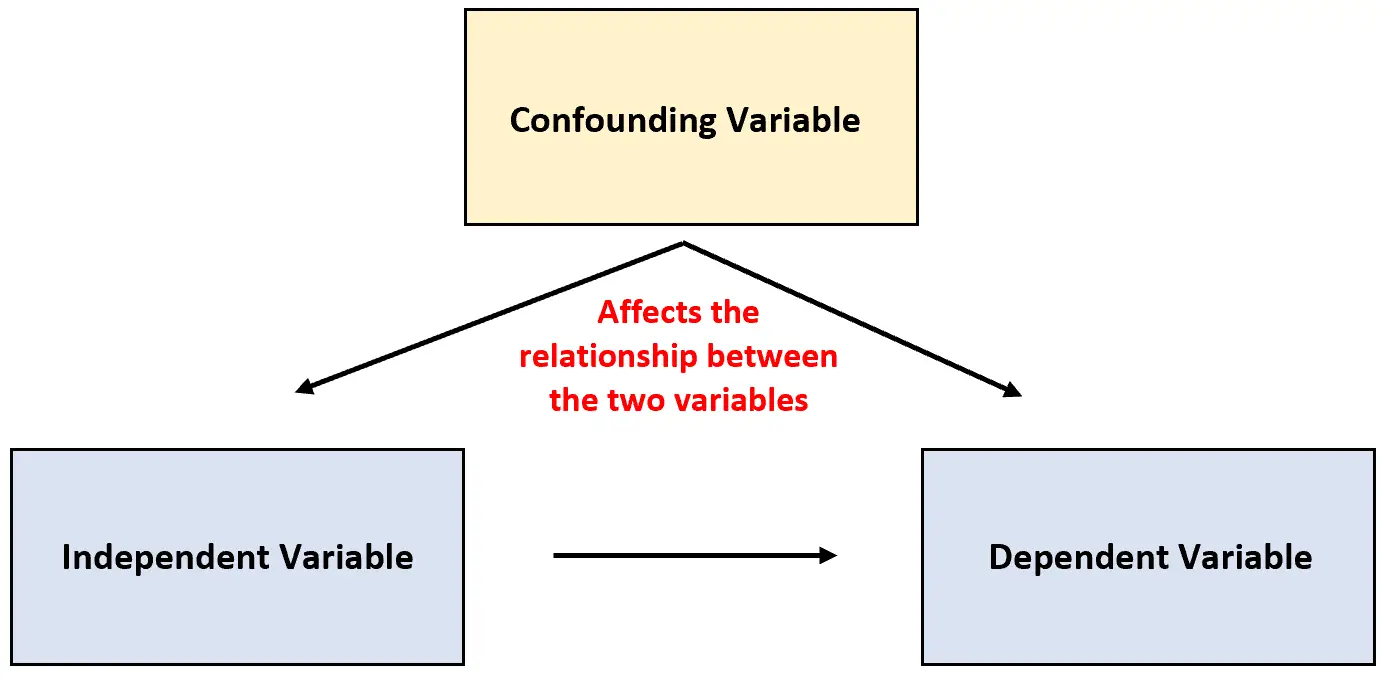
Zmienna tego typu nazywana jest zmienną zakłócającą i może mylić wyniki badania i sprawiać wrażenie, jakby pomiędzy dwiema zmiennymi istniał jakiś związek przyczynowo-skutkowy, który w rzeczywistości nie istnieje.

Zmienna zakłócająca: zmienna, która nie jest uwzględniona w eksperymencie, ale wpływa na związek między dwiema zmiennymi w eksperymencie.

Zmienna tego typu może zakłócić wyniki eksperymentu i prowadzić do niewiarygodnych wyników.

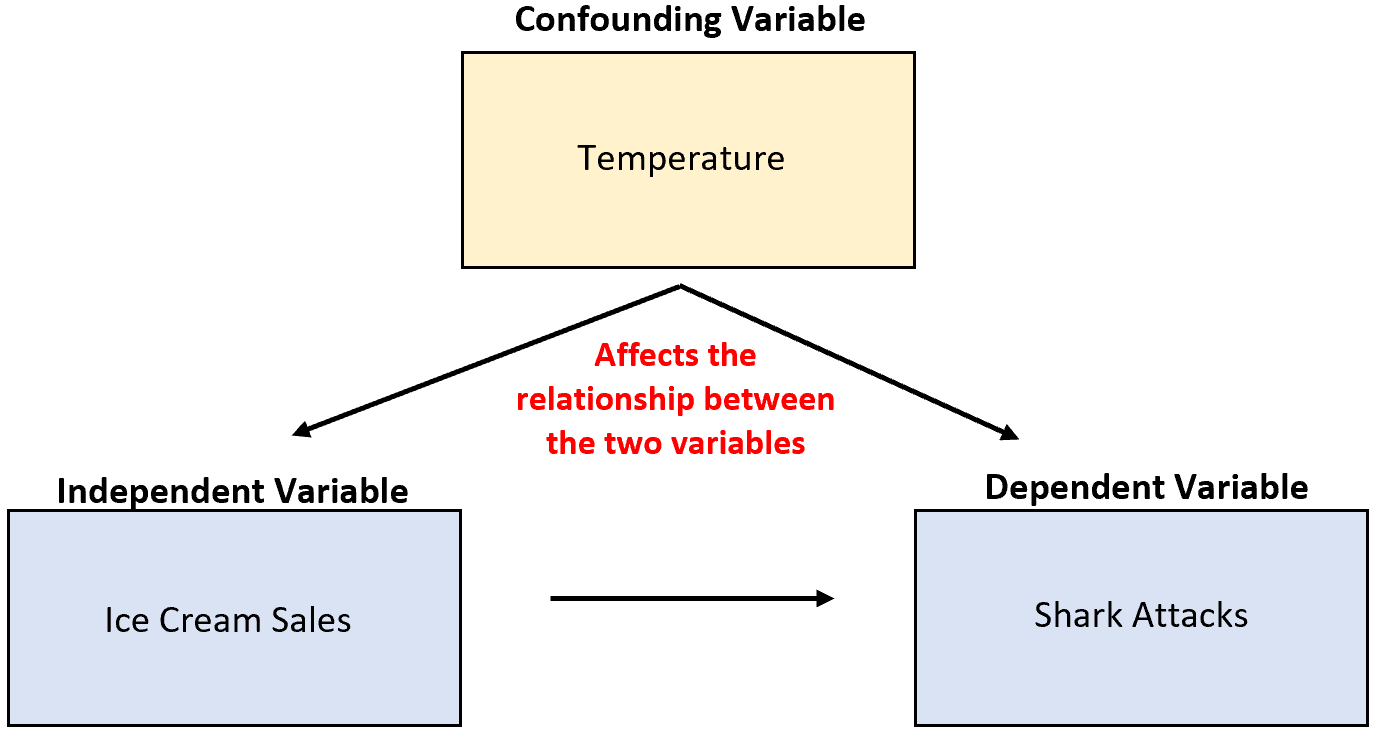
Załóżmy na przykład, że badacz zbiera dane dotyczące sprzedaży lodów i ataków rekinów i odkrywa, że te dwie zmienne są silnie skorelowane. Czy to oznacza, że zwiększona sprzedaż lodów powoduje więcej ataków rekinów?

Jest mało prawdopodobne. Najbardziej prawdopodobną przyczyną jest myląca zmienna temperatura . Kiedy na zewnątrz jest cieplej, więcej osób kupuje lody i więcej osób wybiera się nad ocean.

Wymagania dotyczące zmiennych mylących

Aby zmienna była zmienną mylącą, musi spełniać następujące wymagania:

1. Musi być skorelowana ze zmienną niezależną.

W poprzednim przykładzie temperaturę skorelowano ze zmienną niezależną sprzedaży lodów. W szczególności wyższe temperatury wiążą się z wyższą sprzedażą lodów, a niższe z niższą sprzedażą.

2. Musi istnieć związek przyczynowy ze zmienną zależną.

W poprzednim przykładzie temperatura miała bezpośredni wpływ na liczbę ataków rekinów. W szczególności wyższe temperatury spychają do oceanu więcej ludzi, co bezpośrednio zwiększa prawdopodobieństwo ataków rekinów.

Dlaczego mylenie zmiennych jest problematyczne?

Zmienne zakłócające są problematyczne z dwóch powodów:

1. Zmienne zakłócające mogą sprawiać wrażenie, że istnieją związki przyczynowo-skutkowe, choć tak nie jest.

W naszym poprzednim przykładzie myląca zmienna temperatury sprawiła, że wyglądało na to, że istnieje związek przyczynowy między sprzedażą lodów a atakami rekinów.

Wiemy jednak, że sprzedaż lodów nie powoduje ataków rekinów. Myląca zmienna temperatury sprawia, że tak to wygląda.

2. Zmienne zakłócające mogą przesłaniać prawdziwy związek przyczynowo-skutkowy pomiędzy zmiennymi.

Załóżmy, że badamy zdolność ćwiczeń do obniżenia ciśnienia krwi. Potencjalną zmienną zakłócającą jest masa początkowa, która jest skorelowana z ćwiczeniami i ma bezpośredni wpływ na ciśnienie krwi.

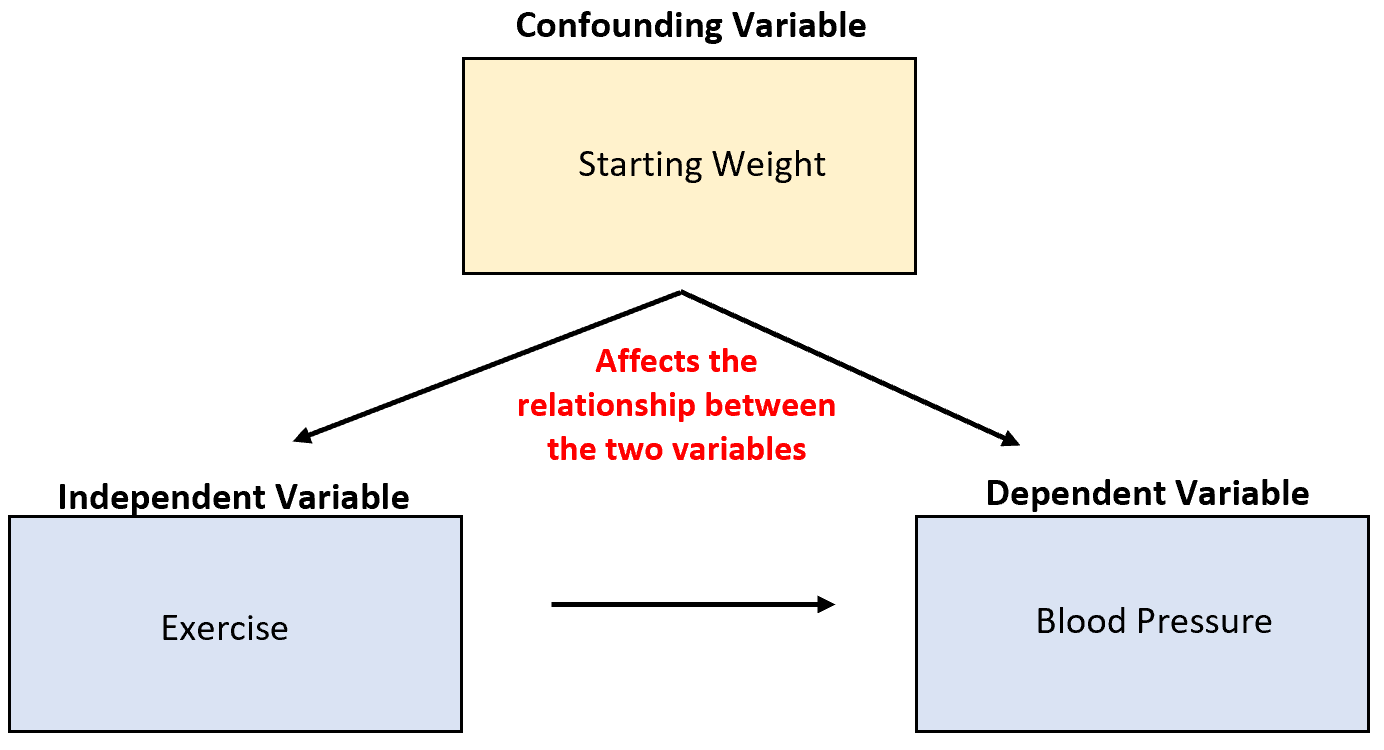
Chociaż wzmożona aktywność fizyczna może prowadzić do obniżenia ciśnienia krwi, duży wpływ na związek między tymi dwiema zmiennymi ma również wyjściowa masa ciała danej osoby.

Zmienne zakłócające i ważność wewnętrzna

Z technicznego punktu widzenia zmienne zakłócające wpływają na wewnętrzną trafność badania, która odnosi się do zasadności przypisywania wszelkich zmian zmiennej zależnej zmianom zmiennej niezależnej.

Gdy występują zmienne zakłócające, nie zawsze możemy z całą pewnością stwierdzić, że zmiany, które obserwujemy w zmiennej zależnej, są bezpośrednim skutkiem zmian w zmiennej niezależnej.

Jak zmniejszyć efekt mylących zmiennych

Istnieje kilka sposobów ograniczenia efektu mylących zmiennych, w tym następujące metody:

1. Losowy przydział

Losowe przypisanie odnosi się do procesu losowego przydzielania osób biorących udział w badaniu do grupy terapeutycznej lub grupy kontrolnej.

Załóżmy na przykład, że chcemy zbadać wpływ nowej pigułki na ciśnienie krwi. Jeśli do badania zrekrutujemy 100 osób, możemy użyć generatora liczb losowych, aby losowo przydzielić 50 osób do grupy kontrolnej (bez pigułki) i 50 osób do grupy leczonej (nowa pigułka).

Stosując losowe przypisanie, zwiększamy szansę, że obie grupy będą miały mniej więcej podobne cechy, co oznacza, że wszelkie różnice zaobserwowane między obiema grupami można przypisać leczeniu.

Oznacza to, że badanie musi mieć wiarygodność wewnętrzną : wszelkie różnice w ciśnieniu krwi pomiędzy grupami można przypisać samej pigułce, w przeciwieństwie do różnic pomiędzy osobami w grupach.

2. Blokowanie

Blokowanie odnosi się do praktyki dzielenia osób biorących udział w badaniu na „bloki” w oparciu o pewną wartość zmiennej zakłócającej w celu wyeliminowania wpływu zmiennej zakłócającej.

Załóżmy na przykład, że badacze chcą zrozumieć wpływ nowej diety na utratę wagi. Zmienną niezależną jest nowa dieta, a zmienną zależną jest stopień utraty wagi.

Jednak jedną zmienną zakłócającą, która może powodować różnice w utracie wagi, jest płeć . Jest prawdopodobne, że płeć danej osoby będzie miała wpływ na ilość utraconej wagi, niezależnie od tego, czy nowa dieta będzie skuteczna, czy nie.

Jednym ze sposobów rozwiązania tego problemu jest umieszczenie osób w jednym z dwóch bloków:

• Mężczyzna
• Kobieta

Następnie w ramach każdego bloku losowo przydzielaliśmy poszczególne osoby do jednego z dwóch sposobów leczenia:

• Nowa dieta
• Standardowa dieta

Dzięki temu różnice w obrębie każdego bloku byłyby znacznie mniejsze niż różnice między wszystkimi osobami i moglibyśmy lepiej zrozumieć, w jaki sposób nowa dieta wpływa na utratę wagi, kontrolując seks.

3. Korespondencja

Projekt dopasowanych par to rodzaj projektu eksperymentalnego, w którym „dopasowujemy” osoby na podstawie wartości potencjalnych zmiennych zakłócających.

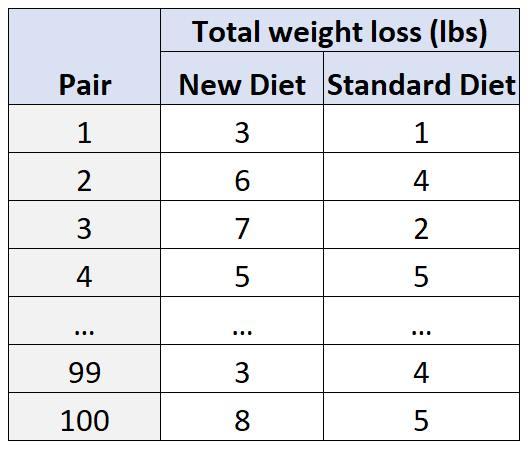
Załóżmy na przykład, że badacze chcą wiedzieć, jak nowa dieta wpływa na utratę wagi w porównaniu ze standardową dietą. Dwie potencjalne mylące zmienne w tej sytuacji to wiek i płeć .

Aby to uwzględnić, zrekrutuj badaczy 100 osób, a następnie podziel ich na 50 par w zależności od wieku i płci. Na przykład:

• 25-letni mężczyzna zostanie dobrany do innego 25-letniego mężczyzny, ponieważ „pasują” pod względem wieku i płci.
• 30-letnia kobieta zostanie dobrana do innej 30-letniej kobiety, ponieważ pasują one również pod względem wieku, płci itp.

Następnie w każdej parze jeden pacjent zostanie losowo przydzielony do stosowania nowej diety przez 30 dni, a drugi do stosowania standardowej diety przez 30 dni.

Pod koniec 30 dni badacze zmierzą całkowitą utratę masy ciała u każdego pacjenta.

Stosując tego typu projekt, badacze mogą być pewni, że wszelkie różnice w utracie wagi można przypisać rodzajowi stosowanej diety, a nie zakłócającym zmiennym, takim jak wiek i płeć .

Ten typ konstrukcji ma kilka wad, do których należą:

1. Stracić dwóch poddanych, jeśli jeden z nich odpadnie. Jeśli pacjent zdecyduje się zrezygnować z badania, w rzeczywistości tracisz dwóch uczestników, ponieważ nie masz już pełnej pary.

2. Znalezienie dopasowań wymaga czasu . Znalezienie tematów pasujących do określonych zmiennych, takich jak płeć i wiek, może być czasochłonne.

3. Nie można idealnie dopasować tematów . Bez względu na to, jak bardzo się starasz, zawsze będą różnice w tematach każdej pary.

Jeśli jednak w badaniu dostępne są zasoby umożliwiające wdrożenie tego projektu, może ono być bardzo skuteczne w eliminowaniu skutków zmiennych zakłócających.