Niezależna zmienna

W tym artykule wyjaśniono, czym są zmienne niezależne. W ten sposób znajdziesz znaczenie zmiennej niezależnej w matematyce i statystyce, a także zobaczysz kilka przykładów tego typu zmiennej.

Co to jest zmienna niezależna?

Zmienna niezależna to zmienna, której wartość nie zależy od wartości żadnej innej zmiennej. I odwrotnie, jeśli zmienna niezależna zmienia swoją wartość, zmienia to wartość zmiennej zależnej.

Kiedy przedstawiasz wykres zmiennej niezależnej, jest ona zwykle reprezentowana przez literę x i na osi x (oś pozioma).

Na przykład długość wynajmu nieruchomości jest zmienną niezależną wpływającą na cenę, jaką płacisz. Ponieważ czas trwania wynajmu można określić, a jego wartość wpływa na zmienną zależną od ceny, ponieważ im dłużej obiekty są używane, tym więcej muszą zapłacić.

Zmienne niezależne można również nazwać zmiennymi objaśniającymi, zmiennymi wejściowymi lub zmiennymi manipulowanymi.

Przykłady zmiennych niezależnych

Po zapoznaniu się z definicją zmiennej niezależnej, spójrzmy teraz na kilka przykładów tego typu zmiennej, aby lepiej zrozumieć tę koncepcję.

• Czas spędzony na nauce (zmienna niezależna) wpływa na uzyskiwane oceny (zmienna zależna).
• Cena produktu (zmienna niezależna) zmienia liczbę osób chcących kupić produkt (zmienna zależna).
• Temperatura otoczenia (zmienna niezależna) wpływa na liczbę pożarów lasów (zmienna zależna).
• Reklama prowadzona dla produktu (zmienna niezależna) ma wpływ na wielkość sprzedaży tego produktu (zmienna zależna).
• Liczba mieszkańców miasta (zmienna niezależna) jest powiązana z liczbą taksówek w mieście (zmienna zależna).

Zmienna niezależna w matematyce

W matematyce związek przyczynowo-skutkowy jest zwykle modelowany przy użyciu zmiennej niezależnej i zmiennej zależnej. Zatem funkcja definiuje matematyczną zależność istniejącą pomiędzy zmienną niezależną a zmienną zależną.

Zmienne niezależne są zwykle oznaczane literą x , natomiast litera y jest używana w przypadku zmiennych zależnych.

Na przykład funkcja y=2x wskazuje, że gdy zmienna niezależna x wzrośnie o jedną jednostkę, zmienna zależna y wzrośnie dwukrotnie bardziej.

Aby dowiedzieć się więcej o funkcjach matematycznych, zalecamy odwiedzenie strony internetowej naszego partnerafunction.xyz .

Zmienne niezależne w statystyce

Jednak w rzeczywistości bardzo trudno jest znaleźć związek między dwiema zmiennymi, który można określić za pomocą dokładnej funkcji matematycznej, ponieważ czasami ta sama wartość zmiennej niezależnej skutkuje inną wartością zmiennej zależnej.

Na przykład czasami, ucząc się więcej, otrzymujemy niższą ocenę lub odwrotnie, ucząc się mniej, uzyskujemy lepszą ocenę. Dlatego liczba godzin, które spędzamy na nauce, nie jest jedynym czynnikiem wpływającym na uzyskaną ocenę, może się ona różnić w zależności od trudności egzaminu lub trudności studiowanego przedmiotu.

Dlatego w statystyce zwykle przeprowadza się wiele eksperymentów w celu ustalenia, czy istnieje związek między zmienną niezależną a zmienną zależną. Uzyskane wyniki można następnie przedstawić graficznie, aby sprawdzić, czy zmienne są powiązane, a jeśli tak, jaki rodzaj relacji między nimi (dodatni, ujemny, liniowy, wykładniczy itp.).

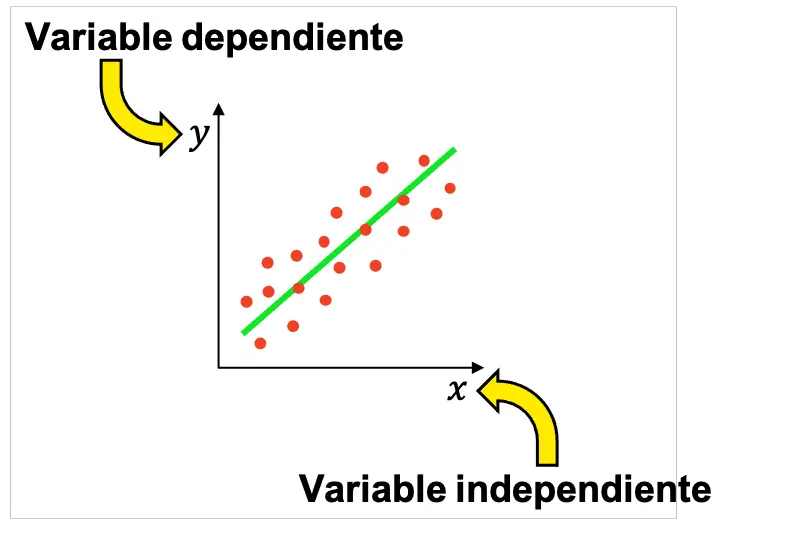
Należy pamiętać, że w badaniu może występować więcej niż jedna zmienna niezależna, chociaż najbardziej podstawowe badania statystyczne przeprowadza się z jedną zmienną niezależną i jedną zależną.

Po przeprowadzeniu badania statystycznego można obliczyć funkcję matematyczną, która pozwala na dokonanie przybliżenia i tym samym zamodelowanie zależności pomiędzy zmiennymi. Zwykle najpierw tworzy się model statystyczny, a następnie model matematyczny.