Zmienna zależna i niezależna

W tym artykule wyjaśniono, czym są zmienne zależne i niezależne. W ten sposób dowiesz się, jaka jest różnica między zmienną zależną a zmienną niezależną, jak poznać, która zmienna jest zależna, a która niezależna, a ponadto przedstawiono kilka przykładów tego typu zmiennej.

Co to jest zmienna zależna i niezależna?

Zmienna zależna to zmienna, której wartość zależy od innej zmiennej, będącej zmienną niezależną . Dlatego różnica między zmienną zależną a zmienną niezależną polega na tym, że zmienna niezależna nie zależy od żadnej innej zmiennej, ale zmienna zależna zależy od wartości zmiennej niezależnej.

Na wykresie zmienna niezależna jest reprezentowana przez literę x na odciętej (oś pozioma), natomiast zmienna zależna jest reprezentowana przez literę y na rzędnej (oś pionowa).

Przykładowo, jeśli w badaniu statystycznym przeanalizujemy związek pomiędzy uzyskaną oceną a godzinami poświęconymi na naukę, to poświęcone na naukę godziny są zmienną niezależną, a uzyskana ocena zmienną zależną. Bo uzyskana ocena zależy od przepracowanych godzin, a nie odwrotnie.

Przykłady zmiennych zależnych i niezależnych

W poprzedniej sekcji widzieliśmy definicję zmiennych zależnych i niezależnych, więc teraz zobaczymy dziesięć przykładów tego typu zmiennej, aby lepiej zrozumieć jej znaczenie.

1. Czas spędzony na nauce (zmienna niezależna) wpływa na uzyskiwane oceny (zmienna zależna).
2. Cena produktu (zmienna niezależna) zmienia liczbę osób chcących kupić produkt (zmienna zależna).
3. Zdrowie człowieka (zmienna zależna) zależy od diety (zmienna niezależna).
4. Na tętno danej osoby (zmienna zależna) wpływa jej wysokość (zmienna niezależna).
5. Temperatura otoczenia (zmienna niezależna) wpływa na liczbę pożarów lasów (zmienna zależna).
6. Poziom satysfakcji klienta (zmienna zależna) ewoluuje w zależności od jakości świadczonej usługi (zmienna niezależna).
7. Reklama produktu (zmienna niezależna) ma wpływ na wielkość sprzedaży tego produktu (zmienna zależna).
8. Ilość substancji zanieczyszczających emitowanych przez kraj (zmienna zależna) zależy od produkcji przemysłowej tego kraju (zmienna niezależna).
9. Wynagrodzenie taksówkarza (zmienna zależna) jest zróżnicowane w zależności od liczby odbywanych przez niego kursów (zmienna niezależna).
10. Liczba mieszkańców miasta (zmienna niezależna) jest powiązana z liczbą taksówek w mieście (zmienna zależna).

Należy pamiętać, że zmienna jest zależna lub niezależna w zależności od kontekstu, ponieważ w zależności od badania będzie działać jako przyczyna lub skutek związku.

Ćwiczenia ze zmiennymi zależnymi i niezależnymi

Która zmienna zależna, a która niezależna, jest w poniższych przypadkach?

1. Liczba mieszkańców miasta – Liczba autobusów komunikacji miejskiej
2. Wiek pojazdu – Stan pojazdu
3. Liczba komarów – Temperatura otoczenia
4. Liczba dni deszczowych w miesiącu – Zapotrzebowanie na parasole

1. Zmienna zależna: Liczba autobusów komunikacji miejskiej – Zmienna niezależna: Liczba mieszkańców miasta
2. Zmienna zależna: Stan pojazdu – Zmienna niezależna: Wiek pojazdu
3. Zmienna zależna: Liczba komarów – Zmienna niezależna: Temperatura otoczenia
4. Zmienna zależna: Zapotrzebowanie na parasole – Zmienna niezależna: Liczba dni deszczowych w miesiącu

Zmienna zależna i niezależna w matematyce

W matematyce związek przyczynowo-skutkowy jest zwykle modelowany przy użyciu zmiennej niezależnej i zmiennej zależnej. Zatem funkcja definiuje matematyczną zależność istniejącą pomiędzy zmienną zależną a zmienną niezależną.

Zmienne zależne są zwykle oznaczane literą y , natomiast litera x jest powszechnie używana do wskazania zmiennych niezależnych.

Na przykład funkcja y=2x wskazuje, że gdy zmienna niezależna x wzrośnie o jedną jednostkę, zmienna zależna y wzrośnie dwukrotnie bardziej.

Aby dowiedzieć się więcej o funkcjach matematycznych, odwiedź witrynę naszego partnera, function.xyz .

Zmienna zależna i niezależna w statystyce

Jednak w rzeczywistości bardzo trudno jest znaleźć związek między dwiema zmiennymi, który można określić za pomocą dokładnej funkcji matematycznej, ponieważ czasami ta sama wartość zmiennej niezależnej skutkuje inną wartością zmiennej zależnej.

Na przykład czasami, ucząc się więcej, otrzymujemy niższą ocenę lub odwrotnie, ucząc się mniej, uzyskujemy lepszą ocenę. Dlatego liczba godzin, które poświęcamy na naukę, nie jest jedynym czynnikiem wpływającym na uzyskaną ocenę, może się ona różnić w zależności od trudności egzaminu lub trudności studiowanego materiału.

Z tego powodu w statystyce zwykle przeprowadza się wiele eksperymentów, aby ustalić, czy istnieje związek między dwiema zmiennymi, z których jedna będzie zmienną niezależną, a druga zmienną zależną. Następnie uzyskane wyniki można przedstawić graficznie, aby sprawdzić, czy zmienne są powiązane, a jeśli tak, jaki rodzaj relacji między nimi (dodatni, ujemny, liniowy, wykładniczy itp.).

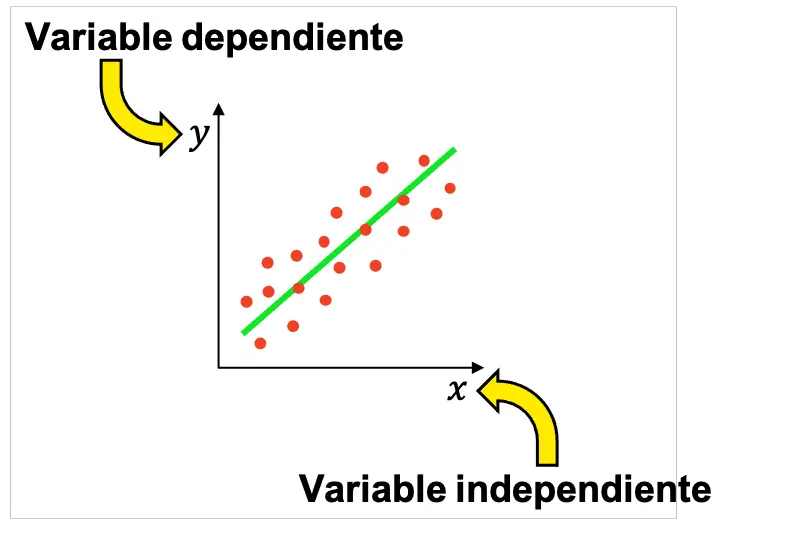
Należy pamiętać, że w badaniu może występować więcej niż jedna zmienna niezależna, chociaż najbardziej podstawowe badania statystyczne przeprowadza się z jedną zmienną niezależną i jedną zależną.

Po przeprowadzeniu badania statystycznego można obliczyć funkcję matematyczną w celu uzyskania przybliżenia i modelowania zależności między zmiennymi. Zwykle najpierw tworzony jest model statystyczny, a następnie model matematyczny.