Jak używać zmiennych fikcyjnych w analizie regresji

Regresja liniowa to metoda, którą możemy zastosować do ilościowego określenia związku między jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Zwykle używamy regresji liniowej ze zmiennymi ilościowymi . Czasami nazywane zmiennymi „numerycznymi” i są to zmienne reprezentujące mierzalną wielkość. Przykłady obejmują:

• Liczba metrów kwadratowych w domu
• Wielkość populacji miasta
• Wiek osobnika

Czasami jednak chcemy użyć zmiennych kategorycznych jako zmiennych predykcyjnych. Są to zmienne, które przyjmują nazwy lub etykiety i można je podzielić na kategorie. Przykłady obejmują:

• Kolor oczu (np. „niebieski”, „zielony”, „brązowy”)
• Płeć (np. „mężczyzna”, „kobieta”)
• Stan cywilny (np. „żonaty”, „panny”, „rozwiedziony”)

Używając zmiennych kategorycznych, nie ma sensu po prostu przypisywać wartości takich jak 1, 2, 3 do wartości takich jak „niebieski”, „zielony” i „brązowy”, ponieważ nie ma sensu mówić ten zielony jest podwójny. tak kolorowy jak niebieski lub brązowy jest trzy razy bardziej kolorowy niż niebieski.

Zamiast tego rozwiązaniem jest użycie zmiennych fikcyjnych . Są to zmienne, które tworzymy specjalnie na potrzeby analizy regresji i które przyjmują jedną z dwóch wartości: zero lub jeden.

Zmienne fikcyjne: Zmienne numeryczne używane w analizie regresji do reprezentowania danych kategorycznych, które mogą przyjmować tylko jedną z dwóch wartości: zero lub jeden.

Liczba zmiennych fikcyjnych, które musimy utworzyć, jest równa k -1, gdzie k jest liczbą różnych wartości, jakie może przyjąć zmienna kategoryczna.

Poniższe przykłady ilustrują sposób tworzenia zmiennych fikcyjnych dla różnych zestawów danych.

Przykład 1: Utwórz zmienną fikcyjną zawierającą tylko dwie wartości

Załóżmy, że mamy następujący zestaw danych i chcemy wykorzystać płeć i wiek do przewidywania dochodów :

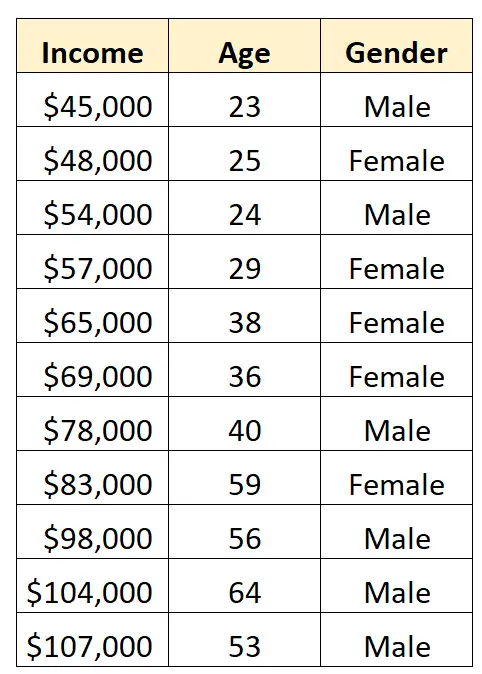
Aby użyć płci jako zmiennej predykcyjnej w modelu regresji, musimy przekształcić ją w zmienną fikcyjną.

Ponieważ jest to obecnie zmienna kategoryczna, która może przyjmować dwie różne wartości („Mężczyzna” lub „Kobieta”), po prostu tworzymy zmienną fikcyjną k -1 = 2-1 = 1.

Aby utworzyć tę fikcyjną zmienną, możemy wybrać jedną z wartości („Mężczyzna” lub „Kobieta”), która będzie reprezentować 0, a druga będzie reprezentować 1.

Ogólnie rzecz biorąc, najczęściej reprezentujemy najczęstszą wartość za pomocą 0, co w tym zbiorze danych oznaczałoby „Mężczyzna”.

Oto jak przekonwertować płeć na zmienną fikcyjną:

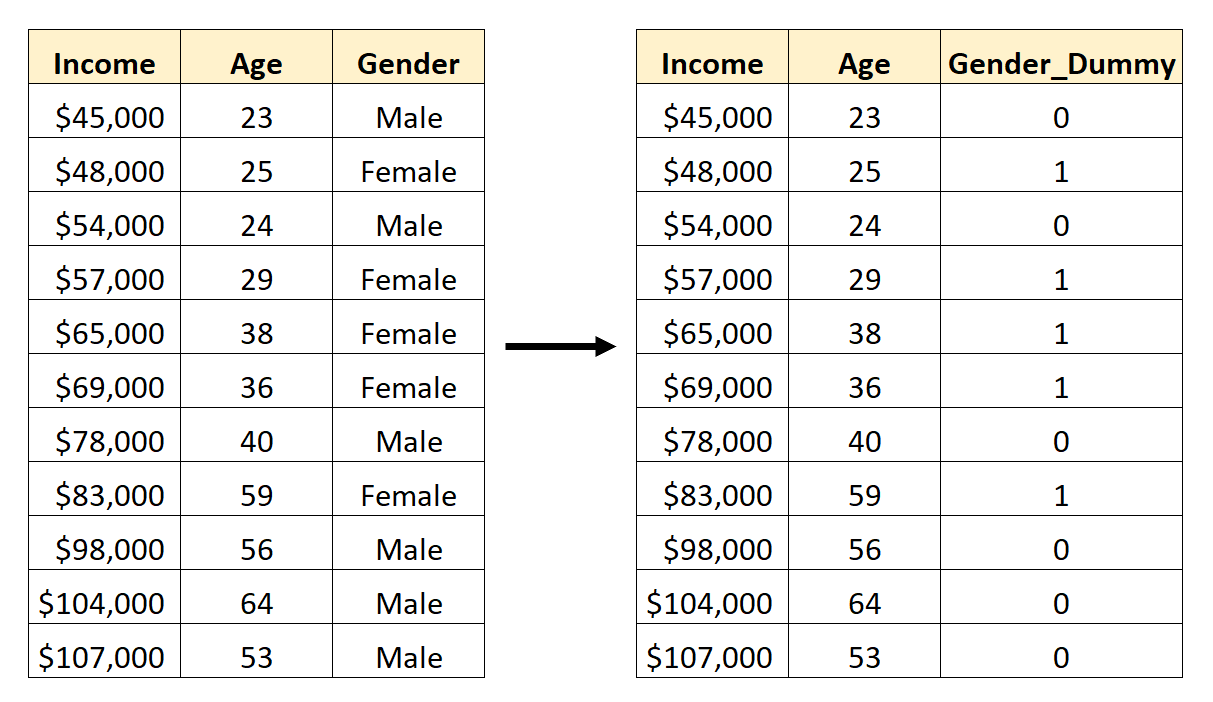
Moglibyśmy następnie użyć Age i Gender_Dummy jako zmiennych predykcyjnych w modelu regresji.

Przykład 2: Utwórz zmienną fikcyjną z wieloma wartościami

Załóżmy, że mamy następujący zestaw danych i chcemy wykorzystać stan cywilny i wiek do przewidywania dochodów :

Aby wykorzystać stan cywilny jako zmienną predykcyjną w modelu regresji, musimy przekształcić go w zmienną fikcyjną.

Ponieważ jest to obecnie zmienna kategoryczna, która może przyjmować trzy różne wartości („Singiel”, „Żonaty” lub „Rozwiedziony”), musimy utworzyć k -1 = 3-1 = 2 zmienne fikcyjne.

Aby utworzyć tę fikcyjną zmienną, możemy pozostawić „Single” jako wartość bazową, ponieważ pojawia się ona najczęściej. Oto jak przekształcilibyśmy stan cywilny w zmienne fikcyjne:

Moglibyśmy następnie użyć Wiek , Żonaty i Rozwiedziony jako zmiennych predykcyjnych w modelu regresji.

Jak interpretować wyniki regresji ze zmiennymi fikcyjnymi

Załóżmy, że dopasowujemy model regresji liniowej wielokrotnej , korzystając ze zbioru danych z poprzedniego przykładu, w którym Wiek , Żonaty i Rozwiedziony jako zmienne predykcyjne oraz Dochód jako zmienna odpowiedzi.

Oto wynik regresji:

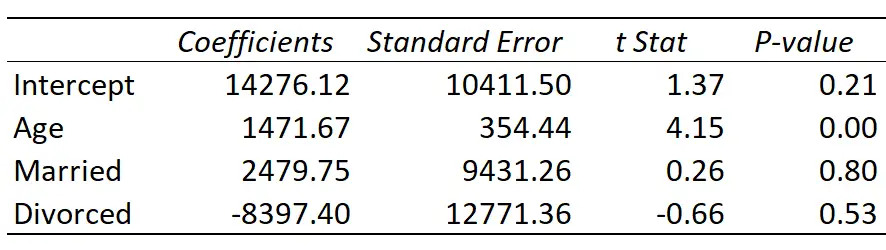
Dopasowaną linię regresji definiuje się jako:

Dochód = 14 276,21 + 1 471,67* (wiek) + 2 479,75* (mężatka) – 8 397,40* (rozwiedziony)

Możemy użyć tego równania, aby znaleźć szacunkowy dochód danej osoby na podstawie jej wieku i stanu cywilnego. Na przykład osoba w wieku 35 lat i będąca w związku małżeńskim miałaby szacunkowy dochód w wysokości 68 264 dolarów :

Dochód = 14 276,21 + 1 471,67*(35) + 2 479,75*(1) – 8 397,40*(0) = 68 264 USD

Oto jak interpretować współczynniki regresji w tabeli:

• Przecięcie: Przecięcie oznacza średni dochód samotnej osoby w wieku zero. Oczywiście nie można mieć lat zerowych, więc nie ma sensu interpretować samego wyrazu wolnego w tym konkretnym modelu regresji.
• Wiek: każdy rok podwyższenia wieku wiąże się ze średnim wzrostem dochodu o 1471,67 USD. Ponieważ wartość p (0,00) jest mniejsza niż 0,05, wiek jest statystycznie istotnym predyktorem dochodów.
• Żonaty: osoba zamężna zarabia średnio o 2479,75 dolarów więcej niż osoba samotna. Ponieważ wartość p (0,80) jest nie mniejsza niż 0,05, różnica ta nie jest istotna statystycznie.
• Rozwiedziony: osoba rozwiedziona zarabia średnio 8 397,40 dolarów mniej niż osoba samotna. Ponieważ wartość p (0,53) jest nie mniejsza niż 0,05, różnica ta nie jest istotna statystycznie.

Ponieważ obie zmienne fikcyjne nie były istotne statystycznie, mogliśmy usunąć z modelu stan cywilny jako czynnik predykcyjny, ponieważ nie wydaje się, aby zwiększał on wartość predykcyjną dochodu.

Dodatkowe zasoby

Zmienne jakościowe i ilościowe
Sztuczna pułapka zmienna
Jak czytać i interpretować tabelę regresji
Wyjaśnienie wartości P i istotności statystycznej