Zmienne instrumentalne: definicja i przykłady

Często w statystyce staramy się oszacować wpływ jednej zmiennej na drugą. Na przykład możemy chcieć wiedzieć:

• Jak czas spędzony na nauce wpływa na wyniki egzaminów?
• Jak dany lek wpływa na ciśnienie krwi?
• Jak stres wpływa na tętno?

W każdym scenariuszu chcemy zrozumieć, czy zmienna predykcyjna wpływa na zmienną odpowiedzi . Często jednak istnieją inne zmienne, które wpływają na związek między tymi dwiema zmiennymi.

Załóżmy na przykład, że używamy określonego leku jako zmiennej predykcyjnej, a ciśnienie krwi jako zmiennej odpowiedzi. Interesuje nas tylko wpływ leku na ciśnienie krwi:

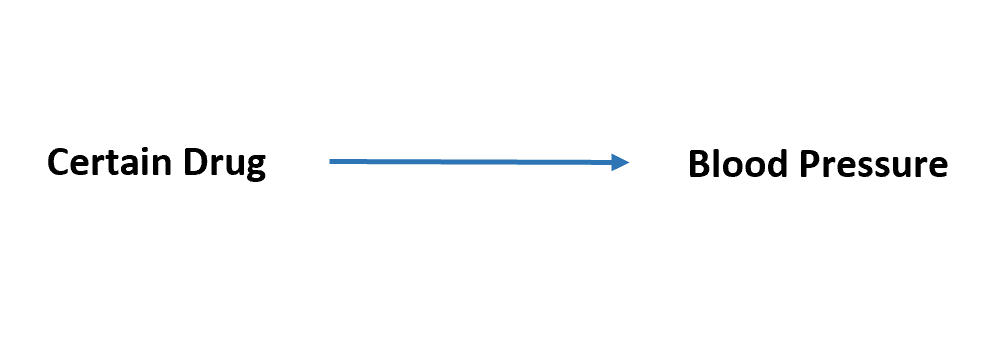
Jednak inne zmienne, takie jak czas spędzony na ćwiczeniach, ogólna dieta i poziom stresu również wpływają na ciśnienie krwi:

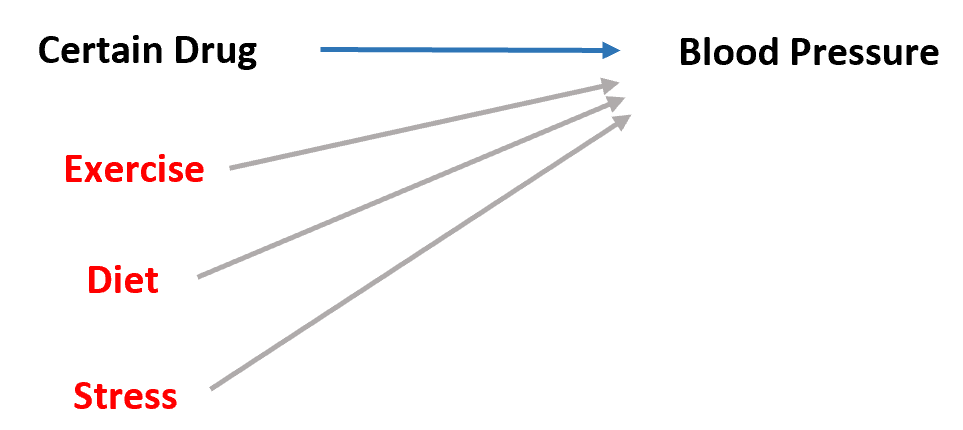
Tak więc, jeśli przeprowadzimy prostą regresję liniową , stosując lek jako zmienną predykcyjną i ciśnienie krwi jako zmienną odpowiedzi, nie możemy być pewni, że współczynniki regresji dokładnie oddają wpływ leku na ciśnienie krwi, ponieważ czynniki zewnętrzne (ćwiczenia, dieta, stres itp.) również mogą odgrywać rolę.

Jednym z potencjalnych sposobów obejścia tego problemu jest użycie zmiennej instrumentalnej .

Co to jest zmienna instrumentalna?

Zmienna instrumentalna to trzecia zmienna wprowadzona do analizy regresji, która jest skorelowana ze zmienną predykcyjną, ale nieskorelowana ze zmienną odpowiedzi. Używając tej zmiennej, możliwe staje się oszacowanie prawdziwego efektu przyczynowego, jaki zmienna predykcyjna wywiera na zmienną odpowiedzi.

Załóżmy na przykład, że chcemy oszacować wpływ określonego leku na ciśnienie krwi:

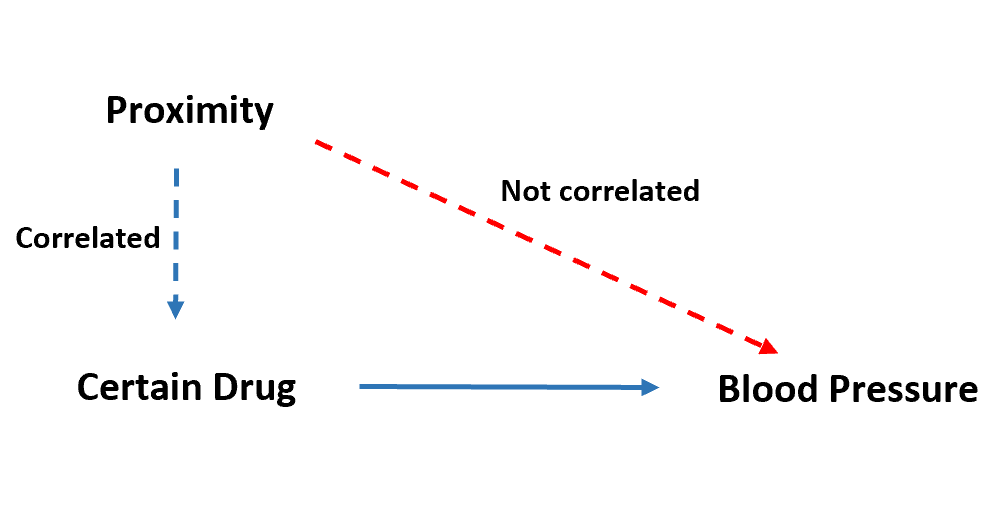
Przykładem zmiennej instrumentalnej, którą możemy wykorzystać w tej analizie regresji, jest bliskość apteki.

Ta zmienna „bliskości” byłaby prawdopodobnie silnie skorelowana z tym, czy dana osoba przyjmuje dany lek, czy nie, ponieważ osoba ta nie byłaby w stanie go uzyskać, jeśli nie mieszkałaby w pobliżu apteki.

Jednakże zmienna „bliskości” nie powinna mieć żadnej korelacji z ciśnieniem krwi. Jedynym powiązaniem tego zjawiska z ciśnieniem krwi jest zmienna predykcyjna.

Sposób, w jaki faktycznie używamy zmiennej instrumentalnej, polega na przeprowadzeniu regresji zmiennej instrumentalnej, czasami nazywanej dwuetapową regresją najmniejszych kwadratów .

Regresja zmiennych instrumentalnych

Regresja zmiennych instrumentalnych (lub dwustopniowa regresja metodą najmniejszych kwadratów) wykorzystuje następujące podejście do oszacowania wpływu zmiennej predykcyjnej na zmienną odpowiedzi:

Krok 1: Dopasuj model regresji, używając zmiennej instrumentalnej jako zmiennej predykcyjnej.

W naszym konkretnym przykładzie najpierw dopasujemy następujący model regresji:

Niektóre leki = B ₀ + B ₁ (bliskość)

Pozostałyby nam przewidywane wartości dla niektórych leków (cd), które nazwiemy cd _hat .

Krok 2: Dopasuj drugi model regresji, korzystając z przewidywanych wartości dla cd _hat .

Następnie dopasujemy następujący model regresji:

Ciśnienie krwi = B ₀ + B ₁ (cd _hat )

Jeśli okaże się, że współczynnik regresji cd _hat jest statystycznie istotny, to można powiedzieć, że lek ma przyczynowy wpływ na ciśnienie krwi.

Powodem, dla którego możemy to powiedzieć, jest to, że przy tworzeniu CD _Hat użyliśmy jedynie terminu „bliskość” i wiemy, że bliskość nie powinna być korelowana z ciśnieniem krwi, jakąkolwiek istotną korelację w regresji drugiego etapu można przypisać określonemu lekowi.

Środki ostrożności dotyczące stosowania zmiennych instrumentalnych

Zmienna instrumentalna powinna być stosowana tylko wtedy, gdy spełnia następujące kryteria:

• Jest ona silnie skorelowana ze zmienną predykcyjną.
• Nie jest ona skorelowana ze zmienną odpowiedzi.
• Nie jest ona skorelowana z innymi zmiennymi wyłączonymi z modelu (np. bliskość nie jest skorelowana z ćwiczeniami, dietą czy stresem).

Jeżeli zmienna instrumentalna nie spełnia tego kryterium, nie powinna być stosowana w modelu regresji, ponieważ prawdopodobnie doprowadzi do niewiarygodnych i stronniczych wyników.