Co to są zmienne losowe?

Zmienna losowa , ogólnie oznaczana jako X, to zmienna, której możliwe wartości są wynikami procesu losowego.

Istnieją dwa rodzaje zmiennych losowych: dyskretne i ciągłe .

Dyskretne zmienne losowe

Dyskretna zmienna losowa to taka, która może przyjmować tylko policzalną liczbę różnych wartości, takich jak 0, 1, 2, 3, 4, 5…100, 1 milion itd. Oto kilka przykładów dyskretnych zmiennych losowych:

• Ile razy moneta wyrzuci reszkę po 20-krotnym rzucie.
• Liczba przypadków, w których kość ląduje na liczbie 4 po rzucie 100 razy.
• Liczba wadliwych widżetów w pudełku zawierającym 50 widżetów.

Rozkład prawdopodobieństwa dyskretnej zmiennej losowej mówi nam, jakie jest prawdopodobieństwo, że zmienna losowa przyjmie określone wartości.

Załóżmy na przykład, że rzucamy raz uczciwą kostką. Jeśli pozwolimy, aby X oznaczało prawdopodobieństwo, że kość wypadnie na określoną liczbę, wówczas rozkład prawdopodobieństwa można zapisać w następujący sposób:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Notatka:

Aby rozkład prawdopodobieństwa był ważny, musi spełniać dwa następujące kryteria:

1. Prawdopodobieństwo każdego wyniku musi mieścić się w przedziale od 0 do 1.

2. Suma wszystkich prawdopodobieństw musi wynosić 1.

Należy zauważyć, że rozkład prawdopodobieństwa rzutu kostką spełnia oba te kryteria:

1. Prawdopodobieństwo każdego wyniku wynosi od 0 do 1.

2. Suma wszystkich prawdopodobieństw sumuje się do 1.

Możemy użyć histogramu do wizualizacji rozkładu prawdopodobieństwa:

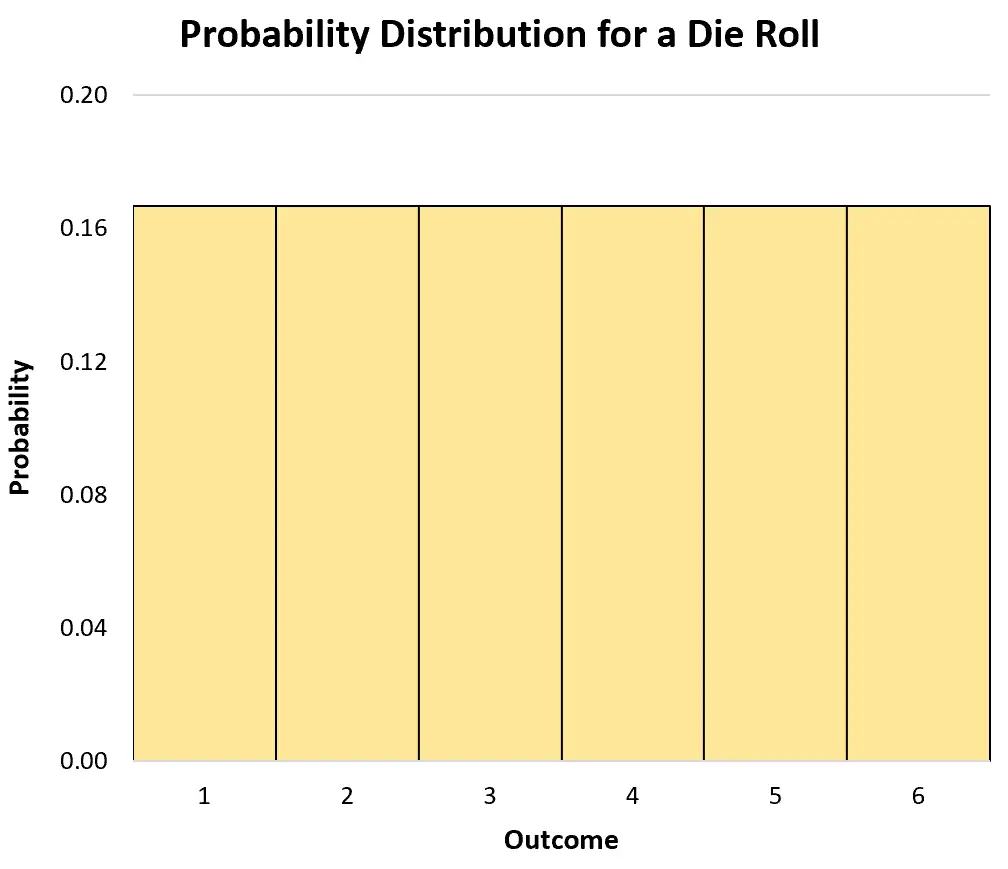
Skumulowany rozkład prawdopodobieństwa dyskretnej zmiennej losowej informuje nas o prawdopodobieństwie, że zmienna przyjmie wartość równą lub mniejszą od określonej wartości.

Na przykład skumulowany rozkład prawdopodobieństwa rzutu kostką będzie wyglądał następująco:

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

Szansa, że kość wyląduje na jednej lub mniejszej liczbie, wynosi po prostu 1/6, ponieważ kość nie może wylądować na liczbie mniejszej niż jeden.

Prawdopodobieństwo, że wyląduje na dwóch lub mniej, wynosi P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

Podobnie prawdopodobieństwo, że wyląduje na trójce lub mniej, wynosi P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6, oraz Wkrótce.

Możemy również użyć histogramu do wizualizacji skumulowanego rozkładu prawdopodobieństwa:

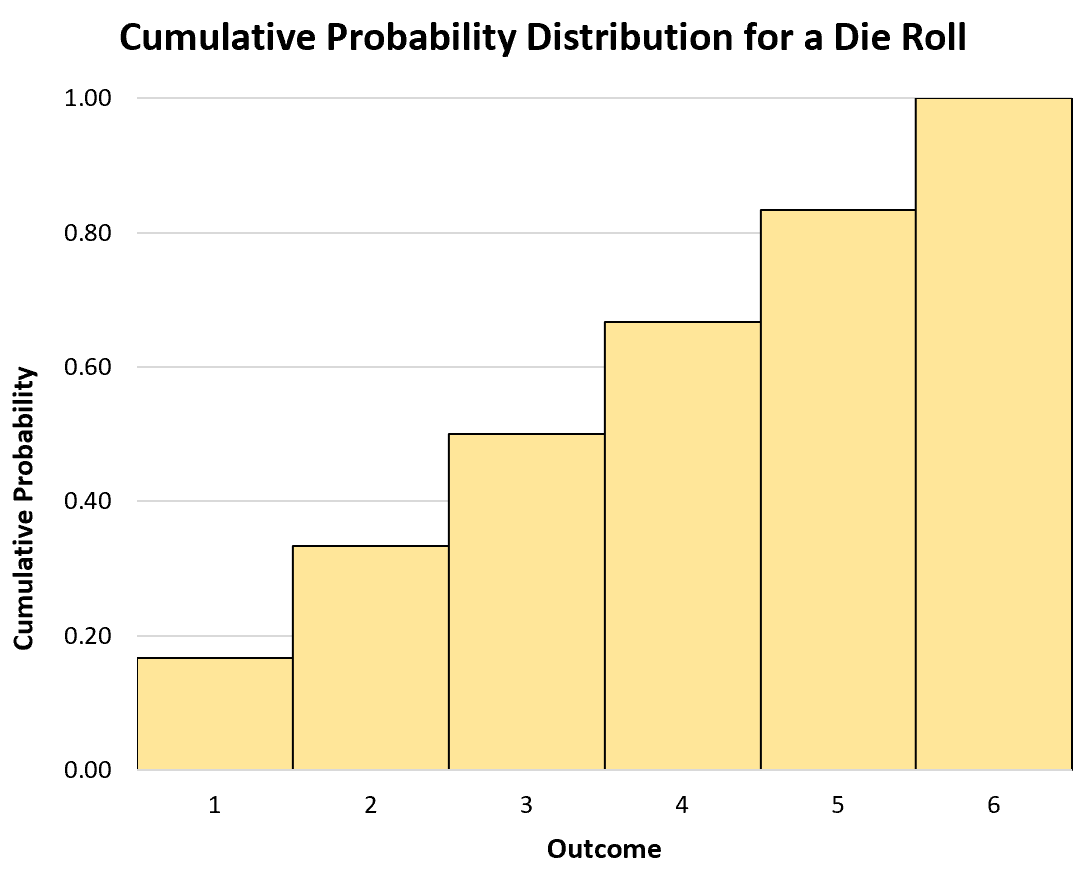
Ciągłe zmienne losowe

Ciągła zmienna losowa to zmienna, która może przyjmować nieskończenie wiele możliwych wartości. Oto kilka przykładów ciągłych zmiennych losowych:

• Waga zwierzęcia
• Wysokość osoby
• Czas potrzebny na przebiegnięcie maratonu

Na przykład wzrost osoby może wynosić 60,2 cala, 65,2344 cala, 70,431222 cala itd. Istnieje nieskończona liczba możliwych wartości rozmiaru.

Główna zasada:

Jeśli możesz policzyć liczbę wyników, to pracujesz z dyskretną zmienną losową – na przykład licząc, ile razy moneta wypadnie reszką.

Ale jeśli możesz zmierzyć wynik, pracujesz z ciągłą zmienną losową – na przykład mierząc wzrost, wagę, czas itp.

Rozkład prawdopodobieństwa ciągłej zmiennej losowej mówi nam, jakie jest prawdopodobieństwo, że zmienna losowa przyjmie określone wartości.

Jednakże w przeciwieństwie do rozkładu prawdopodobieństwa dyskretnych zmiennych losowych, rozkład prawdopodobieństwa ciągłej zmiennej losowej można wykorzystać jedynie do określenia prawdopodobieństwa, że zmienna przyjmie określony zakres wartości.

Załóżmy na przykład, że chcemy poznać prawdopodobieństwo, że hamburger z określonej restauracji waży ćwierć funta (0,25 funta). Ponieważ waga jest zmienną ciągłą, może przyjmować nieskończoną liczbę wartości.

Na przykład dany hamburger może w rzeczywistości ważyć 0,250001 funta, czyli 0,24 funta, czyli 0,2488 funta. Prawdopodobieństwo, że dany hamburger będzie ważył dokładnie 0,25 funta, wynosi w zasadzie zero.

Możemy zatem użyć rozkładu prawdopodobieństwa, aby określić prawdopodobieństwo, że hamburger waży mniej niż 0,25 funta, więcej niż 0,25 funta lub mieści się w pewnym zakresie (np. od 0,23 funta do 0,27 funta).

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji na temat zmiennych losowych:

Co to są zmienne losowe iid?
10 przykładów zmiennych losowych w prawdziwym życiu