Zmienność

Przez Benjamin Anderson 5 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniamy, czym jest wariancja, zwana także wariancją, i jak jest obliczana. Znajdziesz tu wzór na wariancję, konkretny przykład obliczania wariancji, a dodatkowo będziesz mógł obliczyć wariancję dowolnego zbioru danych za pomocą kalkulatora online.

Pokazujemy również, jak znaleźć wariancję zgrupowanych danych, ponieważ odbywa się to w inny sposób. Na koniec nauczymy Cię różnicy między wariancją populacji a wariancją próbki, różnicy między wariancją a odchyleniem standardowym oraz właściwości tej miary statystycznej.

Co to jest wariancja?

W statystyce wariancja jest miarą rozproszenia, która wskazuje zmienność zmiennej losowej. Wariancja jest równa sumie kwadratów reszt podzielonej przez całkowitą liczbę obserwacji.

Należy pamiętać, że resztę rozumie się jako różnicę między wartością punktu danych statystycznych a średnią zbioru danych.

W teorii prawdopodobieństwa symbolem wariancji jest grecka litera sigma do kwadratu (σ ² ). Chociaż jest on również zwykle przedstawiany jako Var(X) , gdzie X jest zmienną losową, na podstawie której obliczana jest wariancja.

Ogólnie rzecz biorąc, interpretacja wartości wariancji zmiennej losowej jest prosta. Im większa wartość wariancji, tym bardziej rozproszone są dane. I odwrotnie, im mniejsza wartość wariancji, tym mniejsze rozproszenie będzie w seriach danych. Jednak interpretując wariancję, należy uważać na wartości odstające , ponieważ mogą one zafałszować wartość wariancji.

wariancji, inne miary uważane poza rozproszeniem to rozstęp, odchylenie standardowe, odchylenie średnie i współczynnik zmienności.

Jak obliczyć różnicę

Aby obliczyć wariancję, należy wykonać następujące kroki:

Znajdź średnią arytmetyczną zbioru danych.
Oblicz reszty, zdefiniowane jako różnica między wartościami a średnią zbioru danych.
Każdą resztę podnieś do kwadratu.
Dodaj wszystkie wyniki obliczone w poprzednim kroku.
Podziel przez całkowitą liczbę danych. Otrzymany wynik jest wariancją serii danych.

Podsumowując, wzór na obliczenie wariancji zbioru danych jest następujący:

Złoto:

$X$

jest zmienną losową, dla której chcesz obliczyć wariancję.
$x_i$

jest wartością danych

$i$

.
$n$

to całkowita liczba obserwacji.
$\overline{X}$

jest średnią zmiennej losowej

$X$

.

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć wariancję dowolnego zbioru danych.

Dlatego też, aby wyodrębnić wariancję z serii danych, niezbędna jest wiedza, w jaki sposób obliczana jest średnia arytmetyczna. Jeśli nie pamiętasz, jak to zrobić, możesz to sprawdzić w artykule, do którego link znajduje się powyżej.

Przykład odchylenia

Teraz, gdy znamy definicję wariancji, rozwiążemy ćwiczenie krok po kroku, abyś mógł zobaczyć, jak uzyskuje się wariancję serii danych.

Z międzynarodowej firmy znany jest wynik ekonomiczny, jaki osiągnęła w ciągu ostatnich pięciu lat, w większości osiągnęła zyski, ale w jednym roku wykazała znaczne straty: 11,5, 2, -9, 7 mln euro. Oblicz wariancję tego zbioru danych.

Jak widzieliśmy w powyższym wyjaśnieniu, pierwszą rzeczą, którą musimy zrobić, aby znaleźć wariancję serii danych, jest obliczenie jej średniej arytmetycznej:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

Kiedy już znamy średnią wartość danych, możemy skorzystać ze wzoru na wariancję:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

Dane podane w zestawieniu ćwiczeń podstawiamy do wzoru:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

Na koniec pozostaje tylko rozwiązać operacje obliczające wariancję:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

Należy zauważyć, że jednostki wariancji to te same jednostki danych statystycznych, ale podniesione do kwadratu, dlatego wariancja tej grupy danych wynosi 45,76 mln euro ² .

Kalkulator luki

Wprowadź zestaw danych statystycznych do poniższego kalkulatora, aby obliczyć jego wariancję. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Wariancja dla danych pogrupowanych

Aby obliczyć wariancję danych pogrupowanych w przedziały , należy wykonać następujące kroki:

Znajdź średnią zgrupowanych danych.
Oblicz reszty zgrupowanych danych.
Każdą resztę podnieś do kwadratu.
Pomnóż każdy poprzedni wynik przez częstotliwość jego przedziału.
Dodaj sumę wszystkich wartości uzyskanych w poprzednim kroku.
Podziel przez całkowitą liczbę obserwacji. Wynikowa liczba jest wariancją pogrupowanych danych.

Innymi słowy, wzór na obliczenie wariancji danych pogrupowanych w przedziały jest następujący:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

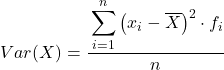
Chociaż powyższy wzór jest zwykle używany, poniższe wyrażenie algebraiczne może być również użyte, ponieważ jest równoważne:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

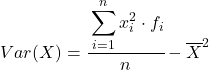
Jako przykład znajdziemy wariancję następujących pogrupowanych serii danych:

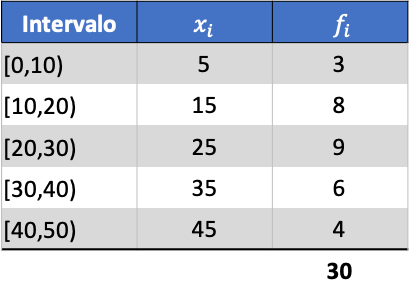
Najpierw musimy wyznaczyć średnią z pogrupowanych danych. W tym celu dodajemy w tabeli częstotliwości kolumnę zawierającą iloczyn znaku klasy i częstotliwości:

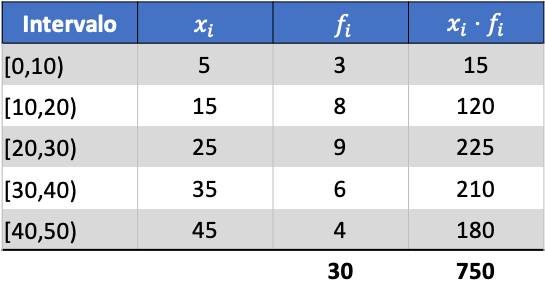
Teraz obliczamy średnią z pogrupowanych danych, dzieląc sumę dodanej kolumny przez całkowitą liczbę danych:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

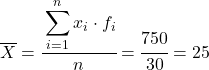
A ze średniej obliczonych danych możemy dodać następujące trzy kolumny:

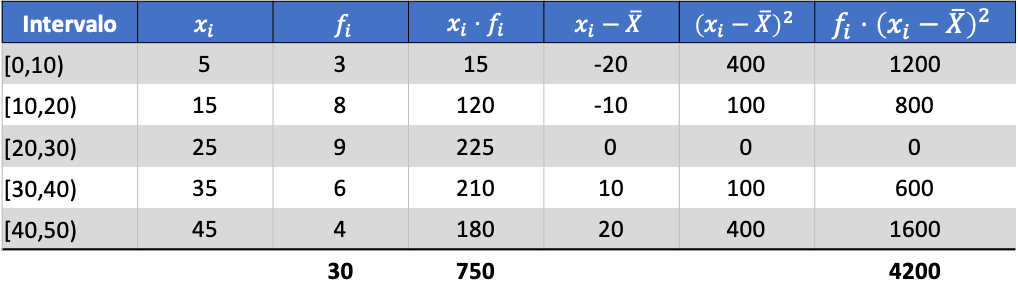
Zatem wariancja zbiorczego zbioru danych jest sumą ostatniej kolumny podzieloną przez całkowitą liczbę zaobserwowanych danych:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

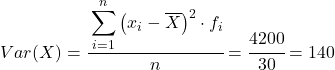
Wariancja i odchylenie standardowe

Wariancja i odchylenie standardowe (lub odchylenie standardowe) to dwie miary rozproszenia i dlatego obie wskazują stopień rozproszenia zbioru danych. Jednak różnica między wariancją a odchyleniem standardowym polega na tym, że generalnie wariancja ma większe wartości, ponieważ jest kwadratem odchylenia standardowego.

Odchylenie standardowe jest zazwyczaj oznaczane grecką literą sigma (σ) i z tego powodu wariancję oznacza się literą sigma kwadrat (σ ² ), ponieważ jest to matematyczna zależność istniejąca pomiędzy tymi dwoma metrykami dyspersji.

$Var(X)=\sigma^2$

Zatem po obliczeniu wartości wariancji zbioru danych można łatwo znaleźć wartość odchylenia standardowego tego samego zbioru, po prostu biorąc pierwiastek kwadratowy z wariancji.

$\sigma=\sqrt{\sigma^2}$

Wariancja populacji i wariancja próby

Logicznie rzecz biorąc, wariancja populacji odnosi się do obliczenia wariancji populacji statystycznej i zamiast tego wariancja próbki jest stosowana do obliczenia wariancji próbki. Są to jednak dwie różne koncepcje, ponieważ wzór na wariancję populacji różni się od wzoru na wariancję próbki.

Zwykle w ćwiczeniach wariancyjnych, jeśli nie mówią nam inaczej, aby znaleźć wariancję podanego zbioru danych, musimy skorzystać ze wzoru na wariancję populacji , czyli tego, który wyjaśniliśmy na początku artykułu:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

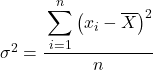
Być może jednak w przypadku niektórych problemów zostaniesz poproszony o potraktowanie danych statystycznych jako próbki, w takim przypadku musimy skorzystać ze wzoru na wariancję próbki :

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

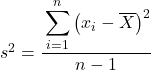
Należy zauważyć, że aby wskazać, że obliczana jest wariancja populacji, jest ona oznaczona grecką literą σ, ale gdy obliczana jest wariancja próbki, używana jest litera s.

Jak widać, jedyną różnicą między tymi dwoma wzorami jest to, że wariancję próbki musimy podzielić przez całkowitą liczbę obserwacji minus 1, na przykład, jeśli w sumie jest 30 elementów danych, podzielimy przez 29 Ale obliczenie licznika odbywa się dokładnie w ten sam sposób.

Właściwości wariancyjne

Wariancja ma następujące właściwości:

Wariancja dowolnej zmiennej losowej będzie zawsze większa lub równa zero. Podobnie, jeśli wariancja wynosi zero, oznacza to, że wszystkie dane statystyczne są takie same.

$Var(x)\ge 0$

Oczywiście wariancja pojedynczej wartości wynosi zero.

$Var(a)=0\qquad a\in \mathbb{R}$

Wariancja iloczynu skalara przez zmienną jest równa kwadratowi skalara razy wariancja zmiennej.

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

Wariancja sumy dwóch zmiennych zależnych jest równa sumie wariancji każdej zmiennej z osobna plus dwukrotność kowariancji między dwiema zmiennymi.

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

W konsekwencji, jeżeli obie zmienne są niezależne, to aby wyznaczyć wariancję ich sumy, wystarczy dodać ich wariancje:

$Var(X+Y)=Var(X)+Var(Y)$

Odchylenie można również określić za pomocą oczekiwań matematycznych, korzystając z następującego wzoru:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej