Dlaczego średnia jest ważna w statystyce?

Średnia zbioru danych reprezentuje średnią wartość zbioru danych. Oblicza się go w następujący sposób:

Średnia = Σx _i /n

Złoto:

• Σ: Symbol oznaczający „sumę”
• x _i : i ^-ta obserwacja w zbiorze danych
• n: całkowita liczba obserwacji w zbiorze danych

Załóżmy na przykład, że mamy następujący zbiór danych zawierający 11 obserwacji:

Zbiór danych: 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17

Średnią ze zbioru danych oblicza się w następujący sposób:

Średnia = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9,54

W statystyce średnia jest ważna z następujących powodów:

1. Średnia daje nam wyobrażenie o tym, gdzie znajduje się „środek” zbioru danych.

2. Ze względu na sposób obliczania średnia zawiera w zbiorze danych informacje z każdej obserwacji .

Poniższy przykład ilustruje te dwa powody.

Przykład: Oblicz średnią zbioru danych

Załóżmy, że mamy zbiór danych zawierający ceny sprzedaży 10 000 różnych domów w określonym mieście.

Zamiast patrzeć na tysiące wierszy surowych danych , możemy obliczyć średnią wartość, aby szybko poznać średnią cenę sprzedaży domów w danym mieście.

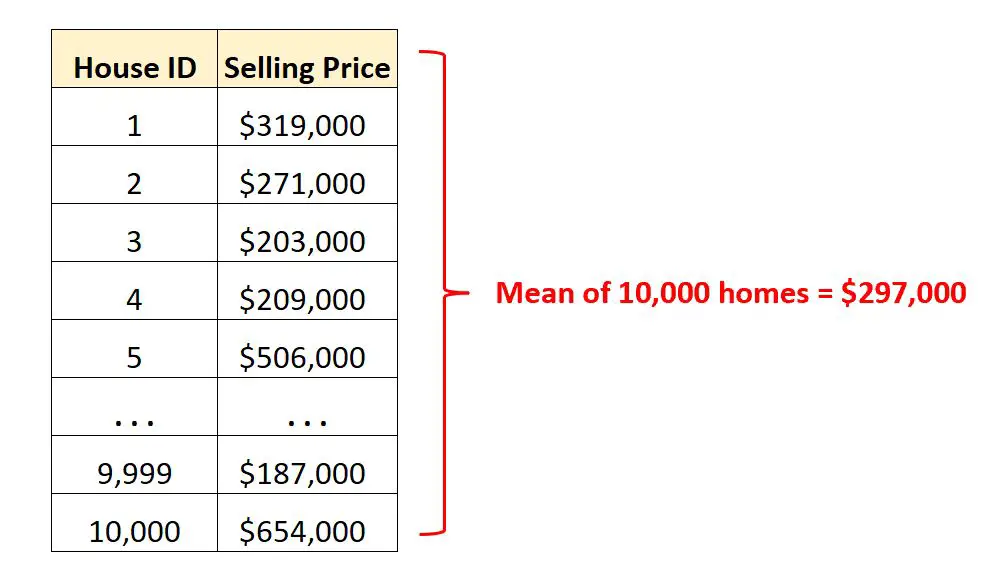
Świadomość, że średnia cena sprzedaży wynosi 297 000 dolarów, daje nam wyobrażenie o tym, za ile sprzedaje się „typowy” dom w tym mieście.

Ta pojedyncza wartość średniej jest znacznie łatwiejsza do zinterpretowania niż przeglądanie wszystkich wierszy surowych danych.

A ponieważ do obliczenia średniej wykorzystano cenę sprzedaży każdego domu, mogliśmy pomnożyć średnią cenę sprzedaży przez całkowitą liczbę domów, aby znaleźć całkowitą cenę sprzedaży wszystkich domów w tym mieście:

• Całkowita cena sprzedaży wszystkich domów = Średnia cena sprzedaży * Liczba domów
• Całkowita cena sprzedaży wszystkich domów = 297 000 USD * 10 000
• Całkowita cena sprzedaży wszystkich domów = 2 970 000 000 dolarów

Widzimy, że łączna cena sprzedaży wszystkich domów w tym mieście wynosi 2,97 miliarda dolarów.

Kiedy stosować średnią

Analizując zbiory danych, często chcemy zrozumieć, gdzie leży główna wartość.

W statystyce istnieją dwie popularne metryki, których używamy do pomiaru środka zbioru danych:

• Średnia : średnia wartość w zestawie danych
• Mediana : mediana wartości w zestawie danych

Średnia jest najczęstszym sposobem pomiaru środka zbioru danych, ale w rzeczywistości może wprowadzać w błąd w następujących sytuacjach:

• Gdy rozkład jest asymetryczny .
• Gdy rozkład zawiera wartości odstające .

Aby to zilustrować, rozważmy dwa poniższe przykłady.

Przykład 1: Obliczanie średniej rozkładu skośnego

Rozważmy następujący rozkład wynagrodzeń mieszkańców danego miasta:

Wysokie płace po prawej stronie rozkładu wypychają średnią z centrum rozkładu.

Zatem mediana lepiej odzwierciedla „typową” pensję mieszkańca niż średnia, ponieważ rozkład jest przesunięty w prawo.

W tym konkretnym przykładzie średnia pensja wynosi 47 000 dolarów, podczas gdy mediana wynagrodzenia wynosi 32 000 dolarów.

Zatem mediana jest znacznie bardziej reprezentatywna dla typowego wynagrodzenia w tym mieście.

Przykład 2: Obliczanie średniej w obecności wartości odstających

Rozważmy następujący wykres przedstawiający powierzchnię domów przy określonej ulicy:

Na średnią duży wpływ ma kilka niezwykle dużych domów, podczas gdy na medianę nie.

Widzimy, że mediana lepiej oddaje „typową” powierzchnię domu przy tej ulicy niż średnia, ponieważ nie mają na nią wpływu wartości odstające.

Streszczenie

Oto krótkie podsumowanie głównych wniosków z tego artykułu:

• Średnia reprezentuje średnią wartość w zestawie danych.
• Średnia jest ważna, ponieważ daje nam wyobrażenie o tym, gdzie w zbiorze danych znajduje się wartość środkowa.
• Średnia jest również ważna, ponieważ zawiera informacje z każdej obserwacji w zbiorze danych.
• Średnia może wprowadzać w błąd, jeśli zbiór danych jest wypaczony lub zawiera wartości odstające. W tych scenariuszach mediana daje dokładniejsze wyobrażenie o tym, gdzie znajduje się „środek” zbioru danych.

Dodatkowe zasoby

Poniższe samouczki dostarczają dodatkowych informacji na temat innych statystyk opisowych:

Dlaczego mediana jest ważna w statystyce?
Dlaczego odchylenie standardowe jest ważne w statystyce?
Kiedy stosować średnią a kiedy medianę