Jak znaleźć równanie regresji liniowej z tabeli

Często możesz chcieć znaleźć równanie regresji liniowej w tabeli danych.

Załóżmy na przykład, że otrzymasz następującą tabelę danych:

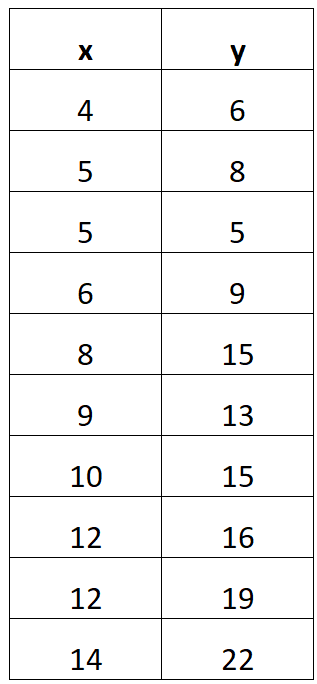
Poniższy przykład pokazuje krok po kroku, jak znaleźć równanie regresji liniowej na podstawie tej tabeli danych.

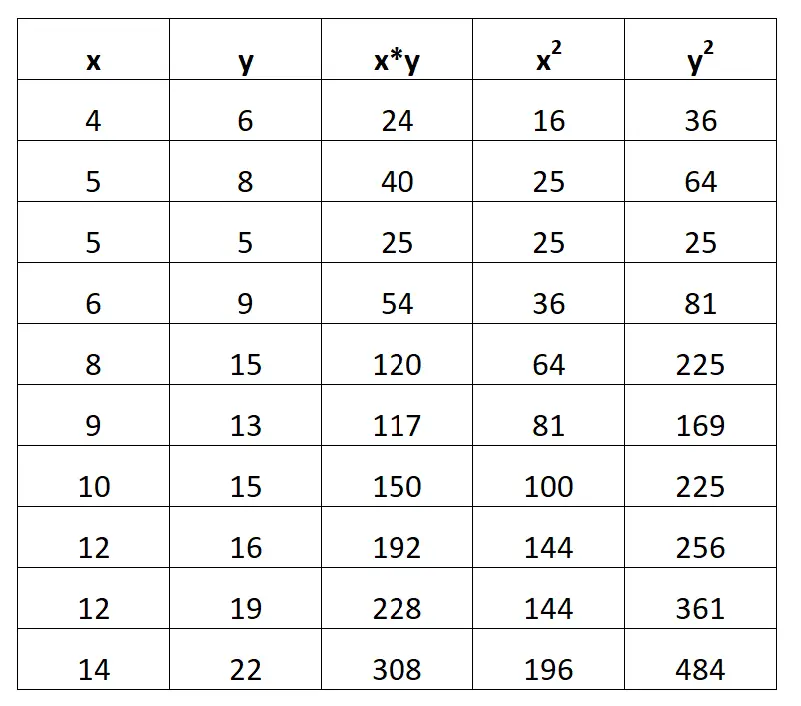
Krok 1: Oblicz X*Y, ^X2 i ^Y2

Najpierw obliczymy następujące dane dla każdego wiersza:

• x*y
• ^x2
• i ²

Poniższy zrzut ekranu pokazuje, jak to zrobić:

Krok 2: Oblicz ΣX, ΣY, ΣX*Y, ΣX ² i ΣY ²

Następnie obliczymy sumę każdej kolumny:

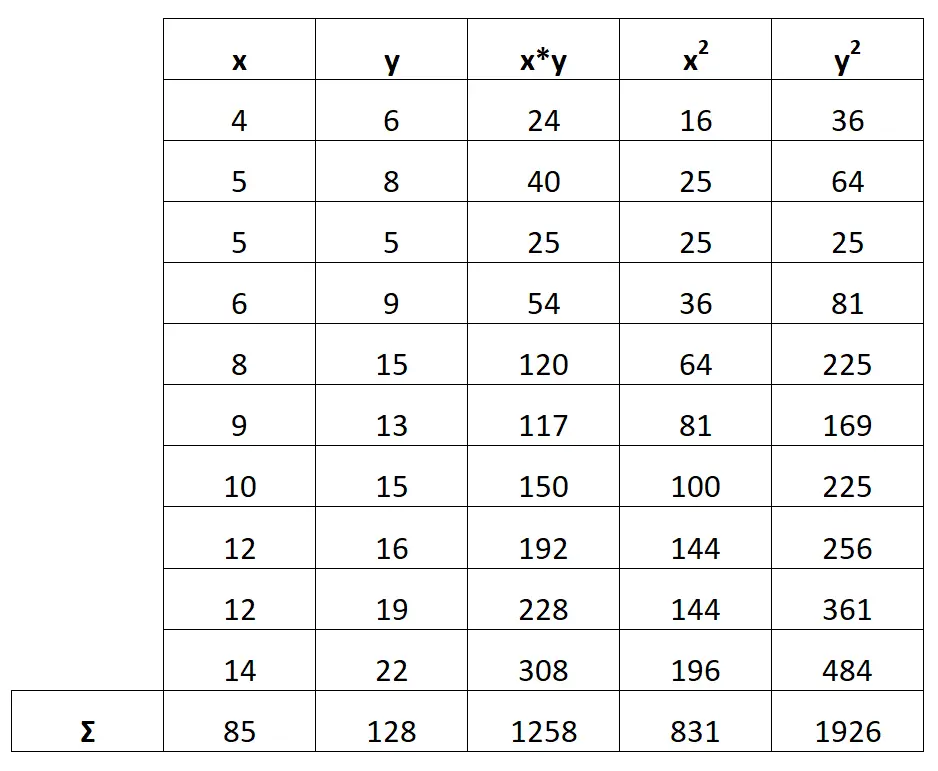
Krok 3: Oblicz b ₀

Wzór na obliczenie wyrazu wolnego równania regresji b ₀ jest następujący:

• b ₀ = ((Σy)(Σx ² ) – (Σx)(Σxy)) / (n(Σx ² ) – (Σx) ² )
• b ₀ = ((128)(831) – (85)(1258)) / (10(831) – (85) ² )
• _b0 = -0,518

Uwaga : we wzorze n oznacza całkowitą liczbę obserwacji. W tym przykładzie było łącznie 10 obserwacji.

Krok 4: Oblicz b ₁

Wzór na obliczenie nachylenia równania regresji b ₁ jest następujący:

• b ₁ = (n(Σxy) – (Σx)(Σy)) / (n(Σx ² ) – (Σx) ² )
• b ₁ = (10(1258) – (85)(128)) / (10(831) – (85) ² )
• _b1 = 1,5668

Krok 5: Napisz równanie regresji liniowej

Ostateczne równanie regresji liniowej można zapisać jako:

• ŷ = b ₀ + b ₁ x

Zatem nasze równanie regresji liniowej można zapisać w następujący sposób:

• ŷ = -0,518 + 1,5668x

Poprawność tej odpowiedzi możemy sprawdzić wstawiając wartości z tabeli do prostego kalkulatora regresji liniowej :

Widzimy, że równanie regresji liniowej z kalkulatora odpowiada równaniu, które obliczyliśmy ręcznie.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat regresji liniowej:

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Jak interpretować współczynniki regresji