Como realizar o teste de tukey em r
Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.
Se o valor p geral da tabela ANOVA estiver abaixo de um certo nível de significância, então temos evidências suficientes para dizer que pelo menos uma das médias do grupo é diferente das outras.
No entanto, isso não nos diz quais grupos são diferentes uns dos outros. Isto simplesmente nos diz que nem todas as médias dos grupos são iguais. Para saber exatamente quais grupos são diferentes entre si, precisamos realizar um teste post hoc .
Um dos testes post hoc mais comumente usados é o teste de Tukey , que nos permite realizar comparações pareadas entre as médias de cada grupo enquanto controlamos a taxa de erro familiar .
Este tutorial explica como realizar o teste de Tukey em R.
Nota: Se algum dos grupos do seu estudo for considerado um grupo de controle, você deverá usar o teste de Dunnett como teste post-hoc.
Exemplo: teste de Tukey em R
Etapa 1: ajuste o modelo ANOVA.
O código a seguir mostra como criar um conjunto de dados falso com três grupos (A, B e C) e ajustar um modelo ANOVA unidirecional aos dados para determinar se os valores médios de cada grupo são iguais:
#make this example reproducible set.seed(0) #create data data <- data.frame(group = rep (c("A", "B", "C"), each = 30), values = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data head(data) group values 1 A 2.6900916 2 A 0.7965260 3 A 1.1163717 4 A 1.7185601 5 A 2.7246234 6 A 0.6050458 #fit one-way ANOVA model model <- aov (values~group, data=data) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) group 2 98.93 49.46 30.83 7.55e-11 *** Residuals 87 139.57 1.60 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Podemos ver que o valor p geral da tabela ANOVA é 7,55e-11 . Como esse número é inferior a 0,05, temos evidências suficientes para afirmar que os valores médios de cada grupo não são iguais. Portanto, podemos fazer o teste de Tukey para determinar exatamente quais médias de grupo são diferentes.
Passo 2: Realize o teste de Tukey.
O código a seguir mostra como usar a função TukeyHSD() para realizar o teste de Tukey:
#perform Tukey's Test TukeyHSD(model, conf.level= .95 ) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = values ~ group, data = data) $group diff lwr upr p adj BA 0.9777414 0.1979466 1.757536 0.0100545 CA 2.5454024 1.7656076 3.325197 0.0000000 CB 1.5676610 0.7878662 2.347456 0.0000199
O valor p indica se há ou não diferença estatisticamente significativa entre cada programa. Os resultados mostram que existe diferença estatisticamente significativa entre a perda média de peso de cada programa no nível de significância de 0,05.
Especialmente:
- Valor P para a diferença de médias entre B e A: 0,0100545
- Valor P para a diferença de médias entre C e A: 0,0000000
- Valor P para a diferença de médias entre C e B: 0,0000199
Etapa 3: visualize os resultados.
Também podemos usar a função plot(TukeyHSD()) para visualizar intervalos de confiança:
#plot confidence intervals plot(TukeyHSD(model, conf.level= .95 ), las = 2 )
Nota: O argumento las especifica que os rótulos de escala devem ser perpendiculares (las=2) ao eixo.
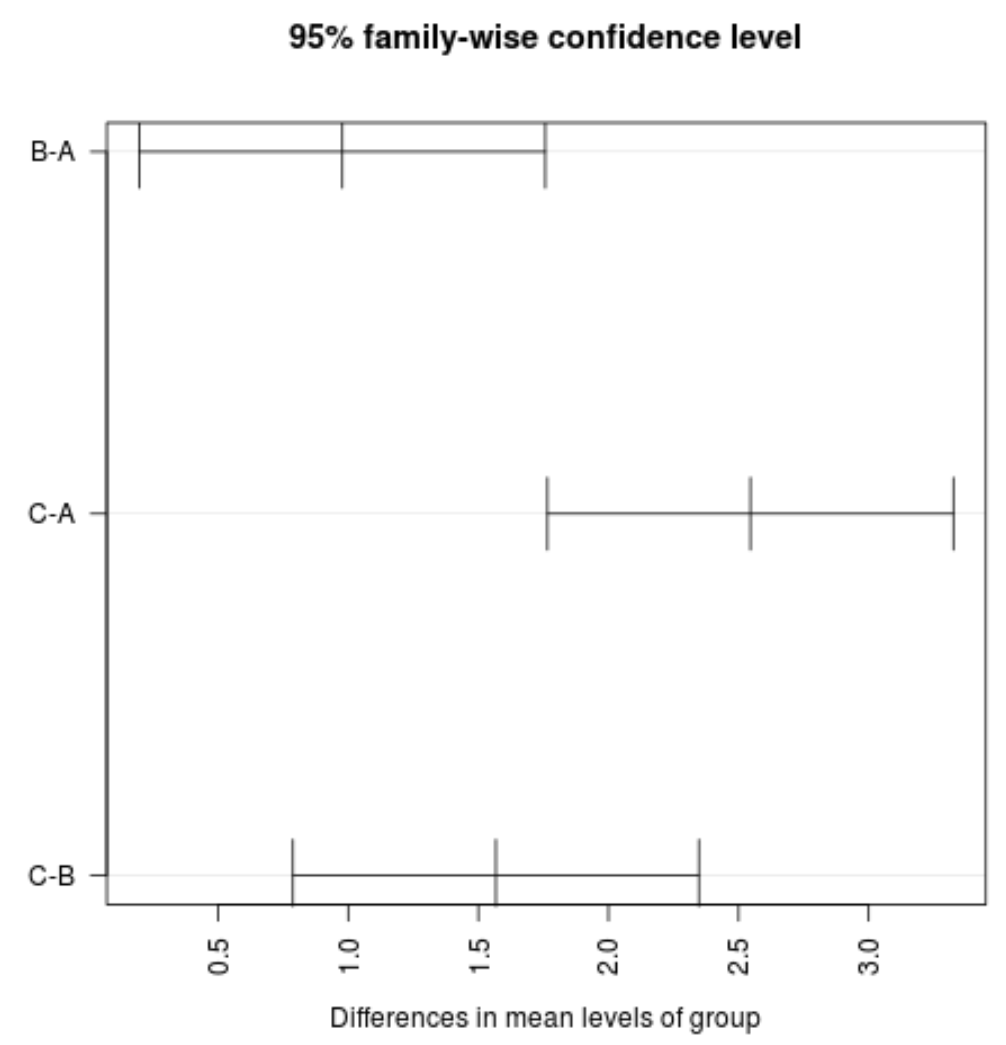
Podemos perceber que nenhum dos intervalos de confiança para o valor médio entre os grupos contém o valor zero, indicando que há diferença estatisticamente significativa na perda média entre os três grupos. Isso é consistente com todos os valores de p para nossos testes de hipótese sendo inferiores a 0,05.
Para este exemplo específico, podemos concluir o seguinte:
- Os valores médios do grupo C são significativamente superiores aos valores médios dos grupos A e B.
- Os valores médios do grupo B são significativamente superiores aos valores médios do grupo A.
Recursos adicionais
Um guia para usar testes post-hoc com ANOVA
Como realizar ANOVA unidirecional em R
Como realizar ANOVA bidirecional em R