Critério chauvenet: definição e exemplo

Um outlier é uma observação anormalmente distante de outros valores em um conjunto de dados. Valores discrepantes podem ser problemáticos porque podem afetar os resultados de uma análise.

Uma forma de identificar outliers em um conjunto de dados é utilizar o critério de Chauvenet , que utiliza o seguinte processo:

1. Para cada valor individual x _i no conjunto de dados, calcule o desvio da média da seguinte forma:

Desvio = |x _i – x | /s

onde x é a média amostral e s é o desvio padrão amostral.

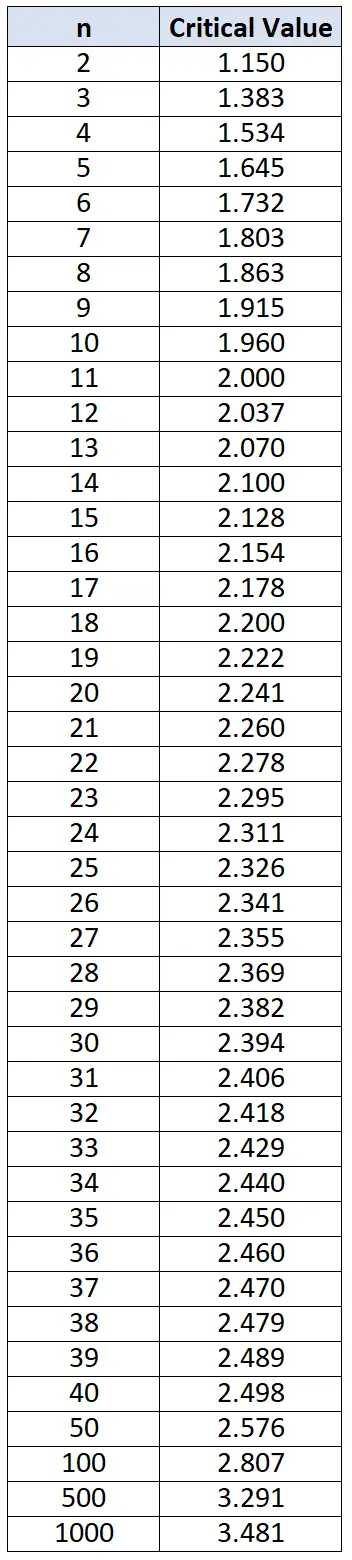
2. Compare os desvios de cada valor individual com os valores críticos na tabela de critérios de Chauvenet abaixo. Para valores de dados individuais com desvios maiores que os encontrados na tabela, relate esses valores de dados como valores discrepantes.

O critério Chauvenet: um exemplo

Suponha que temos o seguinte conjunto de dados de 15 valores:

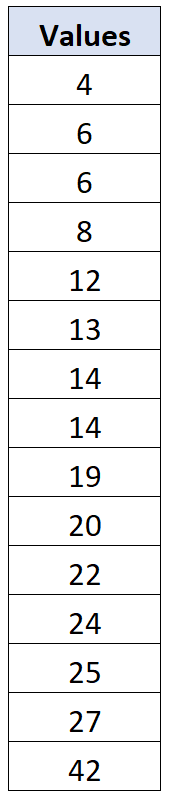
A média amostral para este conjunto de dados é x = 17,067 e o desvio padrão amostral é s = 10,096 . Para cada valor de dados individual, podemos calcular seu desvio da seguinte forma:

Desvio = |x _i – x | /s

Por exemplo:

• O primeiro valor dos dados teria um desvio de |4 – 17,067| / 10.096 = 1.294 .
• O primeiro valor dos dados teria um desvio de |6 – 17,067| / 10,096 = 1,096 .

E assim por diante.

Podemos usar a mesma fórmula para calcular o desvio de cada valor de dados individual:

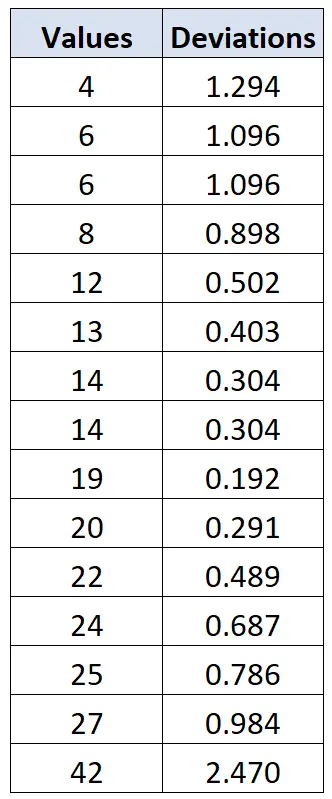
Podemos então consultar a tabela de critérios de Chauvenet e observar que o valor crítico que corresponde a um tamanho de amostra de n=15 é 2,128 . Assim, qualquer valor com desvio superior a 2,128 pode ser considerado um outlier.

Acontece que o valor 42 tem um desvio maior que 2,128:

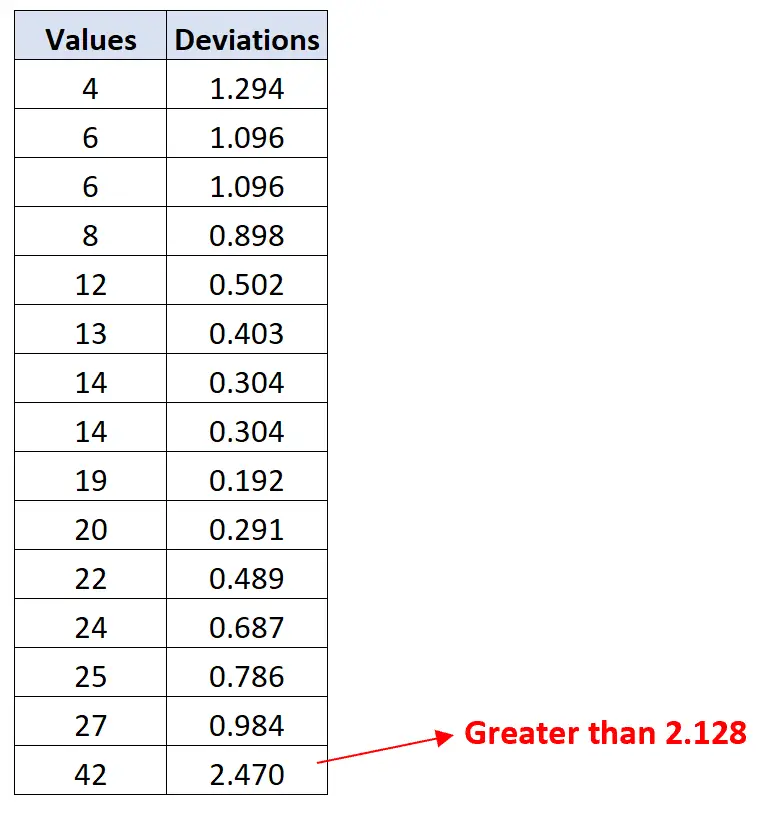
Assim, o valor 42 é o único outlier neste conjunto de dados.

Precauções quanto ao uso do critério de Chauvenet

O critério de Chauvenet assume que os valores em um conjunto de dados são normalmente distribuídos . Se esta suposição não for atendida, o uso do critério de Chauvenet para identificar valores discrepantes provavelmente não será válido.

Se você usar esse método e descobrir que um valor é atípico, primeiro verifique se o valor não é o resultado de um erro de entrada de dados. Às vezes, os dados são simplesmente inseridos incorretamente.

Se o valor for realmente atípico, você poderá optar por removê-lo se ele tiver um impacto significativo em sua análise geral. Apenas certifique-se de mencionar que você removeu um valor discrepante ao relatar seus resultados.

Além disso, este método só deve ser usado uma vez em um determinado conjunto de dados. Por exemplo, suponha que usamos este critério para identificar o valor 42 como um valor discrepante no exemplo anterior e remover esse valor do conjunto de dados.

Não devemos então recalcular a média amostral e o desvio padrão amostral e calcular os desvios novamente para encontrar mais valores discrepantes.