Como criar uma matriz de covariância no planilhas google

A covariância é uma medida de como as mudanças em uma variável estão associadas às mudanças em uma segunda variável. Mais especificamente, é uma medida do grau em que duas variáveis estão linearmente associadas.

A fórmula para calcular a covariância entre duas variáveis, X e Y é:

COV( X , Y ) = Σ(x- x )(y- y ) / n

Uma matriz de covariância é uma matriz quadrada que mostra a covariância entre muitas variáveis diferentes. Esta pode ser uma forma útil de compreender como diferentes variáveis estão relacionadas em um conjunto de dados.

O exemplo a seguir mostra como criar uma matriz de covariância no Planilhas Google para um determinado conjunto de dados.

Como criar uma matriz de covariância no Planilhas Google

Digamos que temos o seguinte conjunto de dados que mostra as pontuações dos testes de 10 alunos diferentes em três disciplinas: matemática, ciências e história.

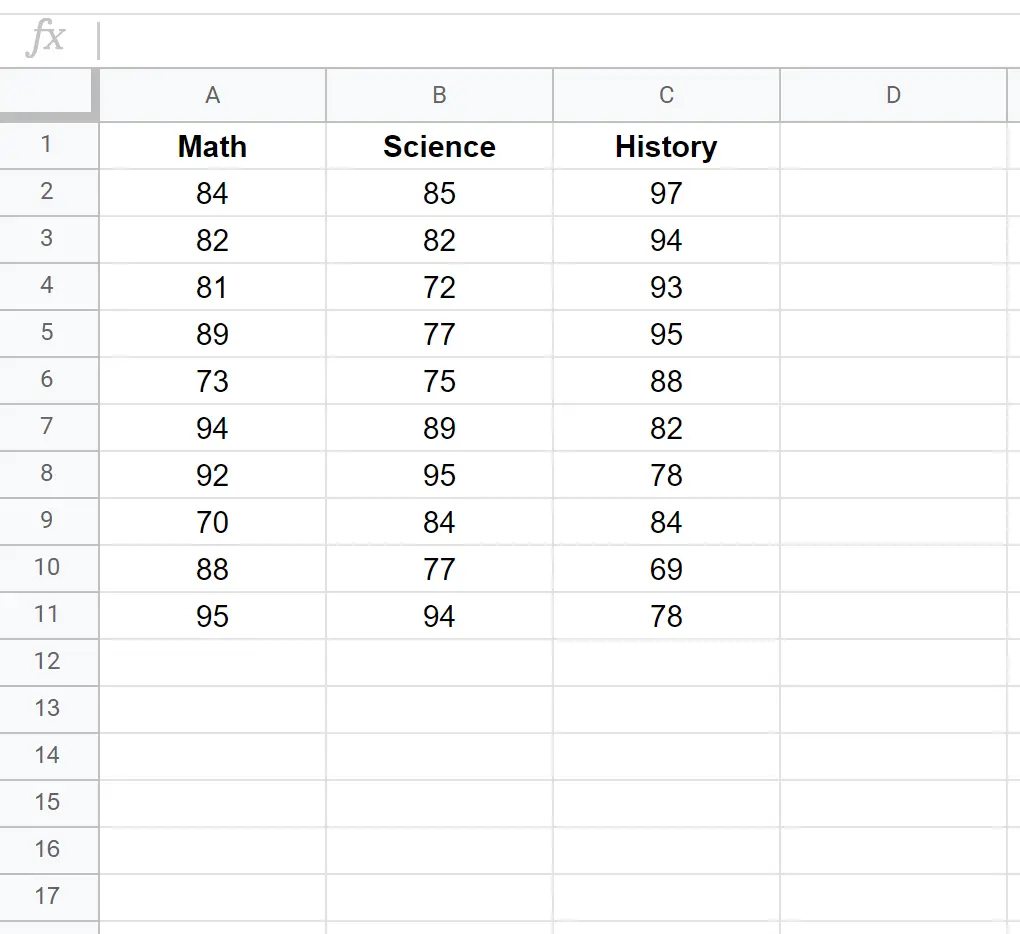
Para criar uma matriz de covariância para este conjunto de dados, podemos usar a função COVAR() com a seguinte sintaxe:

COVAR(dados_y, dados_x)

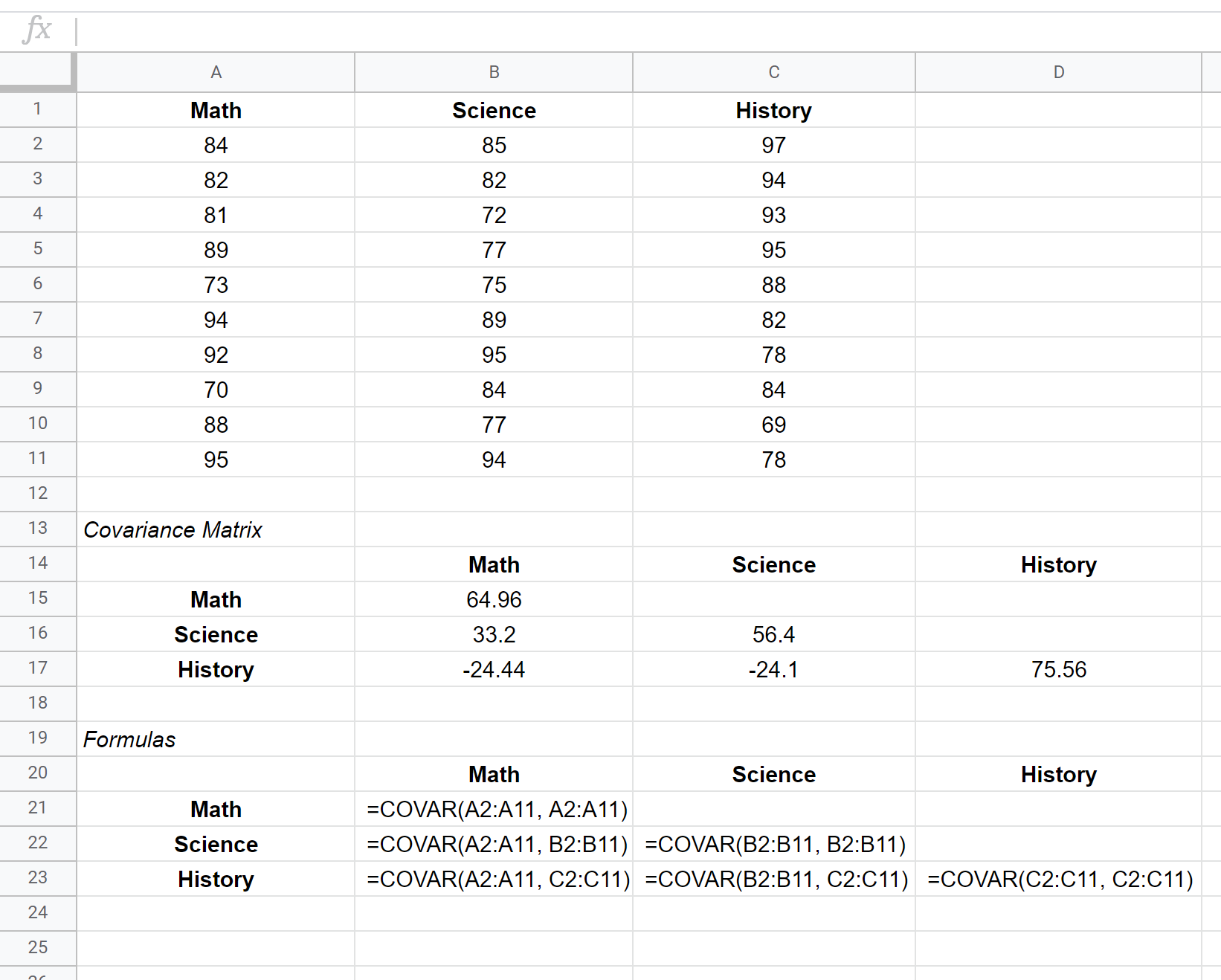
A matriz de covariância para este conjunto de dados é mostrada nas células B15:D17 , enquanto as fórmulas usadas para criar a matriz de covariância são mostradas nas células B21:D23 abaixo:

Como interpretar uma matriz de covariância

Assim que tivermos uma matriz de covariância, é simples interpretar os valores da matriz.

Os valores ao longo das diagonais da matriz são simplesmente as variâncias de cada assunto. Por exemplo:

• A variação das pontuações em matemática é 64,96
• A variação das pontuações em ciências é 56,4
• A variação histórica da pontuação é 75,56

Os demais valores da matriz representam as covariâncias entre os diferentes assuntos. Por exemplo:

• A covariância entre as pontuações em matemática e ciências é 33,2.
• A covariância entre as pontuações em matemática e história é -24,44.
• A covariância entre as pontuações de ciência e história é -24,1.

Um número positivo para covariância indica que duas variáveis tendem a aumentar ou diminuir em conjunto. Por exemplo, matemática e ciências têm uma covariância positiva (33,2), indicando que os alunos com notas altas em matemática também tendem a ter notas altas em ciências. Da mesma forma, os alunos com mau desempenho em matemática também tendem a ter mau desempenho em ciências.

Um número negativo para covariância indica que à medida que uma variável aumenta, uma segunda variável tende a diminuir. Por exemplo, matemática e história têm uma covariância negativa (-24,44), indicando que os alunos com notas altas em matemática tendem a ter notas baixas em história. Da mesma forma, os alunos com notas baixas em matemática tendem a ter notas altas em história.

Recursos adicionais

Como criar uma matriz de covariância no Excel
Como criar uma matriz de covariância em R
Como criar uma matriz de covariância em Python
Como criar uma matriz de covariância no SPSS