Como criar uma matriz de correlação no planilhas google

Uma forma de quantificar a relação entre duas variáveis é utilizar o coeficiente de correlação de Pearson , que é uma medida da associação linear entre duas variáveis . Tem um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Quanto mais longe o coeficiente de correlação estiver de zero, mais forte será a relação entre as duas variáveis.

Mas, em alguns casos, queremos compreender a correlação entre múltiplos pares de variáveis. Nestes casos, podemos criar uma matriz de correlação , que é uma tabela quadrada que mostra os coeficientes de correlação entre várias combinações de variáveis aos pares.

Este tutorial explica como criar e interpretar uma matriz de correlação no Planilhas Google.

Como criar uma matriz de correlação no Planilhas Google

Digamos que temos o seguinte conjunto de dados que mostra o número médio de pontos, rebotes e assistências de 10 jogadores de basquete:

Para criar uma matriz de correlação para este conjunto de dados, podemos usar a função CORREL() com a seguinte sintaxe:

  COVAR(dados_y, dados_x)

A matriz de covariância para este conjunto de dados é mostrada nas células B15:D17 , enquanto as fórmulas usadas para criar a matriz de covariância são mostradas nas células B21:D23 abaixo:

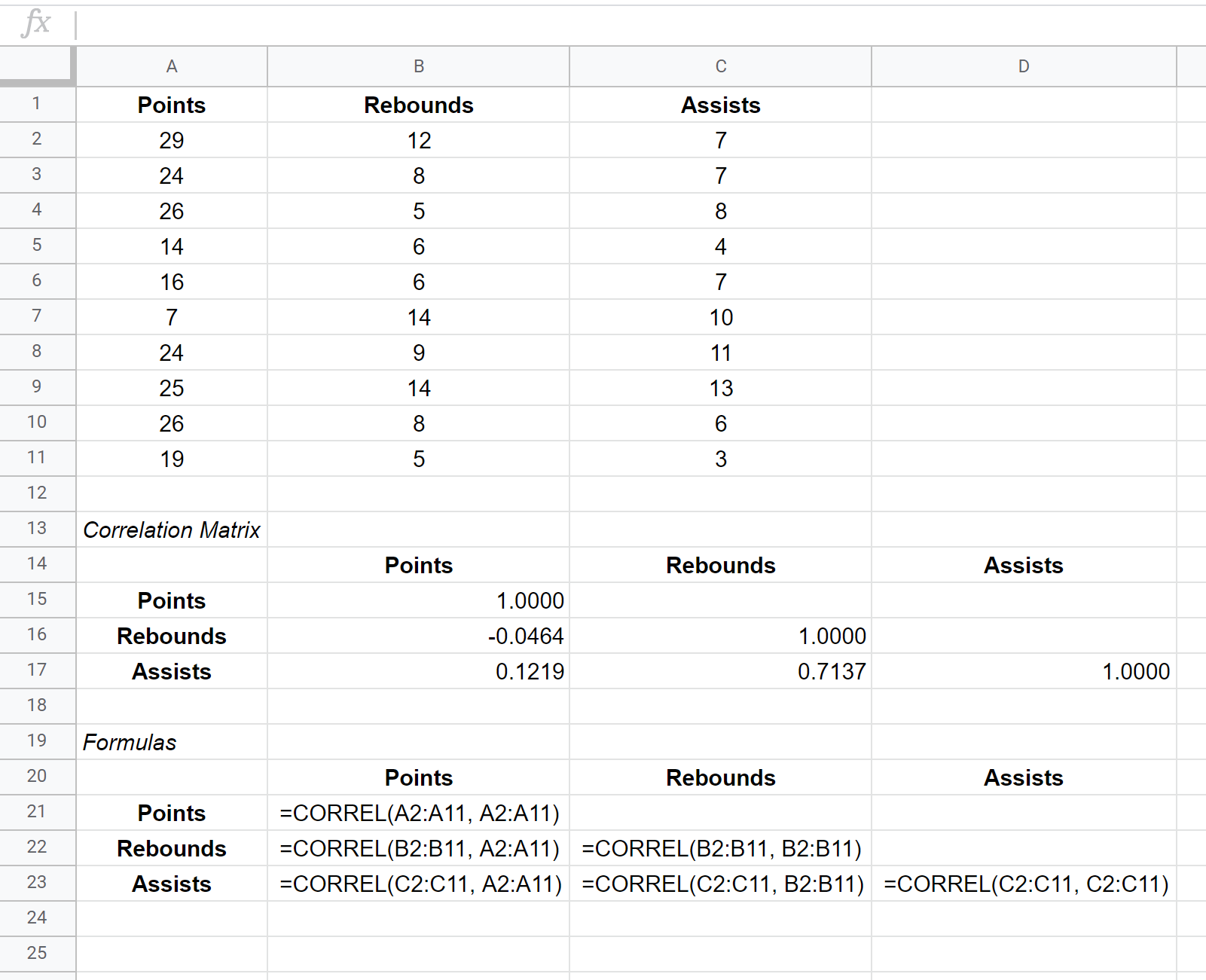
Como interpretar uma matriz de correlação

Os valores nas células individuais da matriz de correlação nos informam o coeficiente de correlação de Pearson entre cada combinação de variáveis aos pares. Por exemplo:

Correlação entre pontos e rebotes: -0,0464. Os pontos e os rebotes estão ligeiramente correlacionados negativamente, mas esse valor é tão próximo de zero que não há fortes evidências de uma associação significativa entre essas duas variáveis.

Correlação entre pontos e assistências: 0,1219. Os pontos e assistências estão ligeiramente correlacionados positivamente, mas este valor também é bastante próximo de zero, pelo que não há fortes evidências de uma associação significativa entre estas duas variáveis.

Correlação entre rebotes e assistências: 0,7137. Rebotes e assistências estão fortemente correlacionados positivamente. Ou seja, jogadores que têm mais rebotes também tendem a dar mais assistências.

Observe que os valores diagonais da matriz de correlação são todos 1 porque a correlação entre uma variável e ela mesma é sempre 1. Na prática, esse número não é útil para interpretação.

Recursos adicionais

Como ler uma matriz de correlação
Como criar uma matriz de correlação no Excel