Como calcular pontuações z no planilhas google

Nas estatísticas, uma pontuação z nos diz quantos desvios padrão um valor está da média . Usamos a seguinte fórmula para calcular uma pontuação z:

z = (X – μ) / σ

Ouro:

• X é um único valor de dados brutos
• μ é a média do conjunto de dados
• σ é o desvio padrão do conjunto de dados

Este tutorial explica como calcular pontuações z para valores de dados brutos no Planilhas Google.

Exemplo: pontuações z no Planilhas Google

Suponha que temos o seguinte conjunto de dados e desejamos encontrar a pontuação z para cada valor de dados brutos:

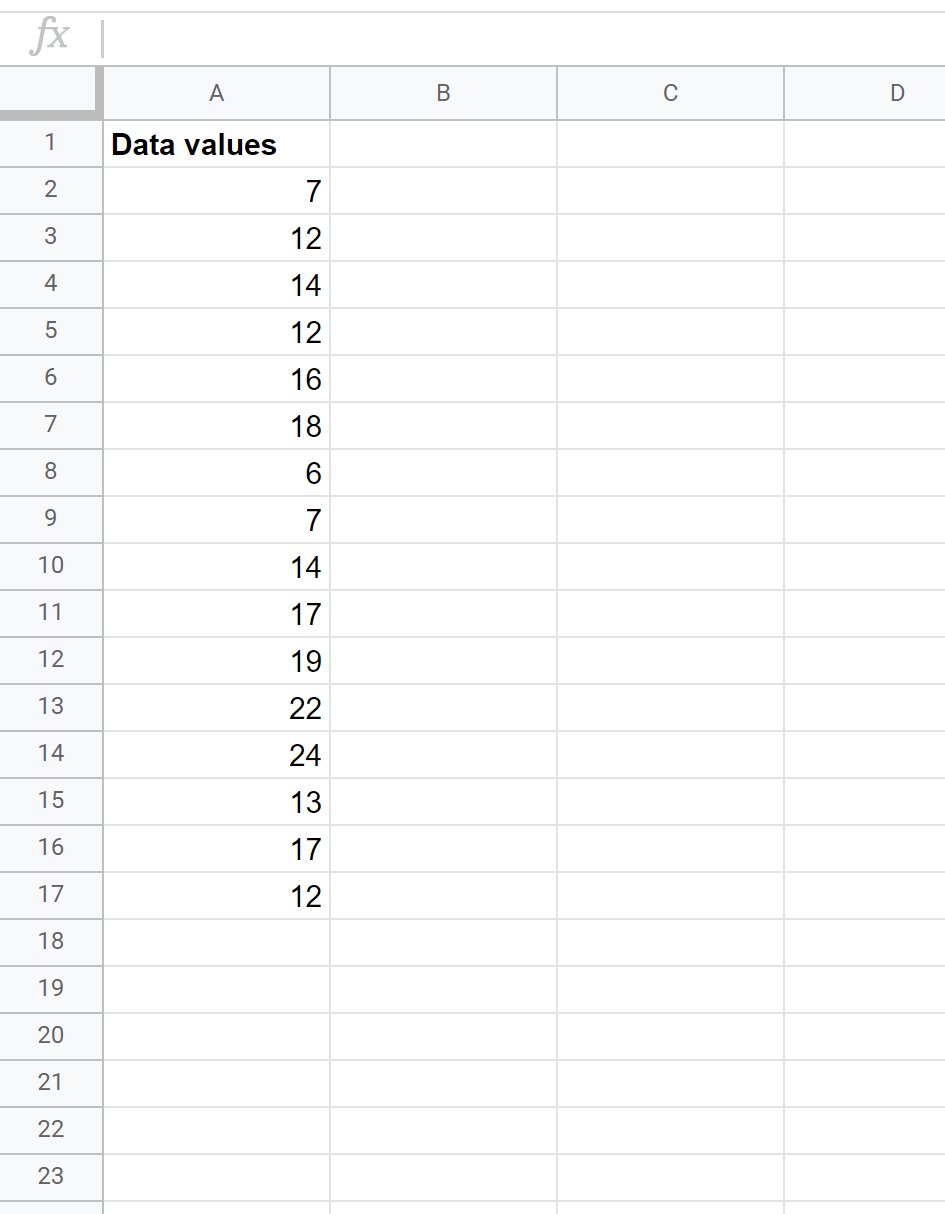
Podemos executar as seguintes etapas para fazer isso.

Etapa 1: Encontre a média e o desvio padrão do conjunto de dados.

Primeiro, precisamos encontrar a média e o desvio padrão do conjunto de dados. As fórmulas a seguir mostram como fazer isso:

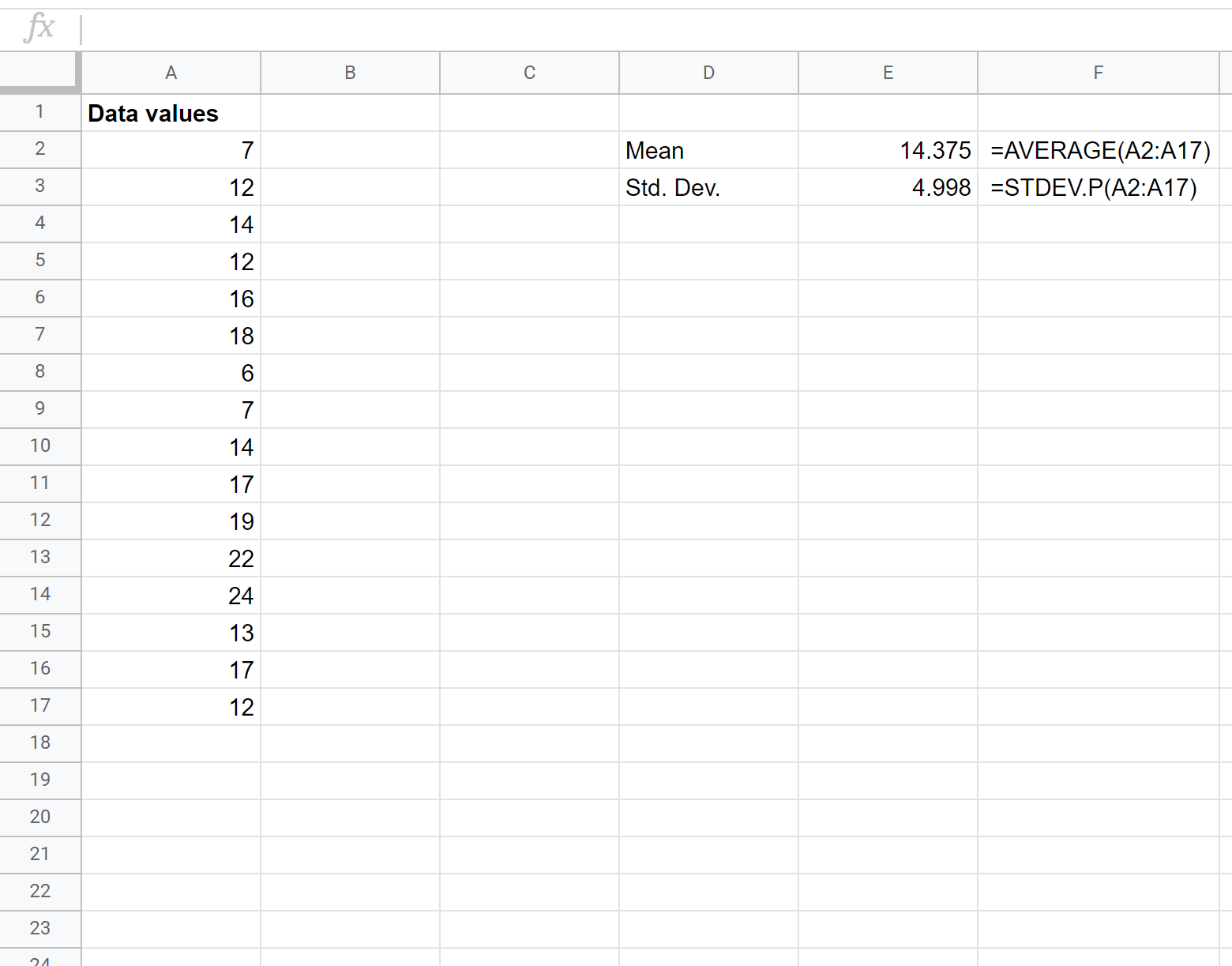
A média é 14,375 e o desvio padrão é 4,998 .

Etapa 2: Encontre a pontuação z para o primeiro valor de dados brutos.

A seguir, encontraremos a pontuação z para o primeiro valor de dados brutos digitando a seguinte fórmula na célula B2:

= ( A2 – $E$2 ) / $E$3

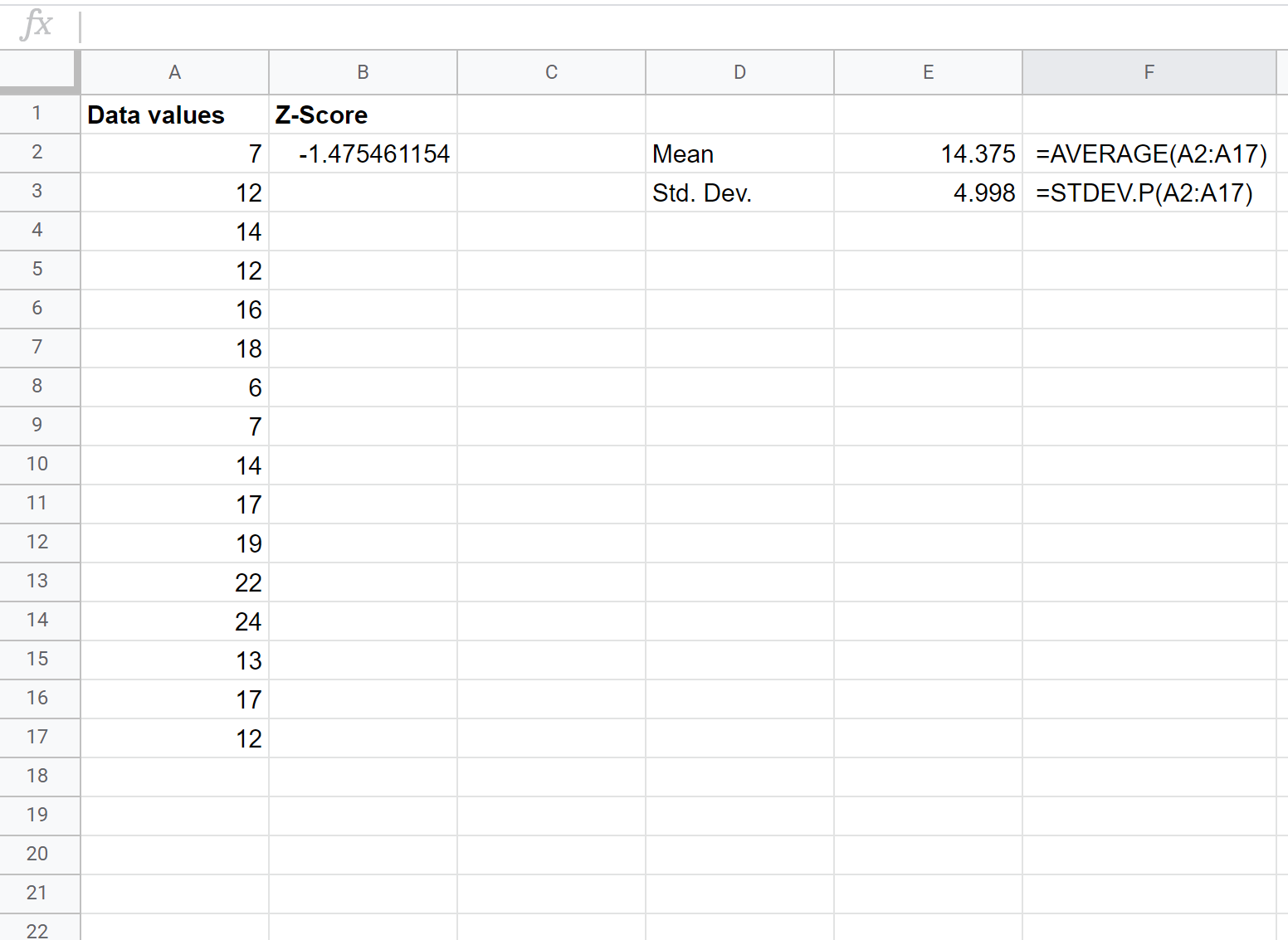
Etapa 3: Encontre as pontuações z para todos os valores restantes.

Depois de calcularmos o primeiro escore z, podemos destacar o restante da coluna B começando pela célula B2 e pressionar Ctrl+D para copiar a fórmula da célula B2 para cada uma das células abaixo:

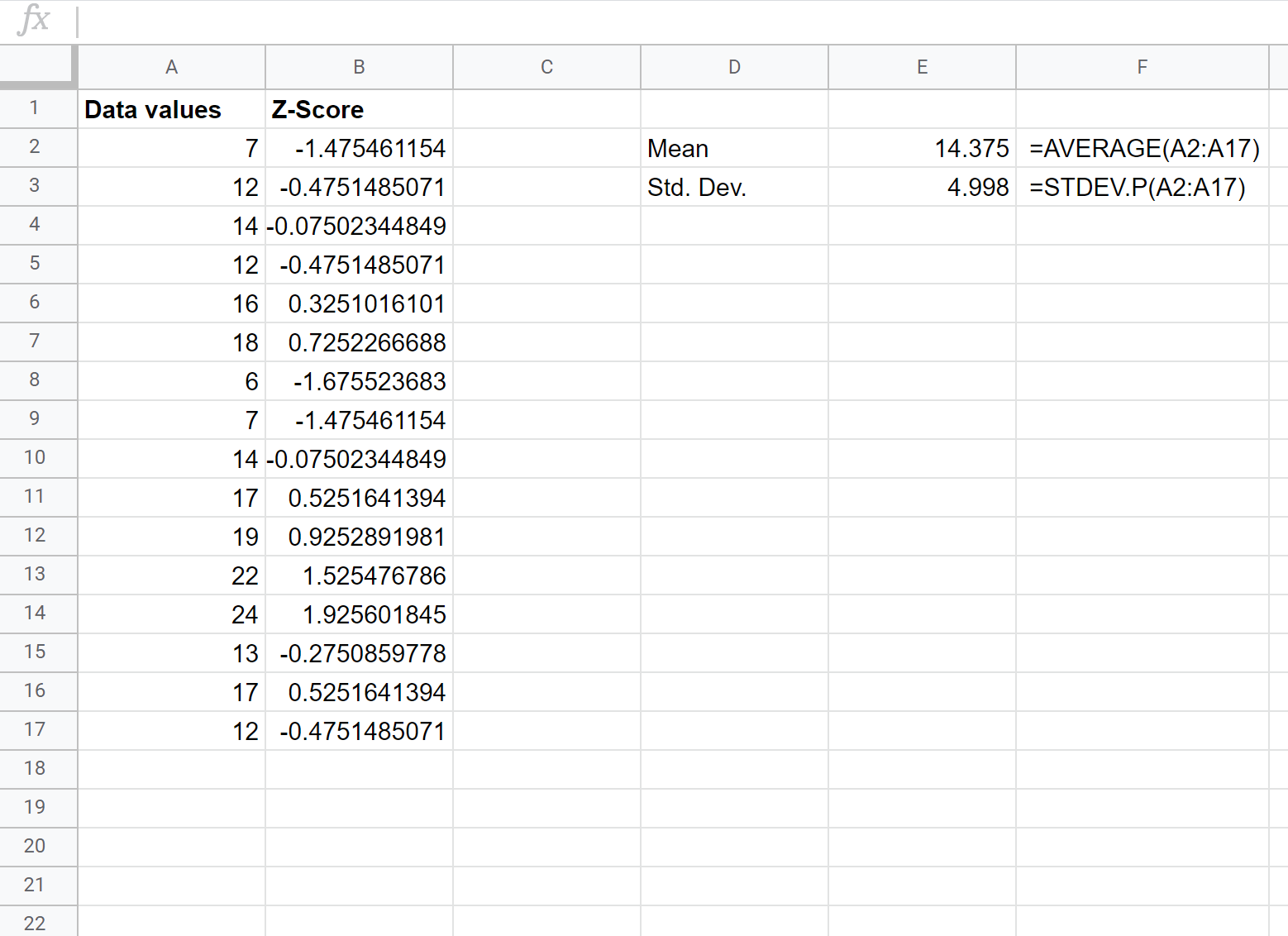
Agora encontramos a pontuação z para cada valor de dados brutos.

Como interpretar pontuações Z

Uma pontuação z simplesmente nos diz quantos desvios padrão um valor está da média.

No nosso exemplo, descobrimos que a média era 14,375 e o desvio padrão era 4,998 .

Portanto, o primeiro valor em nosso conjunto de dados foi 7, que teve uma pontuação z de (7-14,375) / 4,998 = -1,47546 . Isso significa que o valor “7” é -1,47545 desvios padrão inferior à média.

O próximo valor em nossos dados, 12, teve uma pontuação z de (12-14,375) / 4,998 = -0,47515 . Isto significa que o valor “12” é -0,47515 desvios padrão inferior à média.

Quanto mais distante um valor estiver da média, maior será o valor absoluto do escore z para esse valor. Por exemplo, o valor 7 está mais distante da média (14,375) do que o valor 12, o que explica porque 7 teve um escore z com valor absoluto maior.

Recursos adicionais

Como calcular pontuações Z no Excel
Como calcular pontuações Z em R
Como calcular pontuações Z em uma calculadora TI-84