Como calcular assimetria e curtose em r
Nas estatísticas, a assimetria e a curtose são duas maneiras de medir a forma de uma distribuição.
A assimetria é uma medida da assimetria de uma distribuição. Este valor pode ser positivo ou negativo.
- A assimetria negativa indica que a cauda está no lado esquerdo da distribuição, que se estende em direção a valores mais negativos.
- Uma inclinação positiva indica que a cauda está no lado direito da distribuição, que se estende em direção a valores mais positivos.
- Um valor zero indica que não há assimetria na distribuição, o que significa que a distribuição é perfeitamente simétrica.
A curtose é uma medida para saber se uma distribuição tem cauda pesada ou leve em comparação com uma distribuição normal .
- A curtose de uma distribuição normal é 3.
- Se uma determinada distribuição tiver uma curtose menor que 3, ela é considerada playkurtica , o que significa que tende a produzir menos valores discrepantes e menos extremos do que a distribuição normal.
- Se uma determinada distribuição tiver curtose superior a 3, diz-se que é leptocúrtica , o que significa que tende a produzir mais valores discrepantes do que a distribuição normal.
Nota: Algumas fórmulas (definição de Fisher) subtraem 3 da curtose para facilitar a comparação com a distribuição normal. Usando esta definição, uma distribuição teria maior curtose do que uma distribuição normal se tivesse um valor de curtose maior que 0.
Este tutorial explica como calcular a assimetria e a curtose de um determinado conjunto de dados em R.
Exemplo: assimetria e achatamento em R
Suponha que temos o seguinte conjunto de dados:
data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)
Podemos visualizar rapidamente a distribuição dos valores neste conjunto de dados criando um histograma:
hist(data, col=' steelblue ')
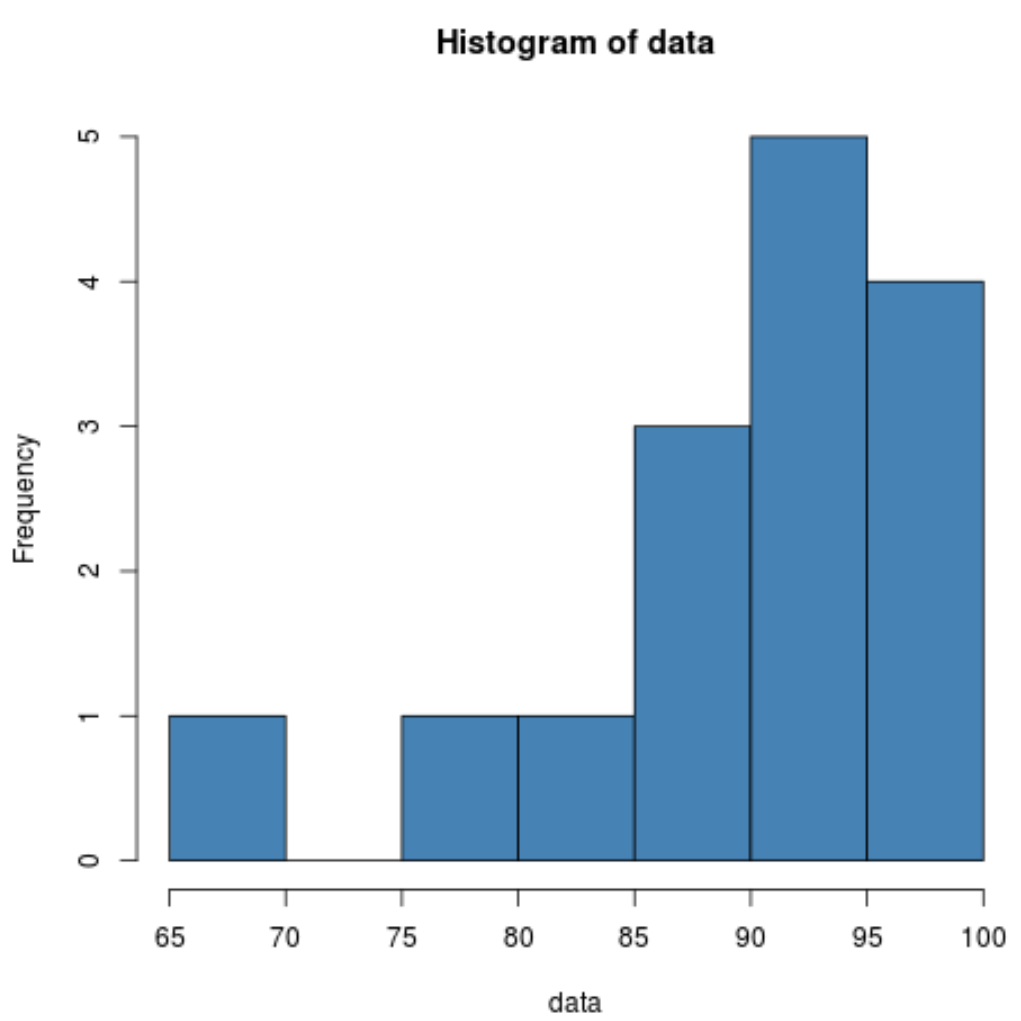
O histograma mostra-nos que a distribuição parece estar distorcida para a esquerda. Ou seja, uma parcela maior dos valores está concentrada no lado direito da distribuição.
Para calcular a assimetria e a curtose deste conjunto de dados, podemos usar as funções skewness() e kurtosis() da biblioteca de momentos em R:
library (moments) #calculate skewness skewness(data) [1] -1.391777 #calculate kurtosis kurtosis(data) [1] 4.177865
A assimetria é -1,391777 e a curtose é 4,177865 .
Como a assimetria é negativa, isso indica que a distribuição permanece distorcida. Isso confirma o que vimos no histograma.
Como a curtose é maior que 3, isso indica que a distribuição tem mais valores nas caudas em comparação com uma distribuição normal.
A biblioteca de momentos também oferece a função jarque.test() , que executa um teste de adequação que determina se os dados da amostra apresentam assimetria e curtose consistentes com uma distribuição normal. As hipóteses nula e alternativa deste teste são as seguintes:
Hipótese nula : o conjunto de dados apresenta assimetria e curtose que correspondem a uma distribuição normal.
Hipótese alternativa : o conjunto de dados apresenta distorção e curtose que não corresponde a uma distribuição normal.
O código a seguir mostra como realizar esse teste:
jarque.test(data)
Jarque-Bera Normality Test
data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater
O valor p do teste é 0,05756 . Como este valor não é inferior a α = 0,05, não rejeitamos a hipótese nula. Não temos evidências suficientes para dizer que este conjunto de dados apresenta assimetria e curtose diferentes da distribuição normal.
Você pode encontrar a documentação completa da Biblioteca Moments aqui .
Bônus: calculadora de assimetria e curtose
Você também pode calcular a assimetria de um determinado conjunto de dados usando a Calculadora estatística de assimetria e curtose , que calcula automaticamente a assimetria e a curtose de um determinado conjunto de dados.