Introdução à regressão logística

Quando queremos entender a relação entre uma ou mais variáveis preditoras e uma variável de resposta contínua, geralmente usamos a regressão linear .

Porém, quando a variável resposta é categórica, podemos utilizar a regressão logística .

A regressão logística é um tipo de algoritmo de classificação porque tenta “classificar” as observações em um conjunto de dados em categorias distintas.

Aqui estão alguns exemplos de uso de regressão logística:

• Queremos usar a pontuação de crédito e o saldo bancário para prever se um determinado cliente deixará de pagar um empréstimo. (Variável de resposta = “Padrão” ou “Sem padrão”)
• Queremos usar a média de rebotes por jogo e a média de pontos por jogo para prever se um determinado jogador de basquete será ou não convocado para a NBA (variável de resposta = “Drafted” ou “Undrafted”).
• Queremos usar a metragem quadrada e o número de banheiros para prever se uma casa em uma determinada cidade será ou não listada a um preço de venda de US$ 200.000 ou mais. (Variável de resposta = “Sim” ou “Não”)

Observe que a variável de resposta em cada um desses exemplos só pode assumir um de dois valores. Compare isso com a regressão linear na qual a variável de resposta assume um valor contínuo.

A equação de regressão logística

A regressão logística usa um método conhecido como estimativa de máxima verossimilhança (os detalhes não serão discutidos aqui) para encontrar uma equação da seguinte forma:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ +… + β _p

Ouro:

• X _j : a j- ^ésima variável preditiva
• β _j : estimativa do coeficiente para a j ^-ésima variável preditiva

A fórmula no lado direito da equação prevê o log de probabilidade de que a variável de resposta assuma o valor 1.

Assim, quando ajustamos um modelo de regressão logística, podemos usar a seguinte equação para calcular a probabilidade de uma determinada observação assumir o valor 1:

p(X) = e ^{β ₀ + β _{1 X 1 + β 2 X 2 + … + β p}}

Em seguida, usamos um certo limite de probabilidade para classificar a observação como 1 ou 0.

Por exemplo, poderíamos dizer que as observações com probabilidade maior ou igual a 0,5 serão classificadas como “1” e todas as outras observações serão classificadas como “0”.

Como interpretar o resultado da regressão logística

Suponha que usemos um modelo de regressão logística para prever se um determinado jogador de basquete será ou não convocado para a NBA com base na média de rebotes por jogo e na média de pontos por jogo.

Aqui está o resultado do modelo de regressão logística:

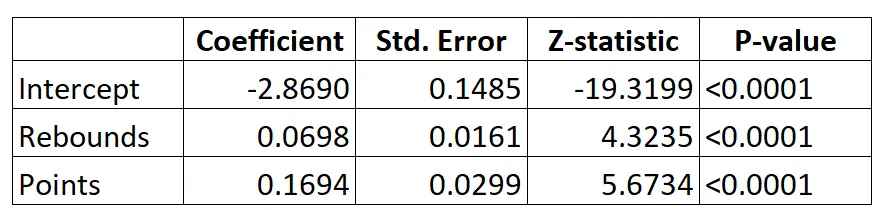
Usando os coeficientes, podemos calcular a probabilidade de um determinado jogador ser convocado para a NBA com base na média de rebotes e pontos por jogo usando a seguinte fórmula:

P(Elaborado) = e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(pontos)} / (1+e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(pontos) ) )}

Por exemplo, digamos que um determinado jogador tenha em média 8 rebotes por jogo e 15 pontos por jogo. De acordo com o modelo, a probabilidade deste jogador ser convocado para a NBA é de 0,557 .

P(Escrito) = e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} / (1+e ^{-2,8690 + 0,0698*(8) + 0,1694*(15 )} ) = 0,557

Como esta probabilidade é superior a 0,5, prevemos que este jogador será convocado.

Compare isso com um jogador que tem média de apenas 3 rebotes e 7 pontos por jogo. A probabilidade deste jogador ser convocado para a NBA é de 0,186 .

P(Escrito) = e ^{-2,8690 + 0,0698*(3) + 0,1694*(7)} / (1+e ^{-2,8690 + 0,0698*(3) + 0,1694*(7 )} ) = 0,186

Como esta probabilidade é inferior a 0,5, prevemos que este jogador não será convocado.

Suposições de regressão logística

A regressão logística usa as seguintes suposições:

1. A variável de resposta é binária. Supõe-se que a variável resposta só pode assumir dois resultados possíveis.

2. As observações são independentes. Supõe-se que as observações no conjunto de dados são independentes umas das outras. Ou seja, as observações não devem provir de medições repetidas do mesmo indivíduo ou estar relacionadas entre si de alguma forma.

3. Não há multicolinearidade séria entre as variáveis preditoras . Supõe-se que nenhuma das variáveis preditoras esteja altamente correlacionada entre si.

4. Não existem valores discrepantes extremos. Supõe-se que não haja valores discrepantes extremos ou observações influentes no conjunto de dados.

5. Existe uma relação linear entre as variáveis preditoras e o logit da variável resposta . Esta hipótese pode ser testada usando um teste de Box-Tidwell.

6. O tamanho da amostra é grande o suficiente. Normalmente, você deve ter no mínimo 10 casos com o resultado menos frequente para cada variável explicativa. Por exemplo, se você tiver 3 variáveis explicativas e a probabilidade esperada do resultado menos frequente for 0,20, então você deverá ter um tamanho de amostra de pelo menos (10*3) / 0,20 = 150.

Confira este artigo para obter uma explicação detalhada de como verificar essas suposições.