Como realizar regressão logística em python (passo a passo)

A regressão logística é um método que podemos usar para ajustar um modelo de regressão quando a variável de resposta é binária.

A regressão logística usa um método conhecido como estimativa de máxima verossimilhança para encontrar uma equação da seguinte forma:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ +… + β _p

Ouro:

• X _j : a j- ^ésima variável preditiva
• β _j : estimativa do coeficiente para a j ^-ésima variável preditiva

A fórmula no lado direito da equação prevê o log de probabilidade de que a variável de resposta assuma o valor 1.

Assim, quando ajustamos um modelo de regressão logística, podemos usar a seguinte equação para calcular a probabilidade de uma determinada observação assumir o valor 1:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Em seguida, usamos um certo limite de probabilidade para classificar a observação como 1 ou 0.

Por exemplo, poderíamos dizer que as observações com probabilidade maior ou igual a 0,5 serão classificadas como “1” e todas as outras observações serão classificadas como “0”.

Este tutorial fornece um exemplo passo a passo de como realizar regressão logística em R.

Passo 1: Importe os pacotes necessários

Primeiramente, importaremos os pacotes necessários para realizar a regressão logística em Python:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Etapa 2: carregar dados

Para este exemplo, usaremos o conjunto de dados padrão do livro Introdução ao Aprendizado Estatístico . Podemos usar o seguinte código para carregar e exibir um resumo do conjunto de dados:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

Este conjunto de dados contém as seguintes informações sobre 10.000 indivíduos:

• inadimplência: indica se um indivíduo está inadimplente ou não.
• estudante: indica se um indivíduo é estudante ou não.
• saldo: Saldo médio mantido por um indivíduo.
• renda: Renda da pessoa física.

Usaremos a situação estudantil, o saldo bancário e a renda para construir um modelo de regressão logística que prevê a probabilidade de inadimplência de um determinado indivíduo.

Etapa 3: criar amostras de treinamento e teste

A seguir, dividiremos o conjunto de dados em um conjunto de treinamento para treinar o modelo e um conjunto de teste para testar o modelo.

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

Passo 4: Ajustar o modelo de regressão logística

A seguir, usaremos a função LogisticRegression() para ajustar um modelo de regressão logística ao conjunto de dados:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

Etapa 5: diagnóstico do modelo

Depois de ajustar o modelo de regressão, podemos analisar o desempenho do nosso modelo no conjunto de dados de teste.

Primeiro, criaremos a matriz de confusão para o modelo:

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

Da matriz de confusão podemos ver que:

• #Verdadeiras previsões positivas: 2.886
• #Previsões negativas verdadeiras: 0
• #Previsões falsas positivas: 113
• #Previsões falsas negativas: 1

Também podemos obter o modelo de precisão, que nos informa a porcentagem de previsões de correção feitas pelo modelo:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

Isso nos diz que o modelo fez a previsão correta sobre se um indivíduo entraria em default ou não em 96,2% das vezes.

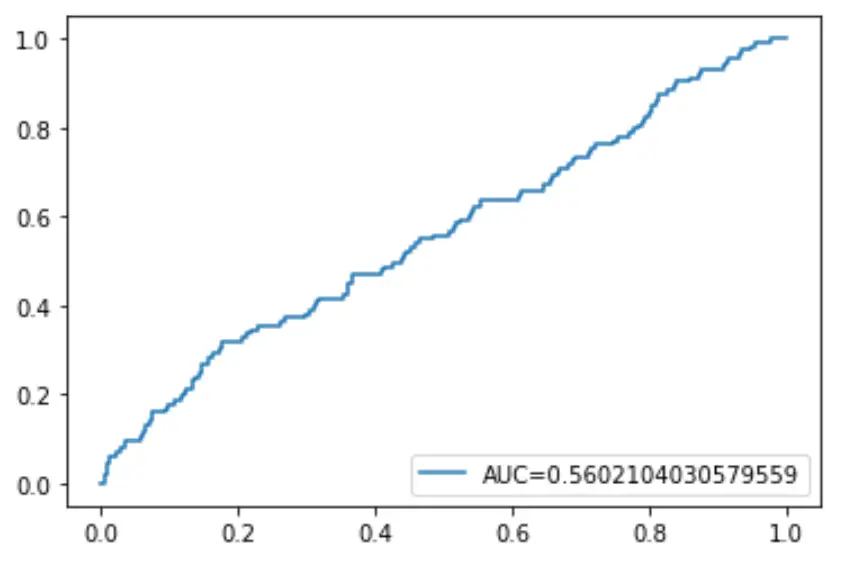
Finalmente, podemos traçar a curva Receiver Operating Characteristic (ROC), que exibe a porcentagem de verdadeiros positivos previstos pelo modelo quando o limite de probabilidade de predição é reduzido de 1 para 0.

Quanto maior a AUC (área sob a curva), mais precisamente o nosso modelo é capaz de prever os resultados:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()