Análise discriminante linear em r (passo a passo)

A análise discriminante linear é um método que você pode usar quando possui um conjunto de variáveis preditoras e deseja classificar uma variável de resposta em duas ou mais classes.

Este tutorial fornece um exemplo passo a passo de como realizar análise discriminante linear em R.

Etapa 1: carregue as bibliotecas necessárias

Primeiro, carregaremos as bibliotecas necessárias para este exemplo:

 library (MASS)
library (ggplot2)

Etapa 2: carregar dados

Para este exemplo, usaremos o conjunto de dados iris integrado em R. O código a seguir mostra como carregar e exibir este conjunto de dados:

 #attach iris dataset to make it easy to work with
attach(iris)

#view structure of dataset
str(iris)

'data.frame': 150 obs. of 5 variables:
 $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...

Podemos ver que o conjunto de dados contém 5 variáveis e 150 observações no total.

Para este exemplo, construiremos um modelo de análise discriminante linear para classificar a qual espécie pertence uma determinada flor.

Usaremos as seguintes variáveis preditoras no modelo:

• Sépala.comprimento
• Sépala.Largura
• Pétala.Comprimento
• Pétala.Largura

E vamos usá-los para prever a variável de resposta Species , que suporta as três classes potenciais a seguir:

• setosa
• versicolor
• Virgínia

Etapa 3: dimensionar os dados

Uma das principais suposições da análise discriminante linear é que cada uma das variáveis preditoras tem a mesma variância. Uma maneira simples de garantir que essa suposição seja atendida é dimensionar cada variável de modo que ela tenha média 0 e desvio padrão 1.

Podemos fazer isso rapidamente em R usando a função scale() :

 #scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])

Podemos usar a função apply() para verificar se cada variável preditora agora tem uma média de 0 e um desvio padrão de 1:

 #find mean of each predictor variable
apply(iris[1:4], 2, mean)

 Sepal.Length Sepal.Width Petal.Length Petal.Width 
-4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 

#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd) 

Sepal.Length Sepal.Width Petal.Length Petal.Width 
           1 1 1 1

Etapa 4: criar amostras de treinamento e teste

A seguir, dividiremos o conjunto de dados em um conjunto de treinamento para treinar o modelo e um conjunto de teste para testar o modelo:

 #make this example reproducible
set.seed(1)

#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ] 

Etapa 5: ajuste o modelo LDA

A seguir, usaremos a função lda() do pacote MASS para adaptar o modelo LDA aos nossos dados:

 #fit LDA model
model <- lda(Species~., data=train)

#view model output
model

Call:
lda(Species ~ ., data = train)

Prior probabilities of groups:
    setosa versicolor virginica 
 0.3207547 0.3207547 0.3584906 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa -1.0397484 0.8131654 -1.2891006 -1.2570316
versicolor 0.1820921 -0.6038909 0.3403524 0.2208153
virginica 0.9582674 -0.1919146 1.0389776 1.1229172

Coefficients of linear discriminants:
                    LD1 LD2
Sepal.Length 0.7922820 0.5294210
Sepal.Width 0.5710586 0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width -2.0602181 2.6326229

Proportion of traces:
   LD1 LD2 
0.9921 0.0079 

Veja como interpretar os resultados do modelo:

Probabilidades anteriores do grupo: representam as proporções de cada espécie no conjunto de treinamento. Por exemplo, 35,8% de todas as observações no conjunto de treinamento foram para a espécie virginica .

Médias de grupo: exibem os valores médios de cada variável preditora para cada espécie.

Coeficientes discriminantes lineares: exibem a combinação linear de variáveis preditoras usadas para treinar a regra de decisão do modelo LDA. Por exemplo:

• LD1: 0,792 * comprimento da sépala + 0,571 * largura da sépala – 4,076 * comprimento da pétala – 2,06 * largura da pétala
• LD2: 0,529 * comprimento da sépala + 0,713 * largura da sépala – 2,731 * comprimento da pétala + 2,63 * largura da pétala

Proporção de rastreamento: exibem a porcentagem de separação alcançada por cada função discriminante linear.

Etapa 6: use o modelo para fazer previsões

Depois de ajustar o modelo usando nossos dados de treinamento, podemos usá-lo para fazer previsões sobre nossos dados de teste:

 #use LDA model to make predictions on test data
predicted <- predict (model, test)

names(predicted)

[1] "class" "posterior" "x"   

Isso retorna uma lista com três variáveis:

• classe: a classe prevista
• posterior: A probabilidade posterior de que uma observação pertença a cada classe
• x: Discriminantes lineares

Podemos visualizar rapidamente cada um desses resultados para as primeiras seis observações em nosso conjunto de dados de teste:

 #view predicted class for first six observations in test set
head(predicted$class)

[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica

#view posterior probabilities for first six observations in test set
head(predicted$posterior)

   setosa versicolor virginica
4 1 2.425563e-17 1.341984e-35
6 1 1.400976e-21 4.482684e-40
7 1 3.345770e-19 1.511748e-37
15 1 6.389105e-31 7.361660e-53
17 1 1.193282e-25 2.238696e-45
18 1 6.445594e-22 4.894053e-41

#view linear discriminants for first six observations in test set
head(predicted$x)

         LD1 LD2
4 7.150360 -0.7177382
6 7.961538 1.4839408
7 7.504033 0.2731178
15 10.170378 1.9859027
17 8.885168 2.1026494
18 8.113443 0.7563902

Podemos usar o código a seguir para ver qual porcentagem de observações o modelo LDA previu corretamente a espécie:

 #find accuracy of model
mean(predicted$class==test$Species)

[1] 1

Acontece que o modelo previu corretamente as espécies para 100% das observações em nosso conjunto de dados de teste.

No mundo real, um modelo LDA raramente prevê corretamente os resultados de cada classe, mas esse conjunto de dados da íris é simplesmente construído de uma forma que os algoritmos de aprendizado de máquina tendem a ter um desempenho muito bom.

Passo 7: Visualize os resultados

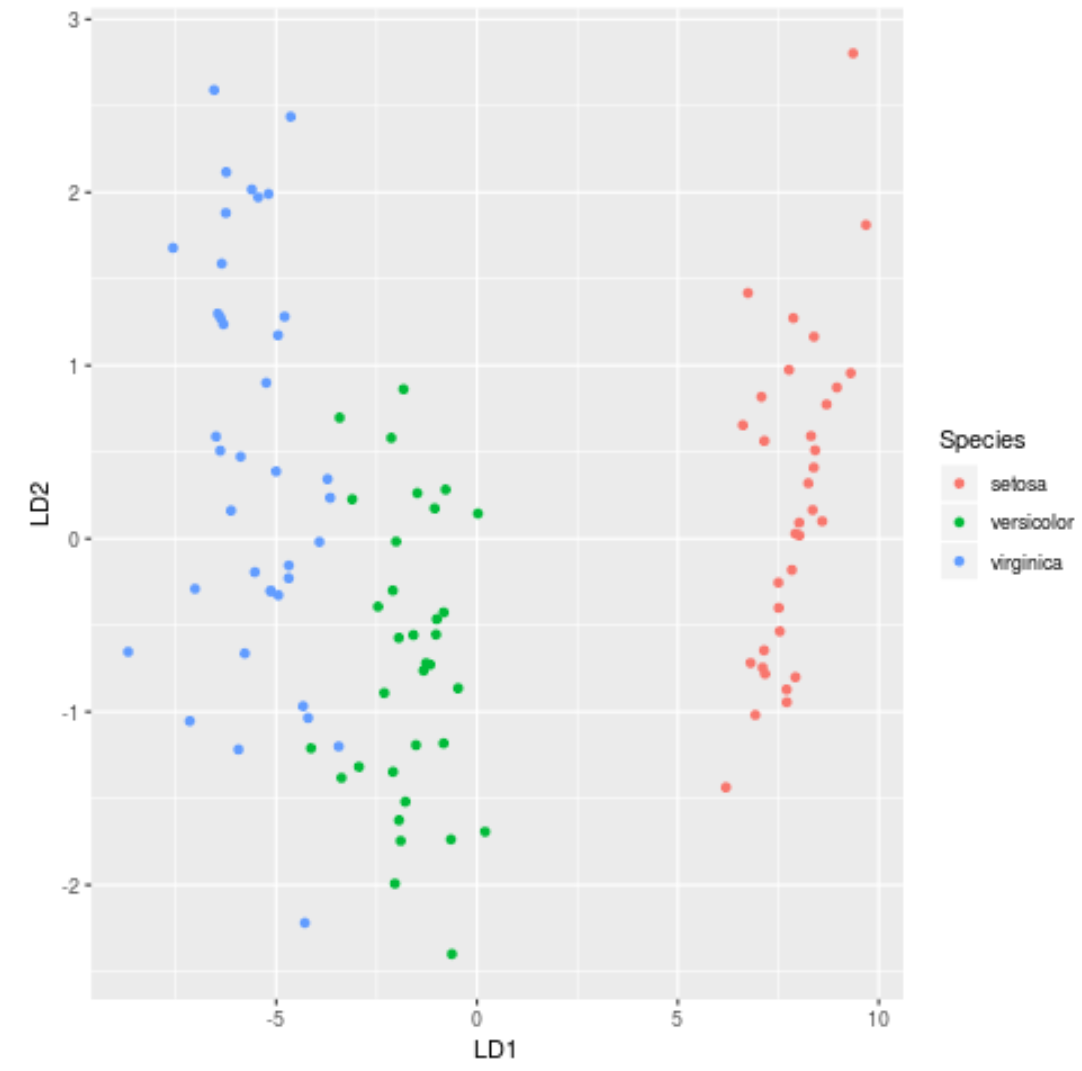
Finalmente, podemos criar um gráfico LDA para visualizar os discriminantes lineares do modelo e visualizar quão bem ele separa as três espécies diferentes em nosso conjunto de dados:

 #define data to plot
lda_plot <- cbind(train, predict(model)$x)

#createplot
ggplot(lda_plot, aes (LD1, LD2)) +
  geom_point( aes (color=Species))

Você pode encontrar o código R completo usado neste tutorial aqui .