O que é overfitting no aprendizado de máquina? (explicação e exemplos)
No aprendizado de máquina, muitas vezes construímos modelos para que possamos fazer previsões precisas sobre determinados fenômenos.
Por exemplo, suponha que queiramos criar um modelo de regressão que use a variável preditora horas gastas estudando para prever a pontuação ACT da variável de resposta para alunos do ensino médio.
Para construir este modelo, coletaremos dados sobre horas gastas estudando e a pontuação ACT correspondente para centenas de alunos em um determinado distrito escolar.
Usaremos então esses dados para treinar um modelo que possa fazer previsões sobre a pontuação que um determinado aluno receberá com base no número total de horas estudadas.
Para avaliar a utilidade do modelo, podemos medir até que ponto as previsões do modelo correspondem aos dados observados. Uma das métricas mais comumente usadas para fazer isso é o erro quadrático médio (MSE), que é calculado da seguinte forma:
MSE = (1/n)*Σ(y i – f(x i )) 2
Ouro:
- n: número total de observações
- y i : O valor da resposta da i-ésima observação
- f (x i ): O valor de resposta previsto da i- ésima observação
Quanto mais próximas as previsões do modelo estiverem das observações, menor será o MSE.
No entanto, um dos maiores erros cometidos no aprendizado de máquina é otimizar modelos para reduzir o MSE de treinamento , ou seja, quão bem as previsões do modelo correspondem aos dados que usamos para treinar o modelo.
Quando um modelo se concentra demais na redução do MSE de treinamento, muitas vezes é muito difícil encontrar padrões nos dados de treinamento que são simplesmente causados pelo acaso. Então, quando o modelo é aplicado a dados não vistos, seu desempenho é ruim.
Este fenômeno é conhecido como overfitting . Isso acontece quando “ajustamos” um modelo muito próximo aos dados de treinamento e, assim, acabamos construindo um modelo que não é útil para fazer previsões sobre novos dados.
Exemplo de sobreajuste
Para entender o overfitting, vamos voltar ao exemplo da criação de um modelo de regressão que usa horas gastas estudando para prever a pontuação do ACT .
Digamos que reunimos dados de 100 alunos em um determinado distrito escolar e criamos um gráfico de dispersão rápido para visualizar a relação entre as duas variáveis:
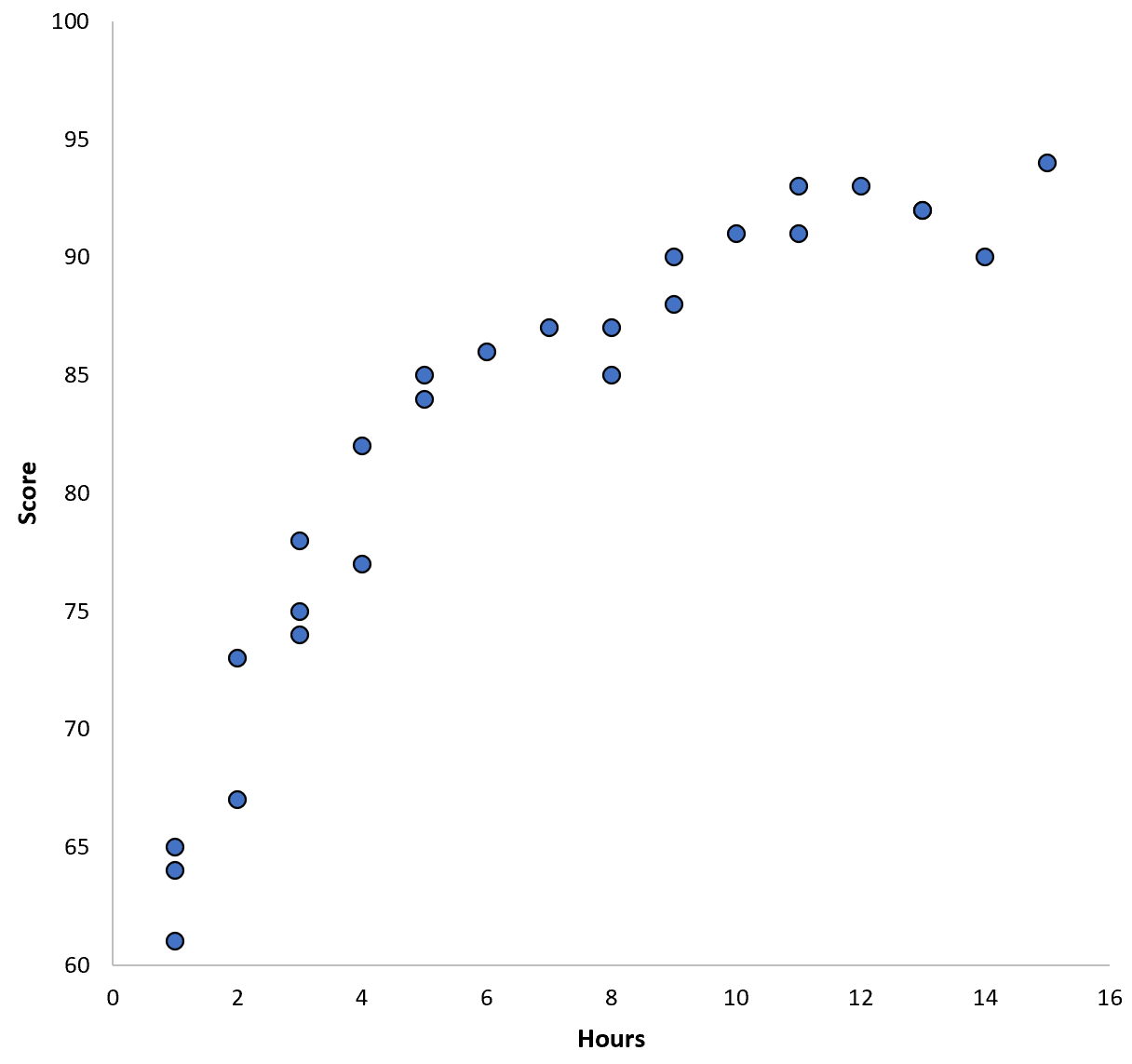
A relação entre as duas variáveis parece ser quadrática, então suponhamos que aplicamos o seguinte modelo de regressão quadrática:
Pontuação = 60,1 + 5,4*(Horas) – 0,2*(Horas) 2
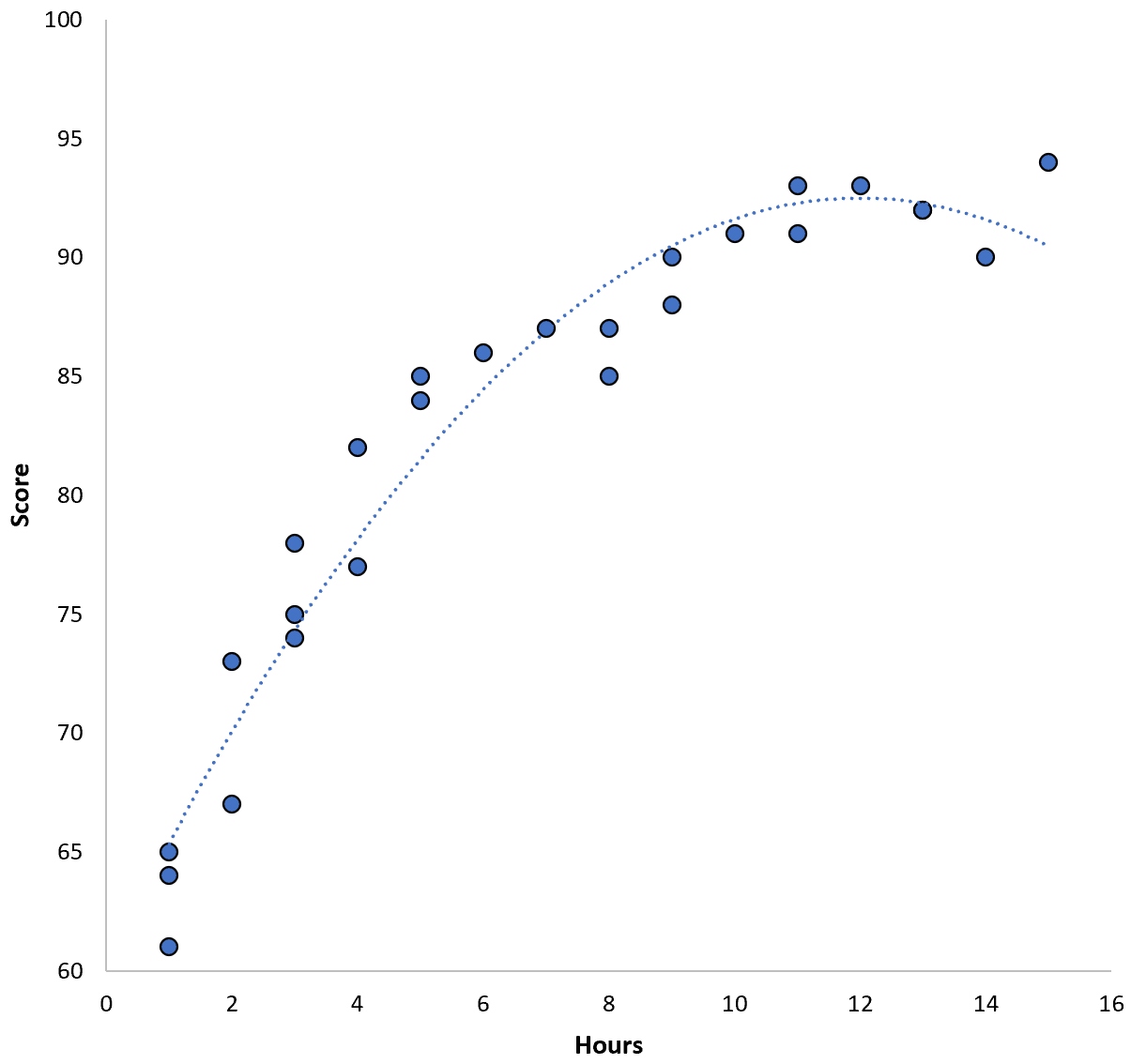
Este modelo tem um erro quadrático médio de treinamento (MSE) de 3,45 . Ou seja, a diferença quadrática média entre as previsões feitas pelo modelo e as pontuações reais do ACT é 3,45.
No entanto, poderíamos reduzir esse MSE de treinamento ajustando um modelo polinomial de ordem superior. Por exemplo, suponha que apliquemos o seguinte modelo:
Pontuação = 64,3 – 7,1*(Horas) + 8,1*(Horas) 2 – 2,1*(Horas) 3 + 0,2*(Horas ) 4 – 0,1*(Horas) 5 + 0,2(Horas) 6
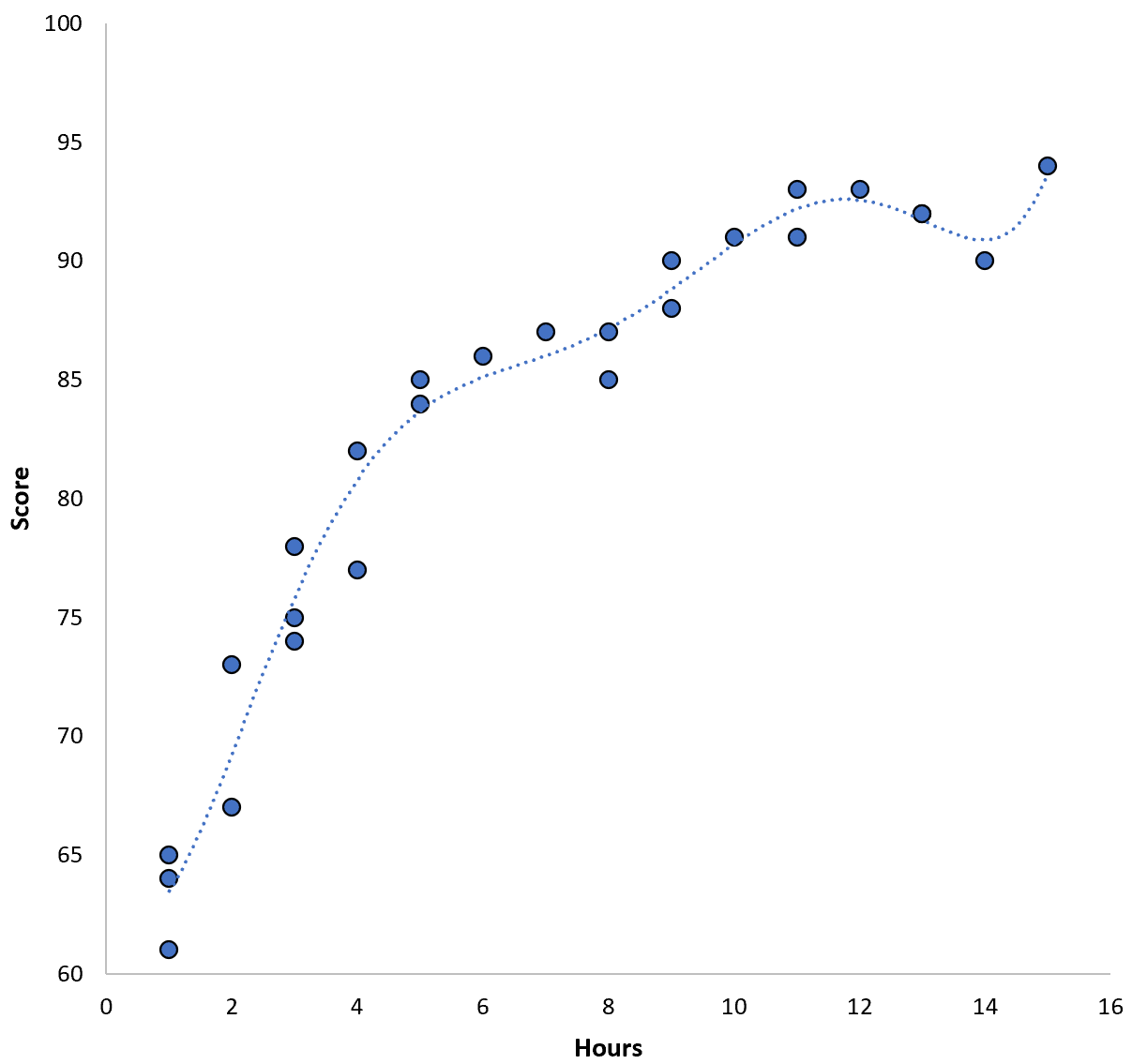
Observe como a linha de regressão se ajusta aos dados reais com muito mais precisão do que a linha de regressão anterior.
Este modelo tem um erro quadrático médio (MSE) de treinamento de apenas 0,89 . Ou seja, a diferença quadrática média entre as previsões feitas pelo modelo e as pontuações reais do ACT é 0,89.
Este treinamento MSE é muito menor que o produzido pelo modelo anterior.
No entanto, não nos importamos realmente com o MSE de treinamento , ou seja, quão bem as previsões do modelo correspondem aos dados que usamos para treinar o modelo. Em vez disso, preocupamo-nos principalmente com o teste MSE – o MSE quando o nosso modelo é aplicado a dados não vistos.
Se aplicássemos o modelo de regressão polinomial de ordem superior acima a um conjunto de dados invisível, provavelmente teria um desempenho pior do que o modelo de regressão quadrática mais simples. Ou seja, produziria um teste MSE mais alto, que é exatamente o que não queremos.
Como detectar e evitar overfitting
A maneira mais simples de detectar overfitting é realizar validação cruzada. O método mais comumente usado é conhecido como validação cruzada k-fold e funciona da seguinte forma:
Etapa 1: divida aleatoriamente um conjunto de dados em k grupos, ou “dobras”, de tamanho aproximadamente igual.

Passo 2: Escolha uma das dobras como conjunto de fixação. Ajuste o modelo às dobras k-1 restantes. Calcule o teste MSE nas observações da camada que foi tensionada.

Etapa 3: Repita esse processo k vezes, cada vez usando um conjunto diferente como conjunto de exclusão.

Etapa 4: Calcule o MSE geral do teste como a média dos k MSEs do teste.
Teste MSE = (1/k)*ΣMSE i
Ouro:
- k: Número de dobras
- MSE i : Teste MSE na i- ésima iteração
Este teste MSE nos dá uma boa ideia do desempenho de um determinado modelo em dados desconhecidos.
Na prática, podemos ajustar vários modelos diferentes e realizar validação cruzada k-fold em cada modelo para descobrir seu teste MSE. Podemos então escolher o modelo com o teste MSE mais baixo como o melhor modelo a ser usado para fazer previsões no futuro.
Isso garante que selecionemos um modelo que provavelmente terá melhor desempenho em dados futuros, em oposição a um modelo que simplesmente minimiza o MSE de treinamento e “se ajusta” bem aos dados históricos.
Recursos adicionais
Qual é a compensação entre viés e variância no aprendizado de máquina?
Uma introdução à validação cruzada K-Fold
Modelos de regressão e classificação em aprendizado de máquina