Regressão lasso em r (passo a passo)
A regressão laço é um método que podemos usar para ajustar um modelo de regressão quando a multicolinearidade está presente nos dados.
Resumindo, a regressão de mínimos quadrados tenta encontrar estimativas de coeficientes que minimizem a soma residual dos quadrados (RSS):
RSS = Σ(y i – ŷ i )2
Ouro:
- Σ : Um símbolo grego que significa soma
- y i : o valor real da resposta para a i-ésima observação
- ŷ i : O valor da resposta prevista com base no modelo de regressão linear múltipla
Por outro lado, a regressão laço procura minimizar o seguinte:
RSS + λΣ|β j |
onde j vai de 1 a p variáveis preditoras e λ ≥ 0.
Este segundo termo da equação é conhecido como penalidade de retirada . Na regressão laço, selecionamos um valor para λ que produz o teste MSE (erro quadrático médio) mais baixo possível.
Este tutorial fornece um exemplo passo a passo de como realizar uma regressão laço em R.
Etapa 1: carregar dados
Para este exemplo, usaremos o conjunto de dados integrado do R chamado mtcars . Usaremos hp como variável de resposta e as seguintes variáveis como preditores:
- mpg
- peso
- merda
- qsec
Para realizar a regressão laço, usaremos funções do pacote glmnet . Este pacote requer que a variável de resposta seja um vetor e que o conjunto de variáveis preditoras seja da classe data.matrix .
O código a seguir mostra como definir nossos dados:
#define response variable
y <- mtcars$hp
#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])
Etapa 2: ajustar o modelo de regressão Lasso
A seguir, usaremos a função glmnet() para ajustar o modelo de regressão laço e especificar alpha=1 .
Observe que definir alfa igual a 0 é equivalente a usar regressão de crista e definir alfa para um valor entre 0 e 1 é equivalente a usar uma rede elástica.
Para determinar qual valor usar para lambda, realizaremos a validação cruzada k-fold e identificaremos o valor lambda que produz o menor erro quadrático médio de teste (MSE).
Observe que a função cv.glmnet() executa automaticamente a validação cruzada k-fold usando k = 10 vezes.
library (glmnet)
#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )
#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda
[1] 5.616345
#produce plot of test MSE by lambda value
plot(cv_model)
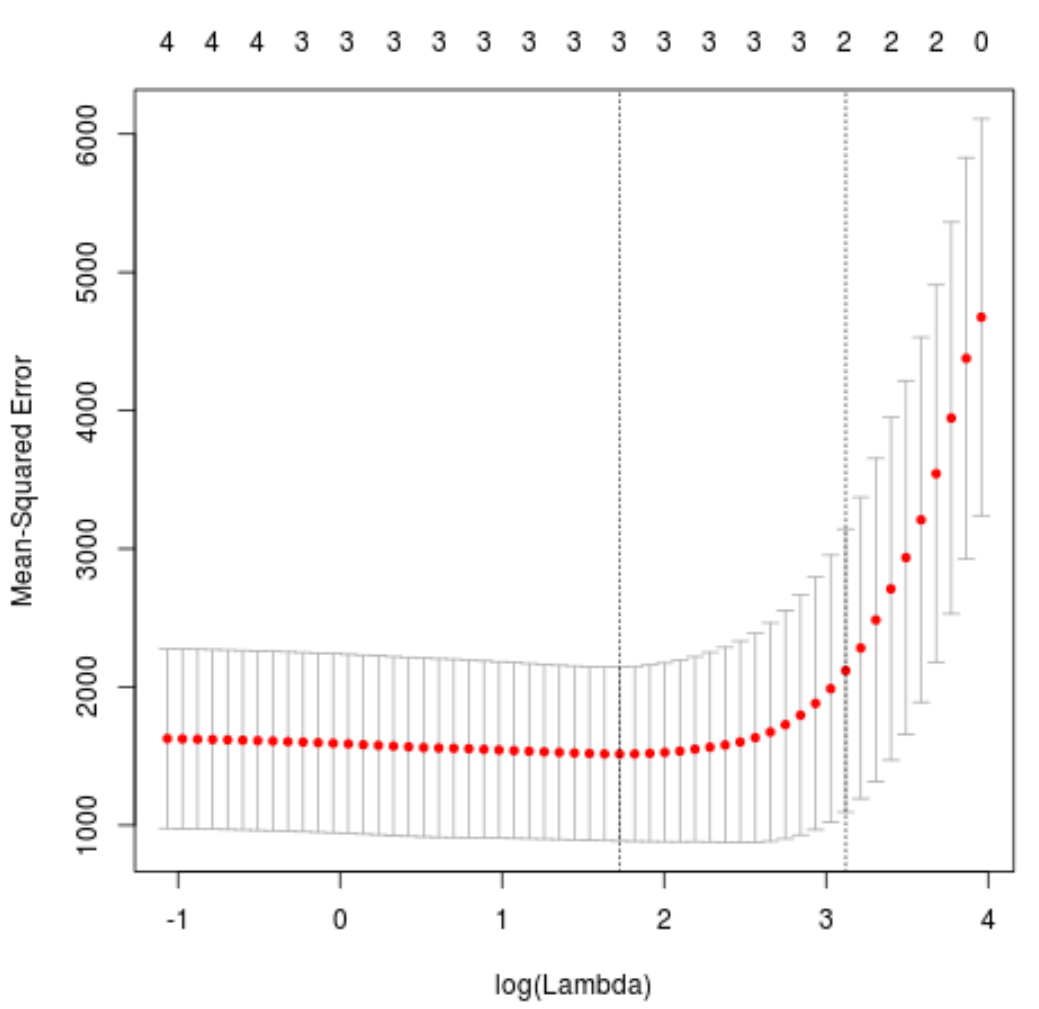
O valor lambda que minimiza o teste MSE é 5.616345 .
Etapa 3: Analise o modelo final
Finalmente, podemos analisar o modelo final produzido pelo valor lambda ótimo.
Podemos usar o seguinte código para obter as estimativas dos coeficientes para este modelo:
#find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.
qsec -19.43425
Nenhum coeficiente é mostrado para o preditor drat porque a regressão laço reduziu o coeficiente a zero. Isso significa que ele foi completamente afastado do modelo porque não tinha influência suficiente.
Observe que esta é uma diferença fundamental entre a regressão de crista e a regressão de laço . A regressão Ridge reduz todos os coeficientes a zero, mas a regressão laço tem o potencial de remover preditores do modelo, reduzindo os coeficientes completamente a zero.
Também podemos usar o modelo final de regressão laço para fazer previsões sobre novas observações. Por exemplo, suponha que temos um carro novo com os seguintes atributos:
- mpg: 24
- peso: 2,5
- preço: 3,5
- qseg: 18,5
O código a seguir mostra como usar o modelo de regressão laço ajustado para prever o valor hp desta nova observação:
#define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 )
#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)
[1,] 109.0842
Com base nos valores inseridos, o modelo prevê que este carro terá um valor de cv de 109,0842 .
Finalmente, podemos calcular o R-quadrado do modelo nos dados de treinamento:
#use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)
#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)
#find R-Squared
rsq <- 1 - sse/sst
rsq
[1] 0.8047064
O R ao quadrado é 0,8047064 . Ou seja, o melhor modelo foi capaz de explicar 80,47% da variação nos valores de resposta dos dados de treinamento.
Você pode encontrar o código R completo usado neste exemplo aqui .