Mle para uma distribuição de poisson (passo a passo)

A estimativa de máxima verossimilhança (MLE) é um método que pode ser usado para estimar os parâmetros de uma determinada distribuição.

Este tutorial explica como calcular o MLE para o parâmetro λ de uma distribuição de Poisson .

Etapa 1: Escreva o PDF.

Primeiro, escreva a função de densidade de probabilidade da distribuição de Poisson:

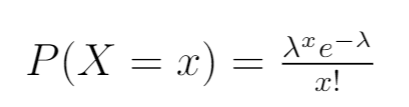
Etapa 2: Escreva a função de verossimilhança.

A seguir, escreva a função de verossimilhança. Este é simplesmente o produto da PDF para os valores observados x ₁ , …, x _n .

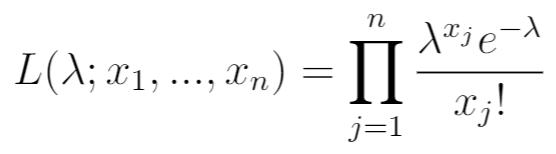
Etapa 3: Escreva a função de verossimilhança do logaritmo natural.

Para simplificar os cálculos, podemos escrever a função de verossimilhança natural:

Etapa 4: Calcule a derivada da função de verossimilhança natural em relação a λ.

Então podemos calcular a derivada da função de verossimilhança natural em relação ao parâmetro λ:

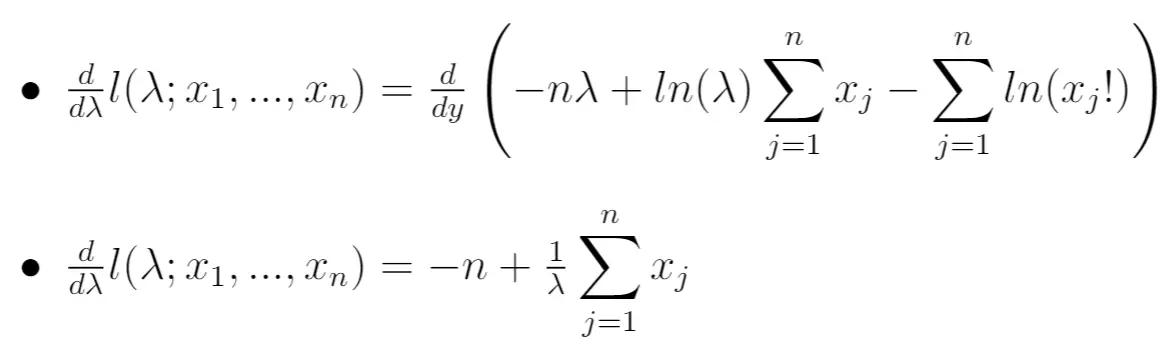
Etapa 5: Defina a derivada igual a zero e resolva λ.

Finalmente, definimos a derivada da etapa anterior igual a zero e simplesmente resolvemos para λ:

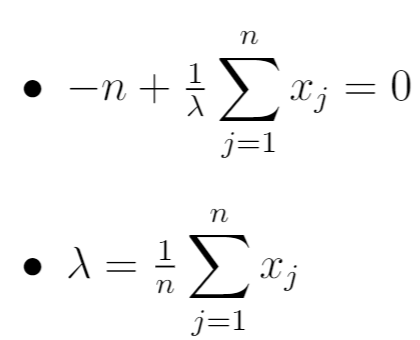
Assim, o MLE acaba sendo:

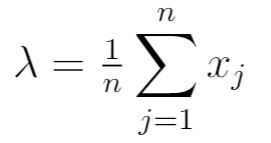
Isso é equivalente à média amostral das n observações na amostra.

Recursos adicionais

Uma introdução à distribuição de Poisson
Calculadora de distribuição de peixes
Como usar a distribuição de Poisson no Excel