Regressão de componentes principais em python (passo a passo)
Dado um conjunto de p variáveis preditoras e uma variável de resposta, a regressão linear múltipla usa um método conhecido como mínimos quadrados para minimizar a soma residual dos quadrados (RSS):
RSS = Σ(y i – ŷ i ) 2
Ouro:
- Σ : Um símbolo grego que significa soma
- y i : o valor real da resposta para a i-ésima observação
- ŷ i : O valor da resposta prevista com base no modelo de regressão linear múltipla
No entanto, quando as variáveis preditoras são altamente correlacionadas, a multicolinearidade pode se tornar um problema. Isso pode tornar as estimativas dos coeficientes do modelo pouco confiáveis e exibir alta variância.
Uma maneira de evitar esse problema é usar a regressão de componentes principais , que encontra M combinações lineares (chamadas de “componentes principais”) dos p preditores originais e, em seguida, usa mínimos quadrados para ajustar um modelo de regressão linear usando os componentes principais como preditores.
Este tutorial fornece um exemplo passo a passo de como realizar a regressão de componentes principais em Python.
Passo 1: Importe os pacotes necessários
Primeiro, importaremos os pacotes necessários para realizar a regressão de componentes principais (PCR) em Python:
import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn. PCA import decomposition
from sklearn. linear_model import LinearRegression
from sklearn. metrics import mean_squared_error
Etapa 2: carregar dados
Neste exemplo, usaremos um conjunto de dados chamado mtcars , que contém informações sobre 33 carros diferentes. Usaremos hp como variável de resposta e as seguintes variáveis como preditores:
- mpg
- mostrar
- merda
- peso
- qsec
O código a seguir mostra como carregar e exibir esse conjunto de dados:
#define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"
#read in data
data_full = pd. read_csv (url)
#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]
#view first six rows of data
data[0:6]
mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105
Passo 3: Ajustar o modelo PCR
O código a seguir mostra como ajustar o modelo PCR a esses dados. Observe o seguinte:
- pca.fit_transform(scale(X)) : Isso diz ao Python que cada uma das variáveis preditoras deve ser dimensionada para ter uma média de 0 e um desvio padrão de 1. Isso garante que nenhuma variável preditora tenha muita influência no modelo se isto ocorre. ser medido em unidades diferentes.
- cv = RepeatedKFold() : diz ao Python para usar a validação cruzada k-fold para avaliar o desempenho do modelo. Para este exemplo escolhemos k = 10 dobras, repetidas 3 vezes.
#define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]
#scale predictor variables
pca = pca()
X_reduced = pca. fit_transform ( scale (X))
#define cross validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )
regr = LinearRegression()
mse = []
# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (regr,
n.p. ones ((len(X_reduced),1)), y, cv=cv,
scoring=' neg_mean_squared_error '). mean ()
mse. append (score)
# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
score = -1*model_selection. cross_val_score (regr,
X_reduced[:,:i], y, cv=cv, scoring=' neg_mean_squared_error '). mean ()
mse. append (score)
# Plot cross-validation results
plt. plot (mse)
plt. xlabel ('Number of Principal Components')
plt. ylabel ('MSE')
plt. title ('hp')
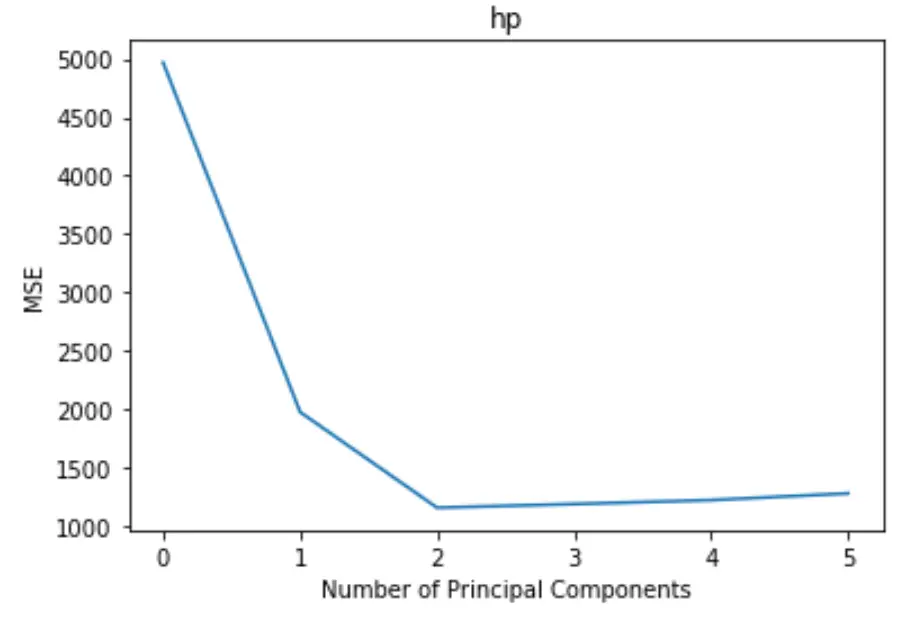
O gráfico exibe o número de componentes principais ao longo do eixo x e o teste MSE (erro quadrático médio) ao longo do eixo y.
No gráfico, podemos ver que o MSE do teste diminui ao adicionar dois componentes principais, mas começa a aumentar à medida que adicionamos mais de dois componentes principais.
Assim, o modelo ótimo inclui apenas os dois primeiros componentes principais.
Também podemos usar o código a seguir para calcular a porcentagem de variância na variável de resposta explicada pela adição de cada componente principal ao modelo:
n.p. cumsum (np. round (pca. explained_variance_ratio_ , decimals= 4 )* 100 )
array([69.83, 89.35, 95.88, 98.95, 99.99])
Podemos ver o seguinte:
- Utilizando apenas a primeira componente principal, podemos explicar 69,83% da variação da variável resposta.
- Adicionando o segundo componente principal, podemos explicar 89,35% da variação da variável resposta.
Observe que ainda seremos capazes de explicar mais variância usando mais componentes principais, mas podemos ver que adicionar mais de dois componentes principais não aumenta muito a porcentagem de variância explicada.
Etapa 4: use o modelo final para fazer previsões
Podemos usar o modelo final de PCR de dois componentes principais para fazer previsões sobre novas observações.
O código a seguir mostra como dividir o conjunto de dados original em um conjunto de treinamento e teste e usar o modelo PCR com dois componentes principais para fazer previsões no conjunto de teste.
#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size= 0.3 , random_state= 0 )
#scale the training and testing data
X_reduced_train = pca. fit_transform ( scale (X_train))
X_reduced_test = pca. transform ( scale (X_test))[:,:1]
#train PCR model on training data
regr = LinearRegression()
reg. fit (X_reduced_train[:,:1], y_train)
#calculate RMSE
pred = regr. predict (X_reduced_test)
n.p. sqrt ( mean_squared_error (y_test, pred))
40.2096
Vemos que o teste RMSE acabou sendo 40,2096 . Este é o desvio médio entre o valor de HP previsto e o valor de HP observado para as observações do conjunto de teste.
O código Python completo usado neste exemplo pode ser encontrado aqui .