Mínimos quadrados parciais em python (passo a passo)

Um dos problemas mais comuns que você encontrará no aprendizado de máquina é a multicolinearidade . Isso ocorre quando duas ou mais variáveis preditoras em um conjunto de dados estão altamente correlacionadas.

Quando isso acontece, um modelo pode ser capaz de ajustar bem um conjunto de dados de treinamento, mas pode ter um desempenho ruim em um novo conjunto de dados que nunca viu, porque se ajusta demais ao conjunto de dados de treinamento. conjunto de treinamento.

Uma maneira de contornar esse problema é usar um método chamado mínimos quadrados parciais , que funciona da seguinte maneira:

• Padronize variáveis preditoras e de resposta.
• Calcule M combinações lineares (chamadas de “componentes PLS”) das p variáveis preditoras originais que explicam uma quantidade significativa de variação tanto na variável de resposta quanto nas variáveis preditoras.
• Use o método dos mínimos quadrados para ajustar um modelo de regressão linear usando os componentes PLS como preditores.
• Use a validação cruzada k-fold para encontrar o número ideal de componentes PLS a serem mantidos no modelo.

Este tutorial fornece um exemplo passo a passo de como executar mínimos quadrados parciais em Python.

Passo 1: Importe os pacotes necessários

Primeiro, importaremos os pacotes necessários para realizar mínimos quadrados parciais em Python:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

Etapa 2: carregar dados

Neste exemplo, usaremos um conjunto de dados chamado mtcars , que contém informações sobre 33 carros diferentes. Usaremos hp como variável de resposta e as seguintes variáveis como preditores:

• mpg
• mostrar
• merda
• peso
• qsec

O código a seguir mostra como carregar e exibir esse conjunto de dados:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Etapa 3: Ajustar o modelo de mínimos quadrados parciais

O código a seguir mostra como ajustar o modelo PLS a esses dados.

Observe que cv = RepeatedKFold() diz ao Python para usar validação cruzada k-fold para avaliar o desempenho do modelo. Para este exemplo escolhemos k = 10 dobras, repetidas 3 vezes.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

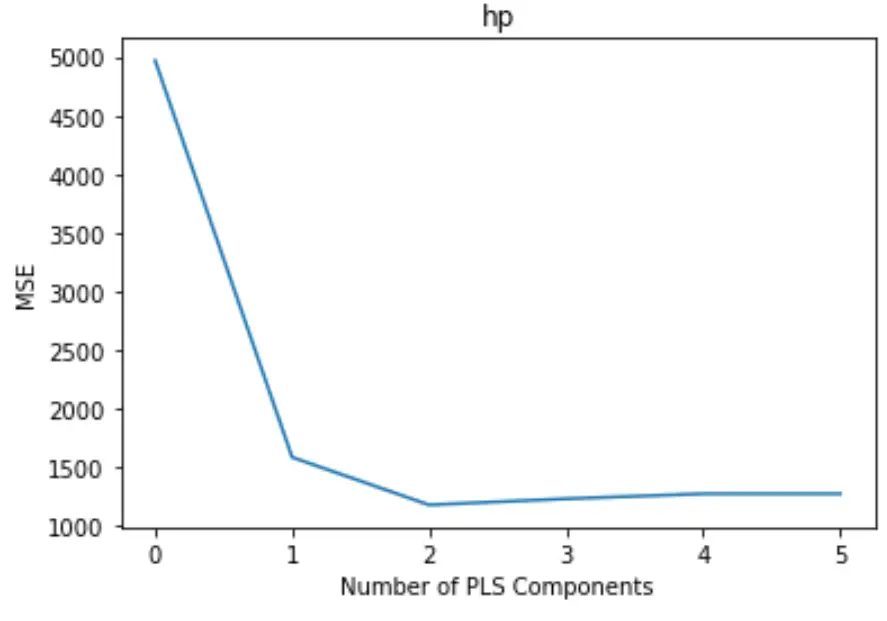
O gráfico exibe o número de componentes PLS ao longo do eixo x e o teste MSE (erro quadrático médio) ao longo do eixo y.

No gráfico, podemos ver que o MSE do teste diminui ao adicionar dois componentes do PLS, mas começa a aumentar à medida que adicionamos mais de dois componentes do PLS.

Assim, o modelo ótimo inclui apenas os dois primeiros componentes do PLS.

Etapa 4: use o modelo final para fazer previsões

Podemos usar o modelo PLS final com dois componentes PLS para fazer previsões sobre novas observações.

O código a seguir mostra como dividir o conjunto de dados original em um conjunto de treinamento e teste e usar o modelo PLS com dois componentes PLS para fazer previsões no conjunto de teste.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

Vemos que o RMSE do teste é 29,9094 . Este é o desvio médio entre o valor de HP previsto e o valor de HP observado para as observações do conjunto de teste.

O código Python completo usado neste exemplo pode ser encontrado aqui .