Uma introdução à regressão polinomial

Quando temos um conjunto de dados com uma variável preditora e uma variável de resposta , geralmente usamos regressão linear simples para quantificar a relação entre as duas variáveis.

No entanto, a regressão linear simples (SLR) assume que a relação entre o preditor e a variável de resposta é linear. Escrito em notação matemática, o SLR assume que o relacionamento assume a forma:

Y = β ₀ + β ₁ X + ε

Mas, na prática, a relação entre as duas variáveis pode, na verdade, ser não linear e a tentativa de utilizar a regressão linear pode resultar num modelo mal ajustado.

Uma maneira de explicar um relacionamento não linear entre o preditor e a variável de resposta é usar a regressão polinomial , que assume a forma:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² +… + β _h

Nesta equação, h é chamado de grau do polinômio.

À medida que aumentamos o valor de h , o modelo é capaz de acomodar melhor as relações não lineares, mas na prática raramente escolhemos h para ser maior que 3 ou 4. Além deste ponto, o modelo se torna muito flexível e superajusta os dados .

Notas técnicas

• Embora a regressão polinomial possa ajustar dados não lineares, ela ainda é considerada uma forma de regressão linear porque é linear nos coeficientes _β1 , _β2 ,…, _βh .
• A regressão polinomial também pode ser usada para múltiplas variáveis preditoras, mas isso cria termos de interação no modelo, o que pode tornar o modelo extremamente complexo se múltiplas variáveis preditoras forem usadas.

Quando usar regressão polinomial

Usamos regressão polinomial quando a relação entre um preditor e uma variável de resposta é não linear.

Existem três maneiras comuns de detectar um relacionamento não linear:

1. Crie um gráfico de dispersão.

A maneira mais simples de detectar um relacionamento não linear é criar um gráfico de dispersão da variável de resposta versus a variável preditora.

Por exemplo, se criarmos o gráfico de dispersão a seguir, podemos ver que a relação entre as duas variáveis é aproximadamente linear, portanto, uma regressão linear simples provavelmente funcionaria bem com esses dados.

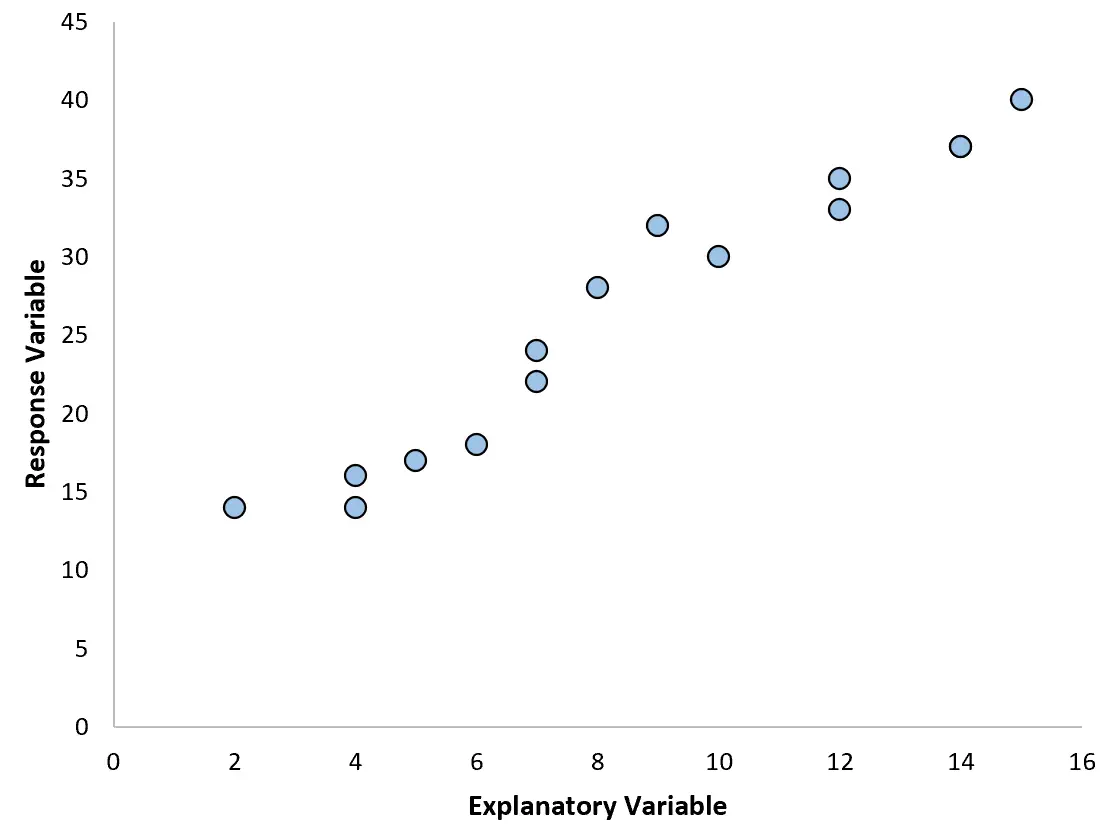
No entanto, se o nosso gráfico de dispersão se parecer com um dos gráficos a seguir, poderemos ver que a relação não é linear e, portanto, uma regressão polinomial seria uma boa ideia:

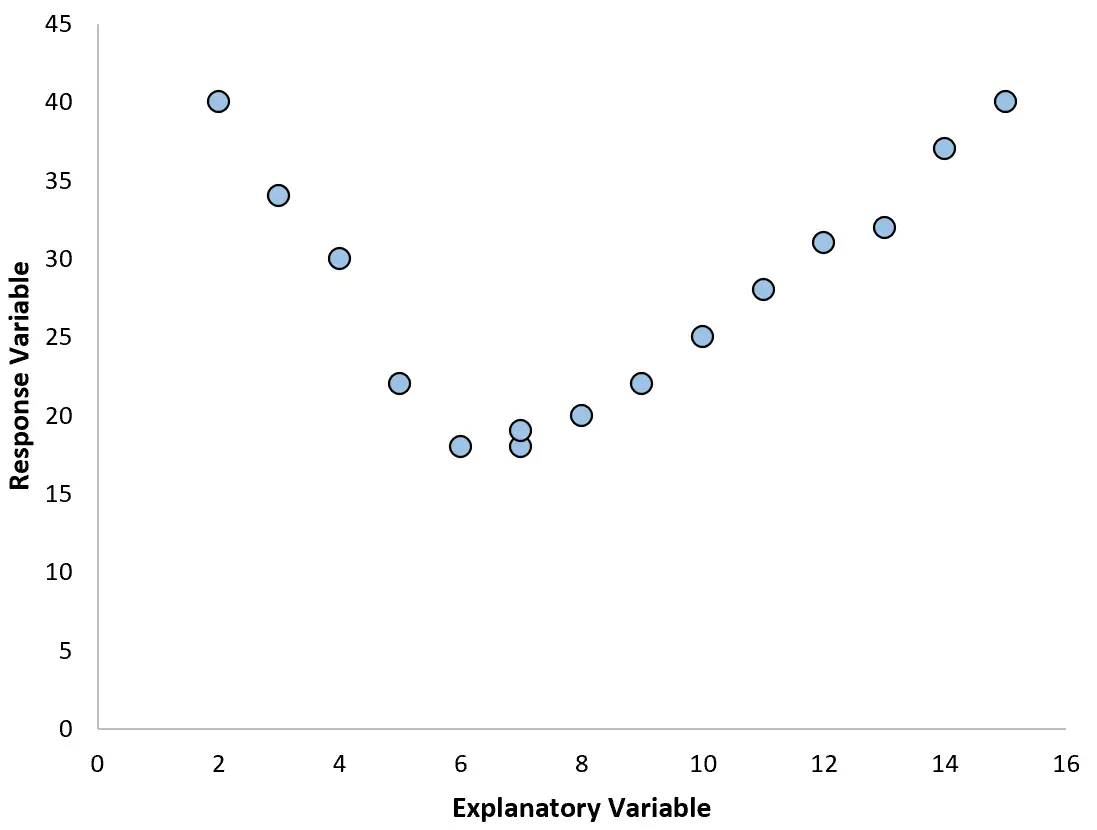
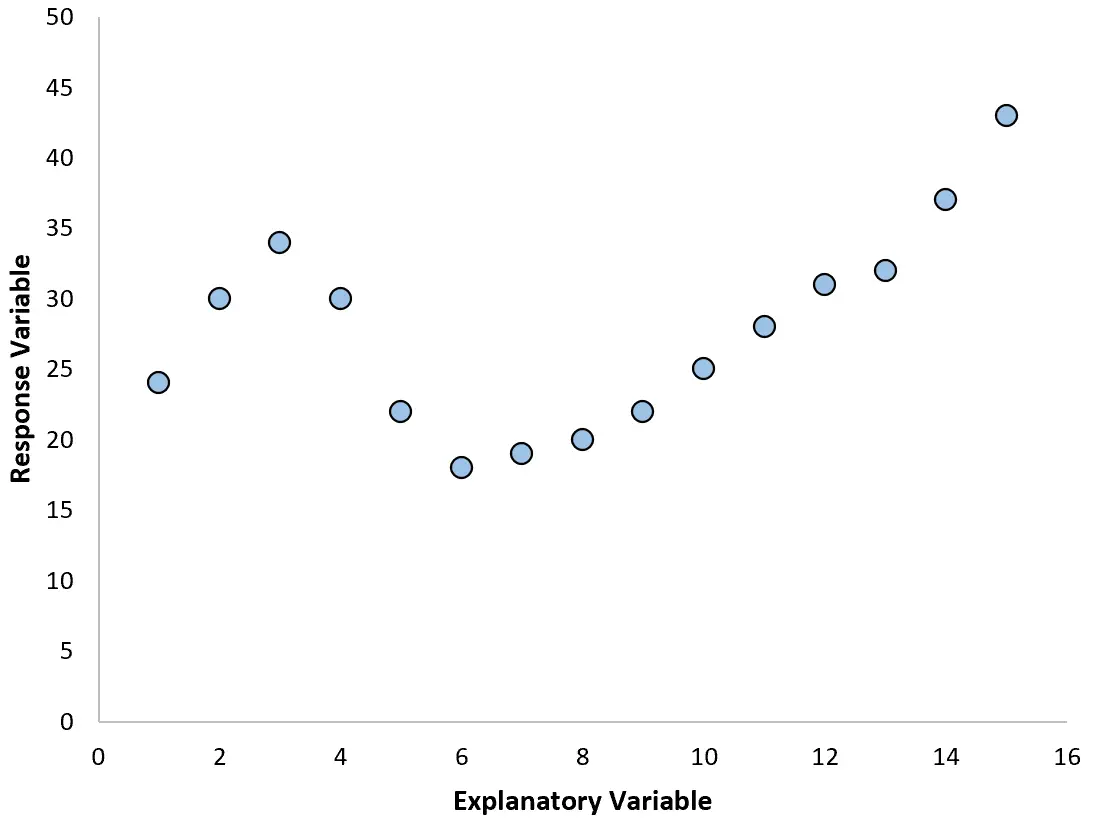
2. Crie um gráfico dos resíduos em relação ao gráfico ajustado.

Outra forma de detectar a não-linearidade é ajustar um modelo de regressão linear simples aos dados e depois produzir um gráfico dos resíduos em relação aos valores ajustados .

Se os resíduos do gráfico estiverem distribuídos aproximadamente uniformemente em torno de zero, sem nenhuma tendência clara, então a regressão linear simples é provavelmente suficiente.

No entanto, se os resíduos mostrarem uma tendência não linear no gráfico, isso indica que a relação entre o preditor e a resposta é provavelmente não linear.

3. Calcule o R ² do modelo.

O valor R ² de um modelo de regressão informa a porcentagem de variação na variável de resposta que pode ser explicada pela(s) variável(ões) preditora(s).

Se você ajustar um modelo de regressão linear simples a um conjunto de dados e o valor R ² do modelo for bastante baixo, isso poderá indicar que o relacionamento entre o preditor e a variável de resposta é mais complexo do que um relacionamento linear simples.

Isso pode ser um sinal de que talvez você precise tentar a regressão polinomial.

Relacionado: O que é um bom valor de R ao quadrado?

Como escolher o grau do polinômio

Um modelo de regressão polinomial assume a seguinte forma:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² +… + β _h

Nesta equação, h é o grau do polinômio.

Mas como escolher um valor para h ?

Na prática, ajustamos vários modelos diferentes com diferentes valores de h e realizamos validação cruzada k-fold para determinar qual modelo produz o menor erro quadrático médio de teste (MSE).

Por exemplo, podemos ajustar os seguintes modelos a um determinado conjunto de dados:

• Y = β ₀ + β ₁
• Y = β ₀ + β ₁ X + β ₂ X ²
• ^{Y =} _β0 + _β1X + _β2X2 + _β3X3
• Y = β ₀ + β ₁ X + β ₂ X ² + β ₃ X ³ + β ₄ X ⁴

Podemos então usar a validação cruzada k-fold para calcular o teste MSE para cada modelo, o que nos dirá o desempenho de cada modelo em dados que nunca viu antes.

A compensação entre viés e variância da regressão polinomial

Há uma compensação entre viés e variância ao usar a regressão polinomial. À medida que aumentamos o grau do polinômio, o viés diminui (à medida que o modelo se torna mais flexível), mas a variância aumenta.

Tal como acontece com todos os modelos de aprendizado de máquina, precisamos encontrar uma solução ideal entre viés e variância.

Na maioria dos casos isso permite que o grau do polinômio seja aumentado até certo ponto, mas além de um determinado valor o modelo começa a se adaptar ao ruído nos dados e o MSE do teste começa a diminuir.

Para garantir que ajustamos um modelo que seja flexível, mas não muito flexível, usamos a validação cruzada k-fold para encontrar o modelo que produz o teste MSE mais baixo.

Como realizar regressão polinomial

Os tutoriais a seguir fornecem exemplos de como realizar regressão polinomial em diferentes softwares:

Como realizar regressão polinomial no Excel
Como realizar regressão polinomial em R
Como realizar regressão polinomial em Python