Regressão linear múltipla manualmente (passo a passo)
A regressão linear múltipla é um método que podemos usar para quantificar a relação entre duas ou mais variáveis preditoras e uma variável de resposta .
Este tutorial explica como realizar manualmente a regressão linear múltipla.
Exemplo: regressão linear múltipla manualmente
Suponha que temos o seguinte conjunto de dados com uma variável de resposta y e duas variáveis preditoras x 1 e x 2 :
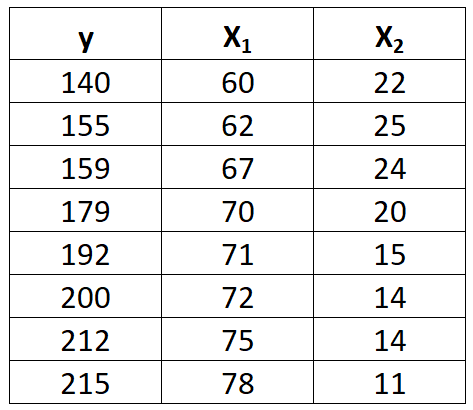
Conclua as etapas a seguir para ajustar um modelo de regressão linear múltipla a esse conjunto de dados.
Etapa 1: Calcule x 1 2 , x 2 2 , x 1 y, x 2 y e x 1 x 2 .
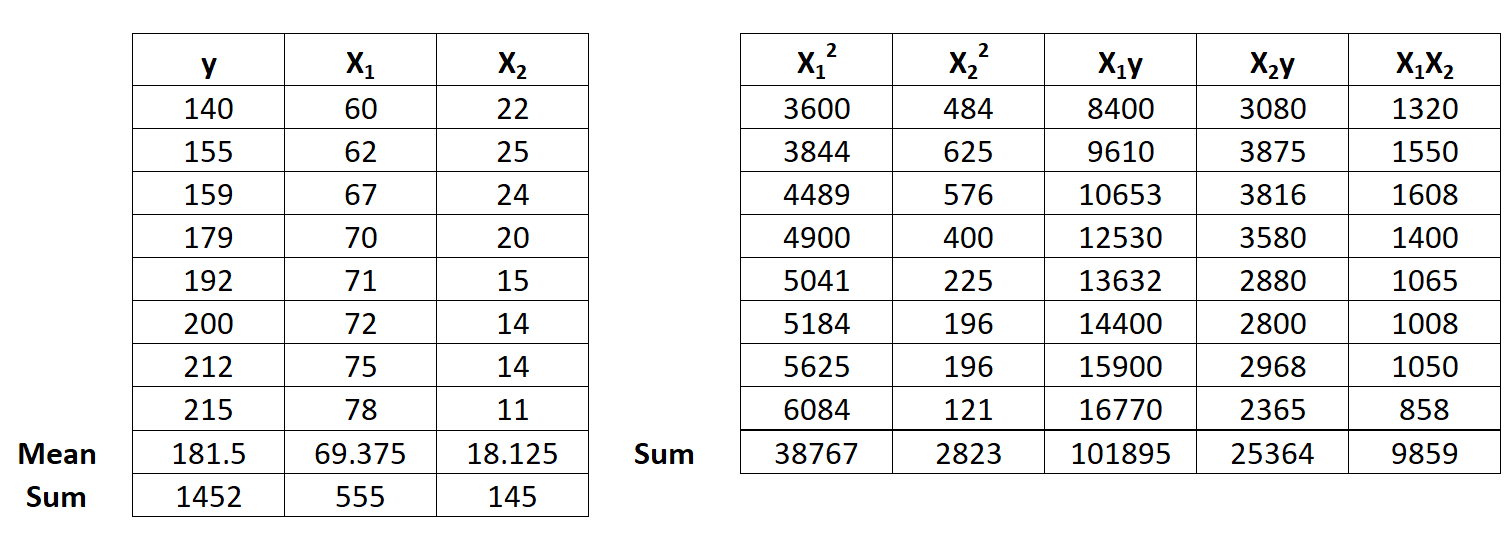
Etapa 2: Calcule as somas de regressão.
Em seguida, execute os seguintes cálculos de soma de regressão:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38,767 – (555) 2/8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2/8 = 194,875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
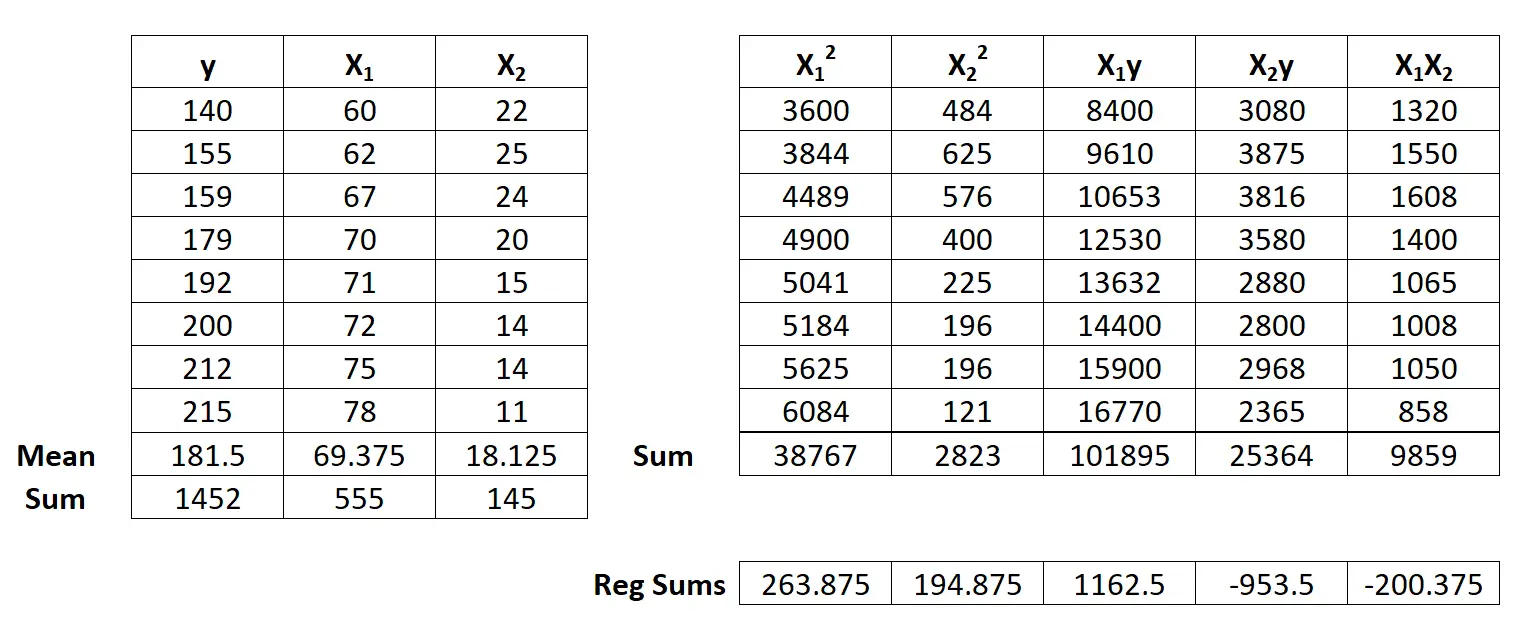
Etapa 3: Calcule b 0 , b 1 e b 2 .
A fórmula para calcular b 1 é: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Então, b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
A fórmula para calcular b 2 é: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Então, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
A fórmula para calcular b 0 é: y – b 1 X 1 – b 2 X 2
Assim, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Etapa 5: coloque b 0 , b 1 e b 2 na equação de regressão linear estimada.
A equação de regressão linear estimada é: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
Em nosso exemplo, é ŷ = -6,867 + 3,148x 1 – 1,656x 2
Como interpretar uma equação de regressão linear múltipla
Veja como interpretar esta equação de regressão linear estimada: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Quando ambas as variáveis preditoras são iguais a zero, o valor médio de y é -6,867.
b1 = 3,148 . Um aumento de uma unidade em x 1 está associado a um aumento de 3,148 unidades em y, em média, assumindo que x 2 permanece constante.
b2 = -1,656 . Um aumento de uma unidade em x 2 está associado a uma diminuição de 1.656 unidades em y, em média, assumindo que x 1 permanece constante.
Recursos adicionais
Uma introdução à regressão linear múltipla
Como realizar regressão linear simples manualmente