Splines de regressão adaptativa multivariada em r

Splines de regressão adaptativa multivariada (MARS) podem ser usadas para modelar relações não lineares entre um conjunto de variáveis preditoras e uma variável de resposta .

Este método funciona da seguinte maneira:

1. Divida um conjunto de dados em k partes.

2. Ajuste um modelo de regressão para cada parte.

3. Use a validação cruzada k-fold para escolher um valor para k .

Este tutorial fornece um exemplo passo a passo de como ajustar um modelo MARS a um conjunto de dados em R.

Passo 1: Carregue os pacotes necessários

Para este exemplo, usaremos o conjunto de dados ISLR Wage .   pacote, que contém os salários anuais de 3.000 pessoas, juntamente com uma variedade de variáveis preditoras, como idade, escolaridade, raça e muito mais.

Antes de ajustar um modelo MARS aos dados, carregaremos os pacotes necessários:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

Etapa 2: visualizar dados

A seguir, exibiremos as primeiras seis linhas do conjunto de dados com o qual estamos trabalhando:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

Etapa 3: Criar e otimizar o modelo MARS

A seguir, criaremos o modelo MARS para este conjunto de dados e realizaremos a validação cruzada k-fold para determinar qual modelo produz o menor teste RMSE (erro quadrático médio).

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

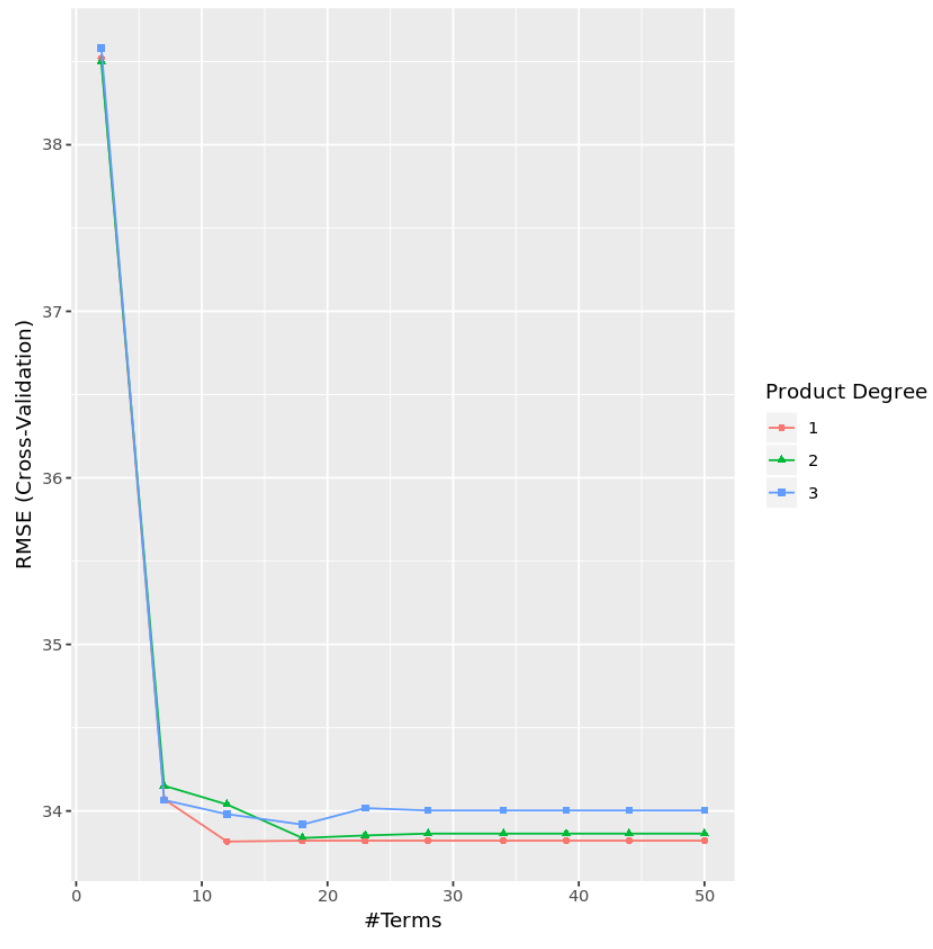
A partir dos resultados, podemos ver que o modelo que produziu o menor MSE de teste foi um modelo com apenas efeitos de primeira ordem (ou seja, sem termos de interação) e 12 termos. Este modelo produziu um erro quadrático médio (RMSE) de 33,8164 .

Nota: Usamos method=”earth” para especificar um modelo MARS. Você pode encontrar documentação para este método aqui .

Também podemos criar um gráfico para visualizar o teste RMSE com base no grau e na quantidade de termos:

 #display test RMSE by terms and degree
ggplot(cv_mars)

Na prática, adaptaríamos um modelo MARS com vários outros tipos de modelos como:

• Regressão linear múltipla
• Regressão polinomial
• Regressão de pico
• Regressão laço
• Regressão de componentes principais
• Mínimos quadrados parciais

Compararíamos então cada modelo para determinar qual leva ao menor erro de teste e escolheríamos esse modelo como o modelo ideal a ser usado.

O código R completo usado neste exemplo pode ser encontrado aqui .