Como calcular distribuições amostrais em r
Uma distribuição amostral é uma distribuição de probabilidade de uma determinada estatística baseada em muitas amostras aleatórias de uma única população.
Este tutorial explica como fazer o seguinte com distribuições de amostragem em R:
- Gere uma distribuição amostral.
- Visualize a distribuição amostral.
- Calcule a média e o desvio padrão da distribuição amostral.
- Calcule as probabilidades relativas à distribuição amostral.
Gere uma distribuição amostral em R
O código a seguir mostra como gerar uma distribuição amostral em R:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656
Neste exemplo, usamos a função rnorm() para calcular a média de 10.000 amostras em que cada tamanho de amostra era 20 e foi gerado a partir de uma distribuição normal com média de 5,3 e desvio padrão de 9.
Podemos ver que a primeira amostra teve média de 5,283992, a segunda amostra teve média de 6,304845 e assim por diante.
Visualize a distribuição amostral
O código a seguir mostra como criar um histograma simples para visualizar a distribuição da amostragem:
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
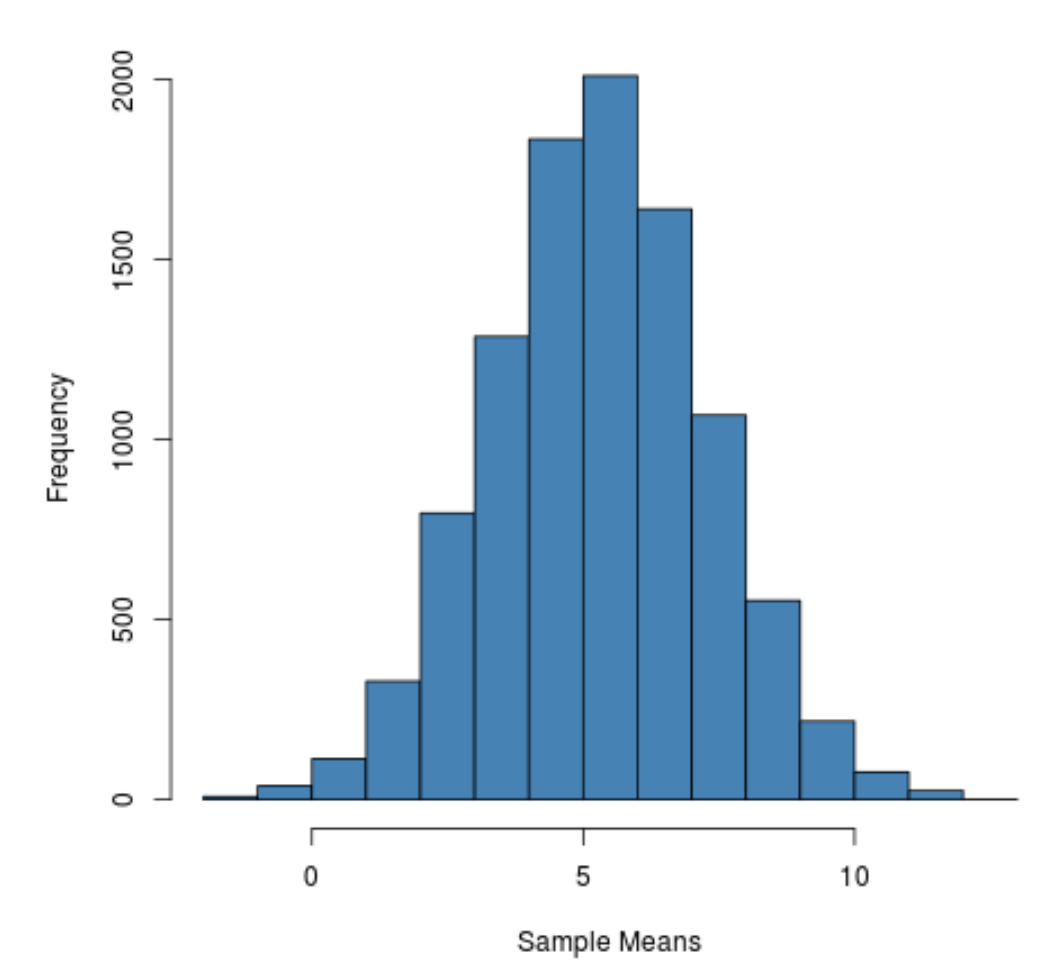
Pode-se observar que a distribuição amostral tem formato de sino com pico próximo ao valor 5.
Porém, pelas caudas da distribuição podemos ver que algumas amostras tiveram médias maiores que 10 e outras tiveram médias menores que 0.
Encontre a média e o desvio padrão
O código a seguir mostra como calcular a média e o desvio padrão da distribuição amostral:
#mean of sampling distribution
mean(sample_means)
[1] 5.287195
#standard deviation of sampling distribution
sd(sample_means)
[1] 2.00224
Teoricamente, a média da distribuição amostral deveria ser 5,3. Podemos ver que a média amostral real neste exemplo é 5,287195 , que é próxima de 5,3.
E teoricamente, o desvio padrão da distribuição amostral deveria ser igual a s/√n, que seria 9 / √20 = 2,012. Podemos ver que o desvio padrão real da distribuição amostral é 2,00224 , que é próximo de 2,012.
Calcule as probabilidades
O código a seguir mostra como calcular a probabilidade de obter um determinado valor para uma média amostral, dada uma média populacional, o desvio padrão populacional e o tamanho da amostra.
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
Neste exemplo específico, encontramos a probabilidade de a média da amostra ser menor ou igual a 6, dado que a média da população é 5,3, o desvio padrão da população é 9 e o tamanho da amostra de 20 é 0,6417 .
Isso está muito próximo da probabilidade calculada pela Calculadora de Distribuição de Amostragem :

O código completo
O código R completo usado neste exemplo é mostrado abaixo:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
#mean of sampling distribution
mean(sample_means)
#standard deviation of sampling distribution
sd(sample_means)
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
Recursos adicionais
Uma introdução às distribuições de amostragem
Calculadora de distribuição de amostragem
Uma introdução ao teorema do limite central