Como calcular distribuições de amostragem no excel
Uma distribuição amostral é uma distribuição de probabilidade de uma determinada estatística baseada em muitas amostras aleatórias de uma única população .
Este tutorial explica como fazer o seguinte com distribuições de amostragem no Excel:
- Gere uma distribuição amostral.
- Visualize a distribuição amostral.
- Calcule a média e o desvio padrão da distribuição amostral.
- Calcule as probabilidades relativas à distribuição amostral.
Gere uma distribuição amostral no Excel
Suponha que queiramos gerar uma distribuição amostral composta por 1.000 amostras em que cada tamanho de amostra seja 20 e venha de uma distribuição normal com média de 5,3 e desvio padrão de 9 .
Podemos fazer isso facilmente digitando a seguinte fórmula na célula A2 de nossa planilha:
= NORM . INV ( RAND (), 5.3, 9)
Podemos então passar o mouse sobre o canto inferior direito da célula até que um pequeno + apareça e arrastar a fórmula para a direita 20 células e para baixo 1000 células:
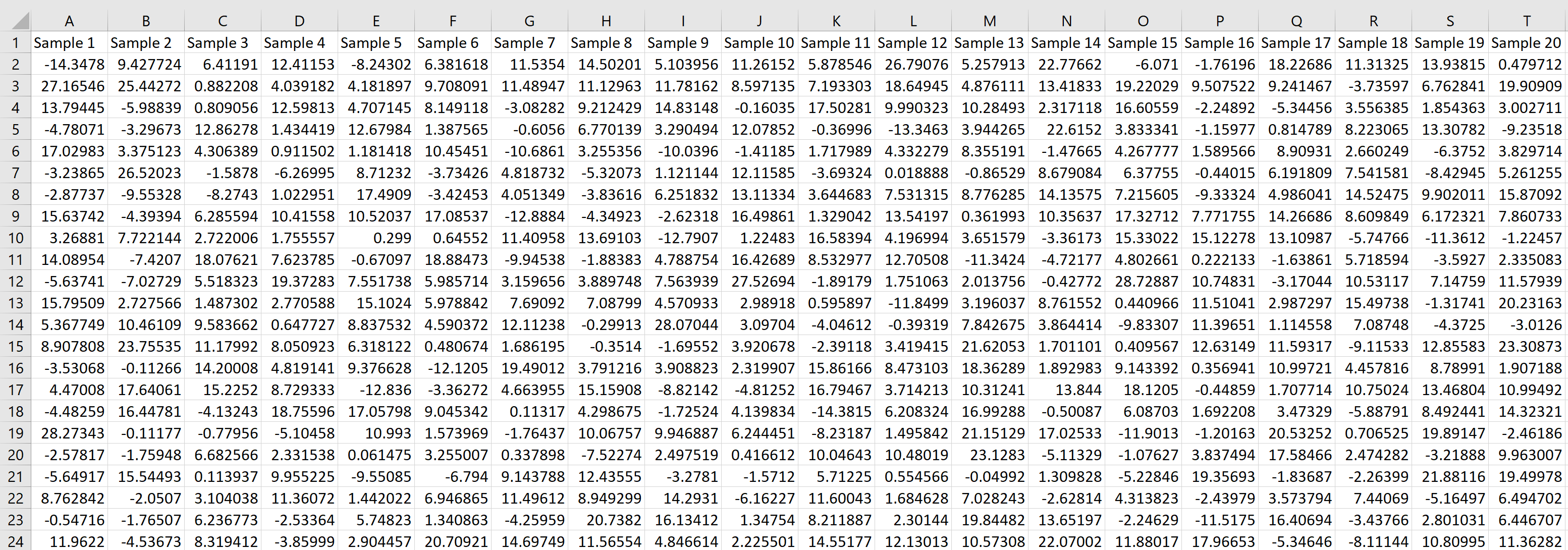
Cada linha representa uma amostra de tamanho 20 em que cada valor vem de uma distribuição normal com média de 5,3 e desvio padrão de 9.
Encontre a média e o desvio padrão
Para encontrar a média e o desvio padrão desta distribuição amostral das médias amostrais, podemos primeiro encontrar a média de cada amostra digitando a seguinte fórmula na célula U2 de nossa planilha:
= AVERAGE (A2:T2)
Podemos então passar o mouse sobre o canto inferior direito da célula até que um pequeno + apareça e clicar duas vezes para copiar esta fórmula para todas as outras células na coluna U:
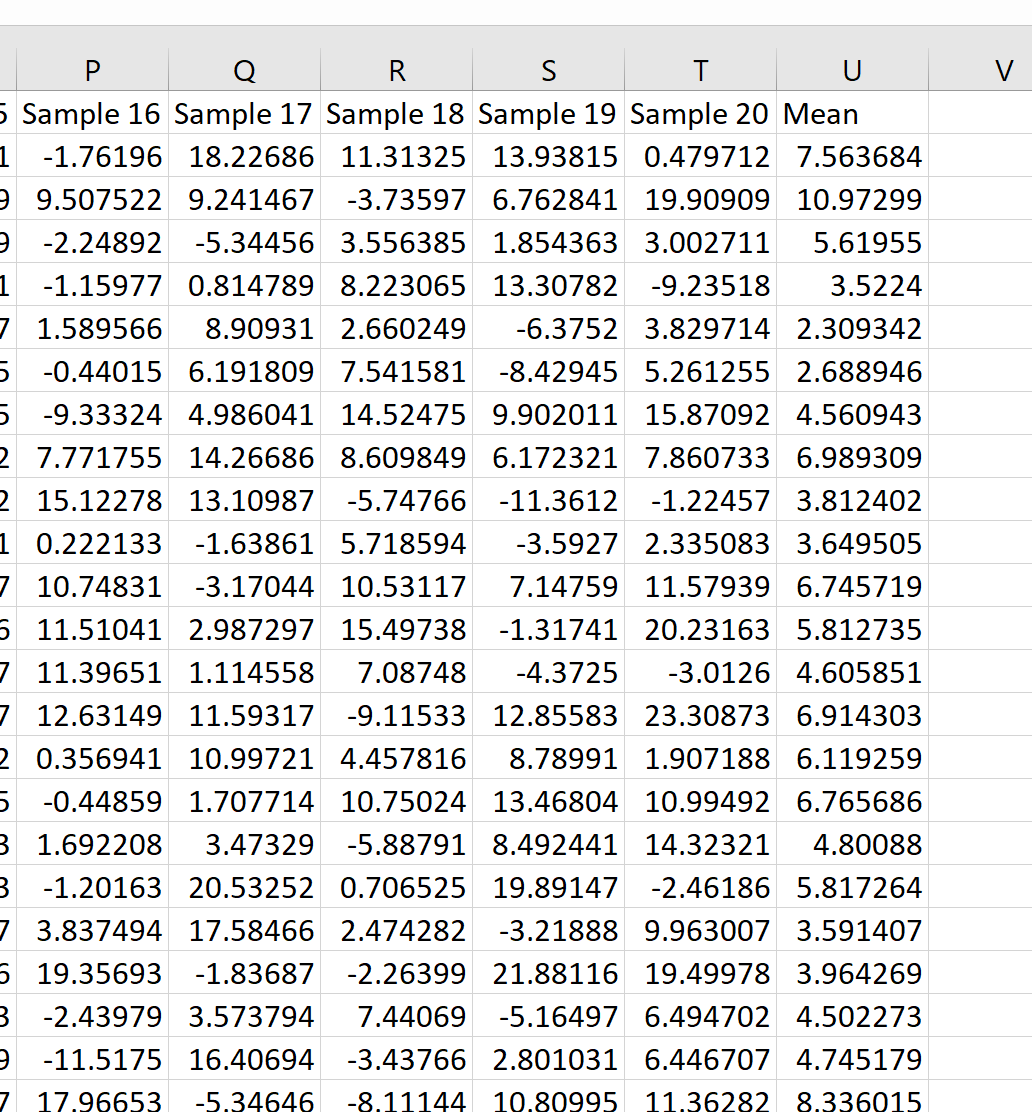
Podemos ver que a primeira amostra teve média de 7,563684, a segunda amostra teve média de 10,97299 e assim por diante.
Podemos então usar as seguintes fórmulas para calcular a média e o desvio padrão das médias amostrais:
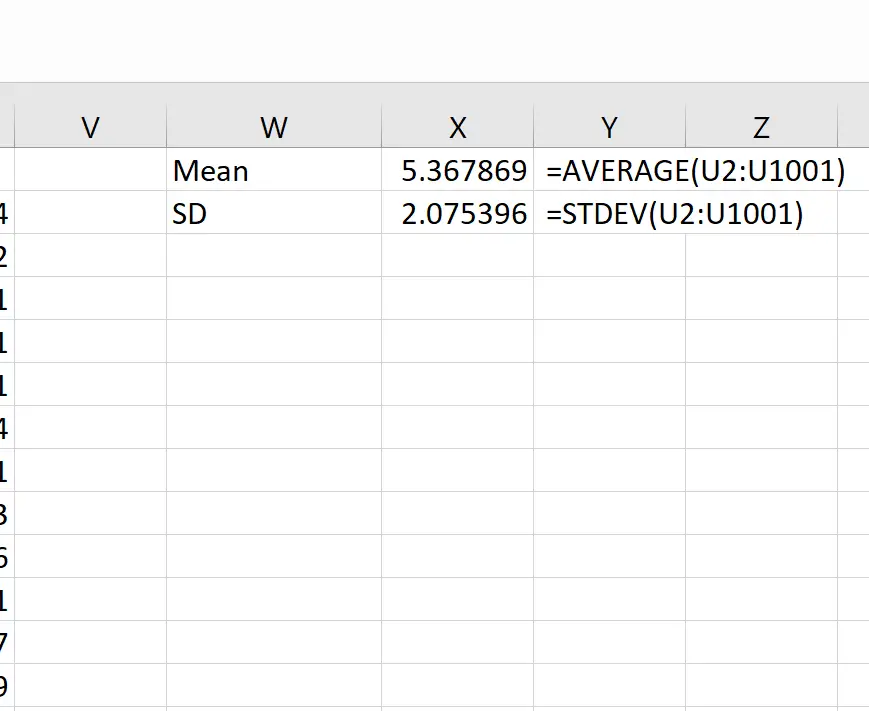
Teoricamente, a média da distribuição amostral deveria ser 5,3. Podemos ver que a média amostral real neste exemplo é 5,367869 , que é próxima de 5,3.
E teoricamente, o desvio padrão da distribuição amostral deveria ser igual a s/√n, que seria 9 / √20 = 2,012. Podemos ver que o desvio padrão real da distribuição amostral é 2,075396 , que é próximo de 2,012.
Visualize a distribuição amostral
Também podemos criar um histograma simples para visualizar a distribuição amostral das médias amostrais.
Para fazer isso, basta destacar todas as médias da amostra na coluna U, clicar na guia Inserir e, em seguida, clicar na opção Histograma na seção Gráficos .
Isso fornece o seguinte histograma:
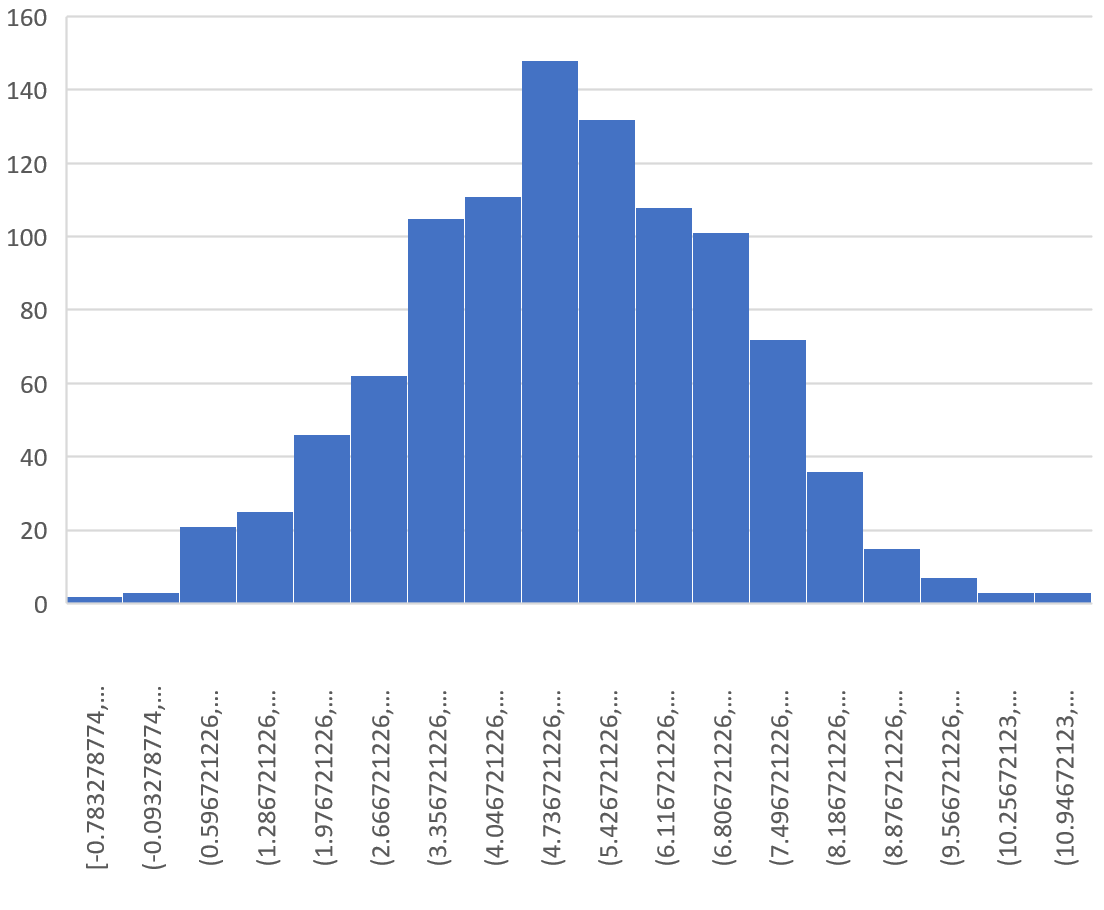
Pode-se observar que a distribuição amostral tem formato de sino com pico próximo ao valor 5.
Porém, pelas caudas da distribuição podemos ver que algumas amostras tiveram médias maiores que 10 e outras tiveram médias menores que 0.
Calcule as probabilidades
Também podemos calcular a probabilidade de obter um determinado valor para uma média amostral, com base na média populacional, no desvio padrão populacional e no tamanho da amostra.
Por exemplo, podemos usar a seguinte fórmula para encontrar a probabilidade de a média da amostra ser menor ou igual a 6, dado que a média da população é 5,3, o desvio padrão da população é 9 e o tamanho da amostra é:
= COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)
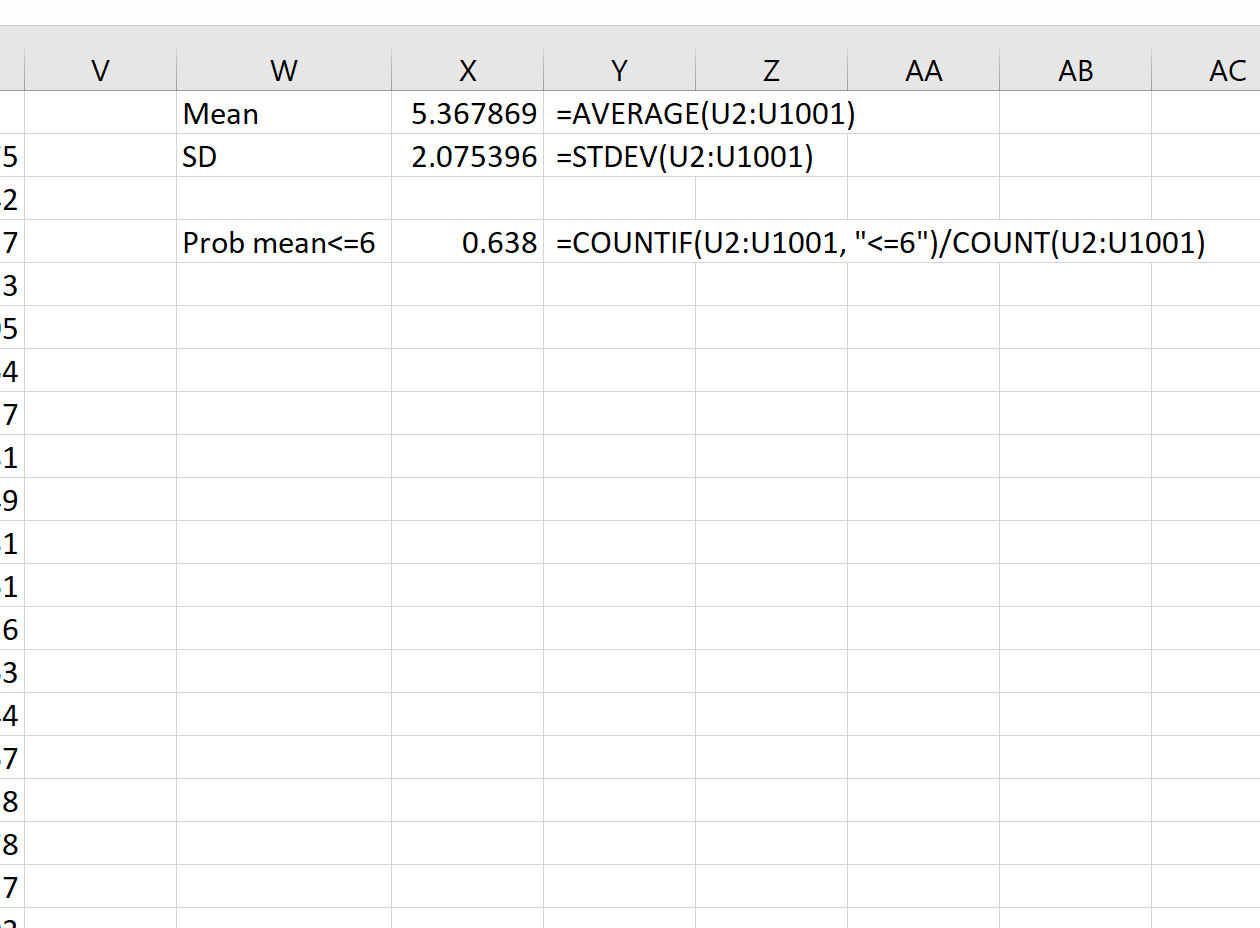
Vemos que a probabilidade de a média da amostra ser menor ou igual a 6 é 0,638.
Isso está muito próximo da probabilidade calculada pela Calculadora de Distribuição de Amostragem :

Recursos adicionais
Uma introdução às distribuições de amostragem
Calculadora de distribuição de amostragem
Uma introdução ao teorema do limite central