K-medoids em r: exemplo passo a passo

Clustering é uma técnica de aprendizado de máquina que tenta encontrar grupos ou clusters de observações dentro de um conjunto de dados.

O objetivo é encontrar clusters tais que as observações dentro de cada cluster sejam bastante semelhantes entre si, enquanto as observações em diferentes clusters sejam bastante diferentes umas das outras.

Clustering é uma forma de aprendizagem não supervisionada porque estamos simplesmente tentando encontrar uma estrutura dentro de um conjunto de dados, em vez de prever o valor de uma variável de resposta .

O clustering é frequentemente usado em marketing quando as empresas têm acesso a informações como:

• Renda familiar
• Tamanho da família
• Profissão de chefe de família
• Distância até a área urbana mais próxima

Quando esta informação está disponível, o agrupamento pode ser utilizado para identificar agregados familiares que são semelhantes e podem ter maior probabilidade de comprar determinados produtos ou responder melhor a um determinado tipo de publicidade.

Uma das formas mais comuns de agrupamento é conhecida como agrupamento k-means .

Infelizmente, esse método pode ser influenciado por outliers, e é por isso que uma alternativa frequentemente usada é o agrupamento k-medoids .

O que é agrupamento K-Medoids?

O agrupamento K-medoids é uma técnica na qual colocamos cada observação em um conjunto de dados em um dos K clusters.

O objetivo final é ter K clusters nos quais as observações dentro de cada cluster sejam bastante semelhantes entre si, enquanto as observações em diferentes clusters sejam bastante diferentes umas das outras.

Na prática, usamos as seguintes etapas para realizar o agrupamento K-means:

1. Escolha um valor para K.

• Primeiro, precisamos decidir quantos clusters queremos identificar nos dados. Muitas vezes precisamos simplesmente testar vários valores diferentes para K e analisar os resultados para ver qual número de clusters parece fazer mais sentido para um determinado problema.

2. Atribua aleatoriamente cada observação a um cluster inicial, de 1 a K.

3. Execute o procedimento a seguir até que as atribuições do cluster parem de mudar.

• Para cada um dos K clusters, calcule o centro de gravidade do cluster. Este é o vetor das p medianas das feições para as observações do k- ésimo cluster.
• Atribua cada observação ao cluster com o centróide mais próximo. Aqui, o mais próximo é definido usando a distância euclidiana .

Nota técnica:

Como k-medoids calcula centróides de cluster usando medianas em vez de médias, ele tende a ser mais robusto para valores discrepantes do que k-means.

Na prática, se não houver valores discrepantes extremos no conjunto de dados, k-means e k-medoids produzirão resultados semelhantes.

Agrupamento de K-Medoids em R

O tutorial a seguir fornece um exemplo passo a passo de como realizar clustering de k-medoids em R.

Passo 1: Carregue os pacotes necessários

Primeiro, carregaremos dois pacotes contendo diversas funções úteis para clusterização de k-medoids em R.

 library (factoextra)
library (cluster)

Etapa 2: carregar e preparar dados

Para este exemplo, usaremos o conjunto de dados USArrests incorporado em R, que contém o número de prisões por 100.000 pessoas em cada estado dos EUA em 1973 por assassinato , agressão e estupro , bem como a porcentagem da população de cada estado vivendo em áreas urbanas. áreas. , UrbanPop .

O código a seguir mostra como fazer o seguinte:

• Carregar conjunto de dados USArrests
• Remova todas as linhas com valores ausentes
• Dimensione cada variável no conjunto de dados para ter uma média de 0 e um desvio padrão de 1

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Etapa 3: Encontre o número ideal de clusters

Para realizar clustering k-medoid em R, podemos usar a função pam() , que significa “particionamento em torno de medianas” e usa a seguinte sintaxe:

pam(dados, k, métrica = “Euclidiano”, stand = FALSE)

Ouro:

• dados: nome do conjunto de dados.
• k: O número de clusters.
• métrica: a métrica a ser usada para calcular a distância. O padrão é euclidiano , mas você também pode especificar Manhattan .
• stand: se deve ou não normalizar cada variável no conjunto de dados. O valor padrão é falso.

Como não sabemos antecipadamente qual número de clusters é ideal, criaremos dois gráficos diferentes que podem nos ajudar a decidir:

1. Número de clusters em relação ao total na soma dos quadrados

Primeiro, usaremos a função fviz_nbclust() para criar um gráfico do número de clusters versus o total na soma dos quadrados:

 fviz_nbclust(df, pam, method = “ wss ”) 

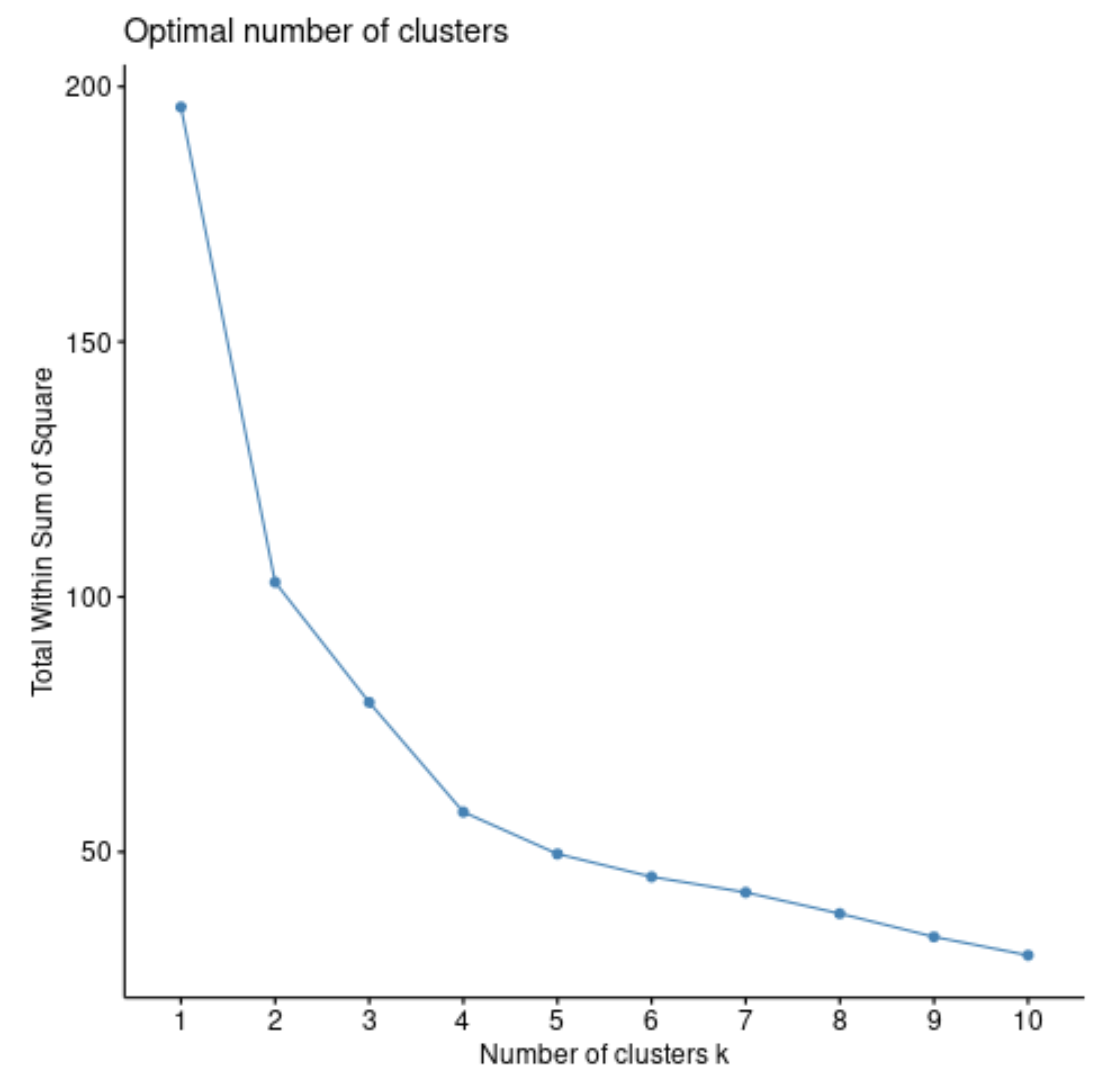
O total na soma dos quadrados geralmente sempre aumentará à medida que aumentamos o número de clusters. Portanto, quando criamos esse tipo de gráfico, procuramos um “joelho” onde a soma dos quadrados começa a “dobrar” ou se nivelar.

O ponto de curvatura do gráfico geralmente corresponde ao número ideal de clusters. Além deste valor, é provável que ocorra overfitting .

Para este gráfico, parece que há uma pequena torção ou “curvatura” em k = 4 clusters.

2. Número de clusters versus estatísticas de lacunas

Outra forma de determinar o número ideal de clusters é usar uma métrica chamada estatística de desvio , que compara a variação total intra-cluster para diferentes valores de k com seus valores esperados para uma distribuição sem cluster.

Podemos calcular a estatística de lacuna para cada número de clusters usando a função clusGap() do pacote de cluster , bem como um gráfico dos clusters versus estatísticas de lacuna usando a função fviz_gap_stat() :

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = pam,
                    K.max = 10, #max clusters to consider
                    B = 50) #total bootstrapped iterations

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

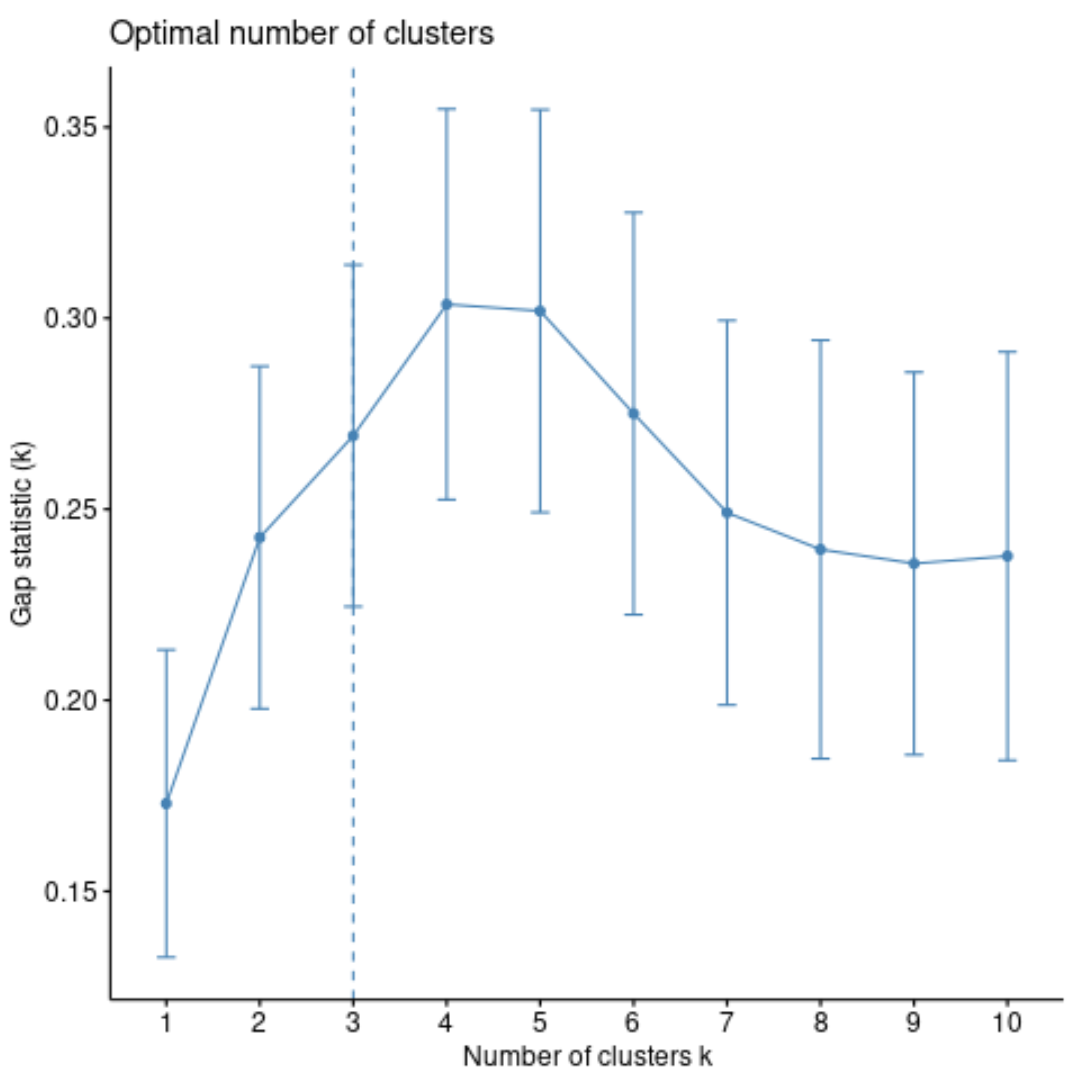
No gráfico, podemos ver que a estatística de gap é mais alta em k = 4 clusters, o que corresponde ao método do cotovelo que usamos anteriormente.

Etapa 4: realizar clustering K-Medoids com Optimal K

Finalmente, podemos realizar agrupamento de k-medóides no conjunto de dados usando o valor ideal para k de 4:

 #make this example reproducible
set.seed(1)

#perform k-medoids clustering with k = 4 clusters
kmed <- pam(df, k = 4)

#view results
kmed

              ID Murder Assault UrbanPop Rape
Alabama 1 1.2425641 0.7828393 -0.5209066 -0.003416473
Michigan 22 0.9900104 1.0108275 0.5844655 1.480613993
Oklahoma 36 -0.2727580 -0.2371077 0.1699510 -0.131534211
New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
Vector clustering:
       Alabama Alaska Arizona Arkansas California 
             1 2 2 1 2 
      Colorado Connecticut Delaware Florida Georgia 
             2 3 3 2 1 
        Hawaii Idaho Illinois Indiana Iowa 
             3 4 2 3 4 
        Kansas Kentucky Louisiana Maine Maryland 
             3 3 1 4 2 
 Massachusetts Michigan Minnesota Mississippi Missouri 
             3 2 4 1 3 
       Montana Nebraska Nevada New Hampshire New Jersey 
             3 3 2 4 3 
    New Mexico New York North Carolina North Dakota Ohio 
             2 2 1 4 3 
      Oklahoma Oregon Pennsylvania Rhode Island South Carolina 
             3 3 3 3 1 
  South Dakota Tennessee Texas Utah Vermont 
             4 1 2 3 4 
      Virginia Washington West Virginia Wisconsin Wyoming 
             3 3 4 4 3 
Objective function:
   build swap 
1.035116 1.027102 

Available components:
 [1] "medoids" "id.med" "clustering" "objective" "isolation" 
 [6] "clusinfo" "silinfo" "diss" "call" "data"          

Observe que todos os quatro centróides do cluster são observações reais no conjunto de dados. Perto do topo da saída, podemos ver que os quatro centróides são os seguintes estados:

• Alabama
• Michigan
• Oklahoma
• Nova Hampshire

Podemos visualizar os clusters em um gráfico de dispersão que exibe os dois primeiros componentes principais nos eixos usando a função fivz_cluster() :

 #plot results of final k-medoids model
fviz_cluster(kmed, data = df)

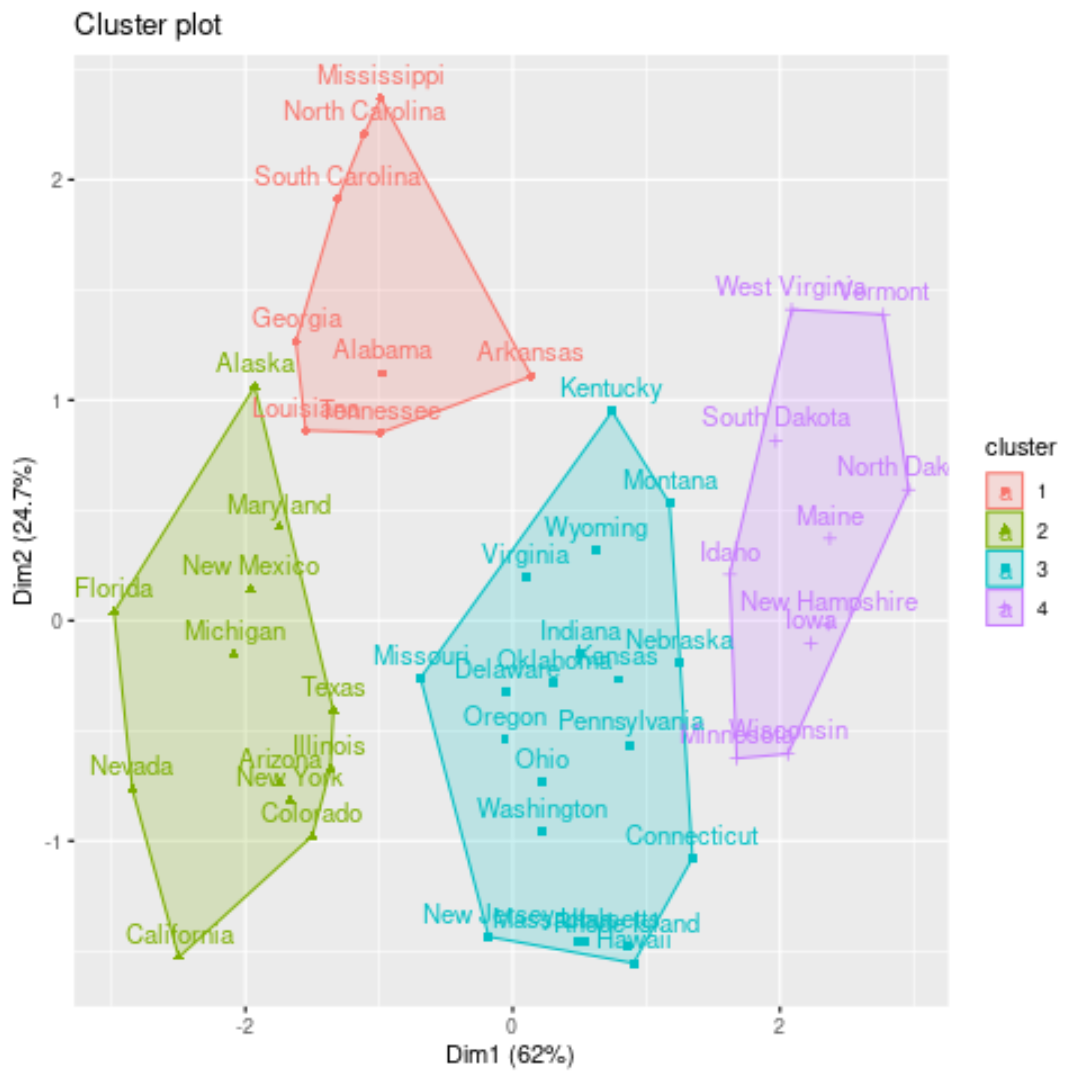
Também podemos adicionar as atribuições de cluster de cada estado ao conjunto de dados original:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = kmed$cluster)

#view final data
head(final_data)

           Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 1
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 1
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Você pode encontrar o código R completo usado neste exemplo aqui .