Como realizar uma transformação box-cox em python

Uma transformação box-cox é um método comumente usado para transformar um conjunto de dados distribuído não normalmente em um conjunto distribuído mais normalmente .

A ideia básica por trás deste método é encontrar um valor para λ tal que os dados transformados estejam o mais próximo possível da distribuição normal, usando a seguinte fórmula:

• y(λ) = (y ^λ – 1) / λ se y ≠ 0
• y(λ) = log(y) se y = 0

Podemos realizar uma transformação box-cox em Python usando a função scipy.stats.boxcox() .

O exemplo a seguir mostra como usar esta função na prática.

Exemplo: transformação Box-Cox em Python

Suponha que geramos um conjunto aleatório de 1.000 valores a partir de uma distribuição exponencial :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

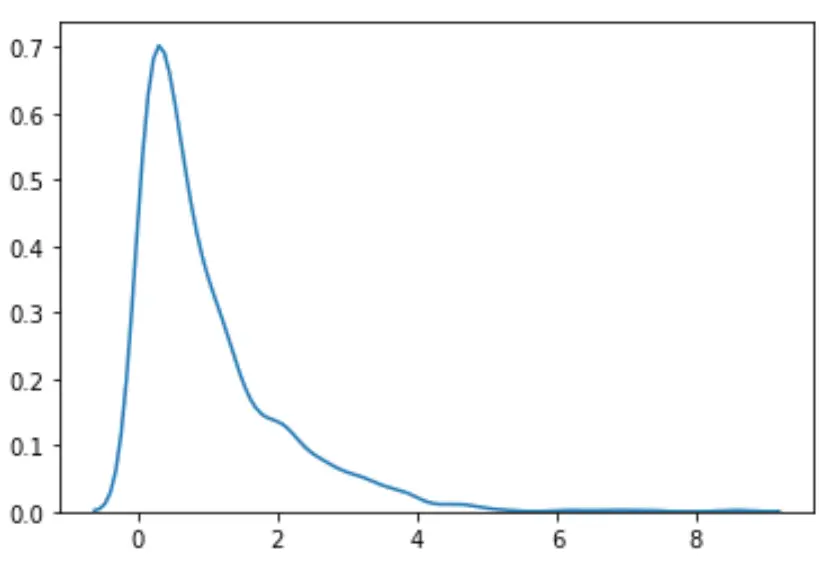
Podemos ver que a distribuição não parece normal.

Podemos usar a função boxcox() para encontrar um valor ideal de lambda que produza uma distribuição mais normal:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

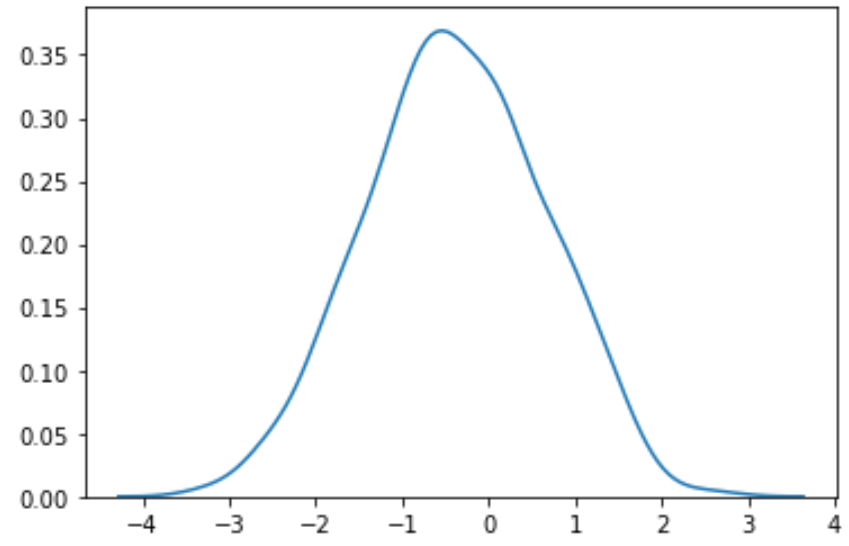
Podemos ver que os dados transformados seguem uma distribuição muito mais normal.

Também podemos encontrar o valor lambda exato usado para realizar a transformação Box-Cox:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

O lambda ideal foi encontrado em torno de 0,242 .

Assim, cada valor de dados foi transformado usando a seguinte equação:

Novo = (antigo ^0,242 – 1) / 0,242

Podemos confirmar isso observando os valores dos dados originais versus os dados transformados:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

O primeiro valor no conjunto de dados original foi 0,79587 . Então, aplicamos a seguinte fórmula para transformar esse valor:

Novo = (0,79587 ^0,242 – 1) / 0,242 = -0,222

Podemos confirmar que o primeiro valor no conjunto de dados transformado é de fato -0,222 .

Recursos adicionais

Como criar e interpretar um gráfico QQ em Python
Como realizar um teste de normalidade Shapiro-Wilk em Python