O que é restrição de escopo?

Muitas vezes, nas estatísticas, procuramos medir a correlação entre duas variáveis. Isso nos ajuda a entender o seguinte:

• A direção da relação entre duas variáveis. À medida que uma variável aumenta, a outra variável tende a aumentar ou diminuir?
• A força da relação entre duas variáveis. Quanto muda o valor das duas variáveis?

Infelizmente, um problema que pode surgir ao medir a correlação entre duas variáveis é chamado de restrição de intervalo . Isso ocorre quando a faixa de valores medidos para uma das variáveis é restrita por algum motivo.

Por exemplo, suponha que queiramos medir a correlação entre as horas de estudo e as notas dos exames dos alunos de uma determinada escola.

Se coletarmos dados sobre essas duas variáveis para todos os 1.000 alunos da escola, poderemos descobrir que a correlação entre as horas estudadas e as notas nos exames é de 0,73 .

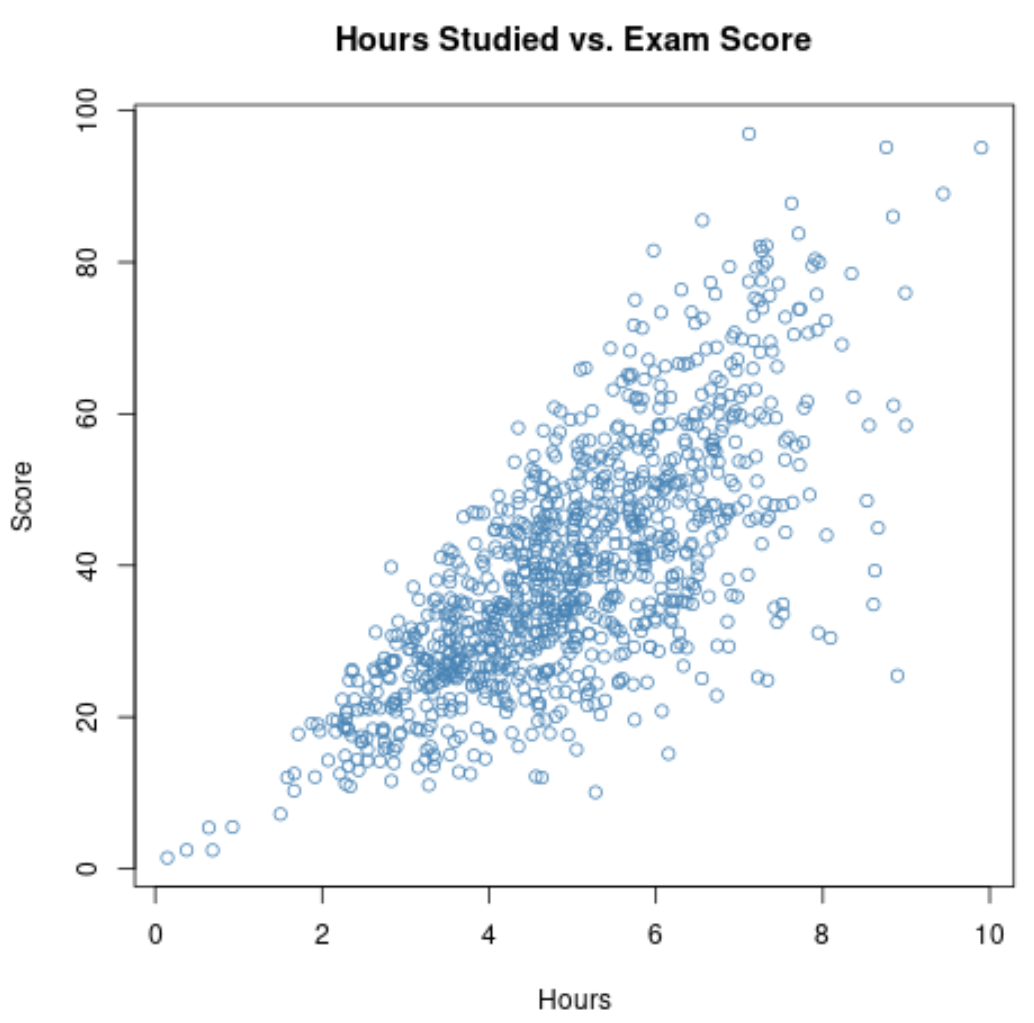
Esta correlação é bastante elevada, indicando uma forte relação positiva entre as duas variáveis. À medida que os alunos estudam mais, eles tendem a ter melhor desempenho nos exames.

No entanto, vamos supor que coletamos dados apenas sobre alunos de cursos especiais. Pode ser que todos esses alunos tenham estudado pelo menos 6 horas.

Portanto, se calcularmos a correlação entre as horas estudadas e as notas dos exames desses alunos, usaríamos uma faixa estreita para as variáveis horas estudadas .

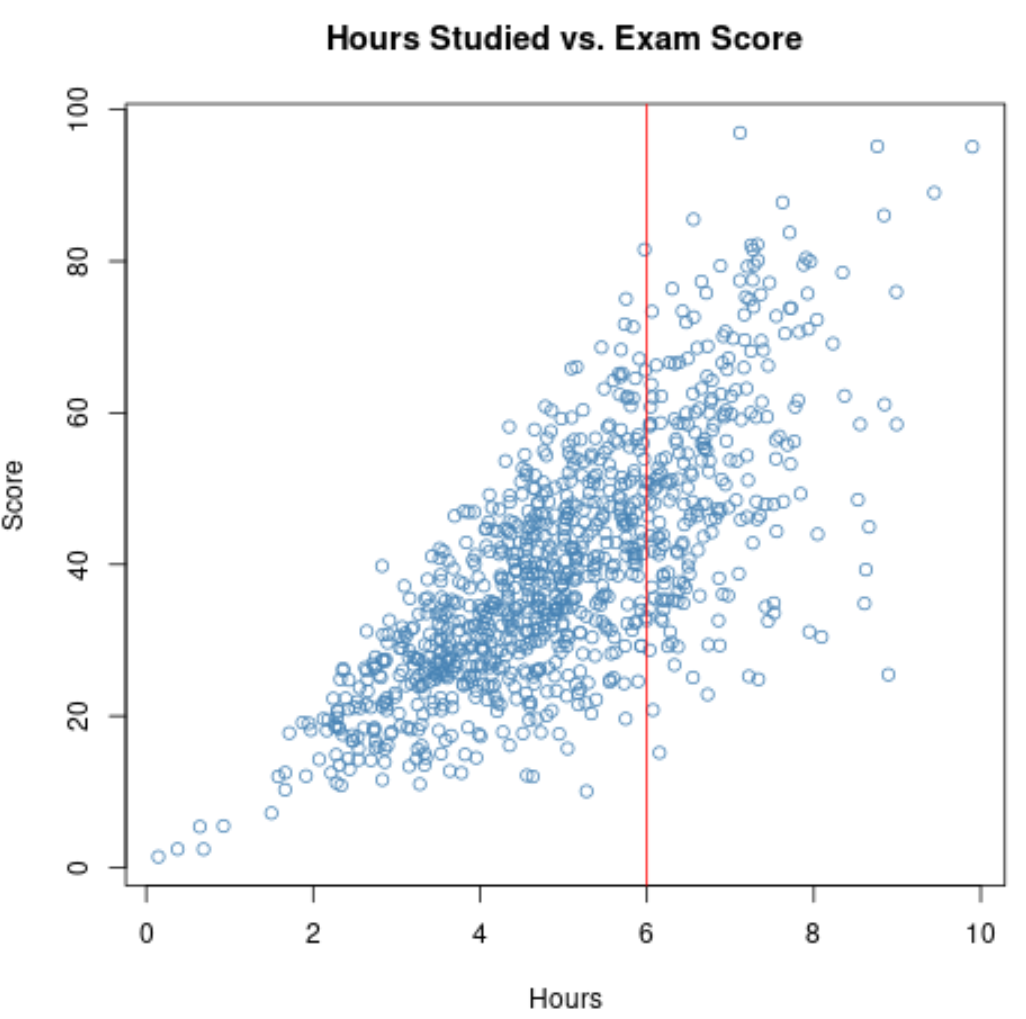
Se ampliarmos o gráfico de dispersão para o intervalo em que as horas são maiores que 6, o gráfico ficará assim:

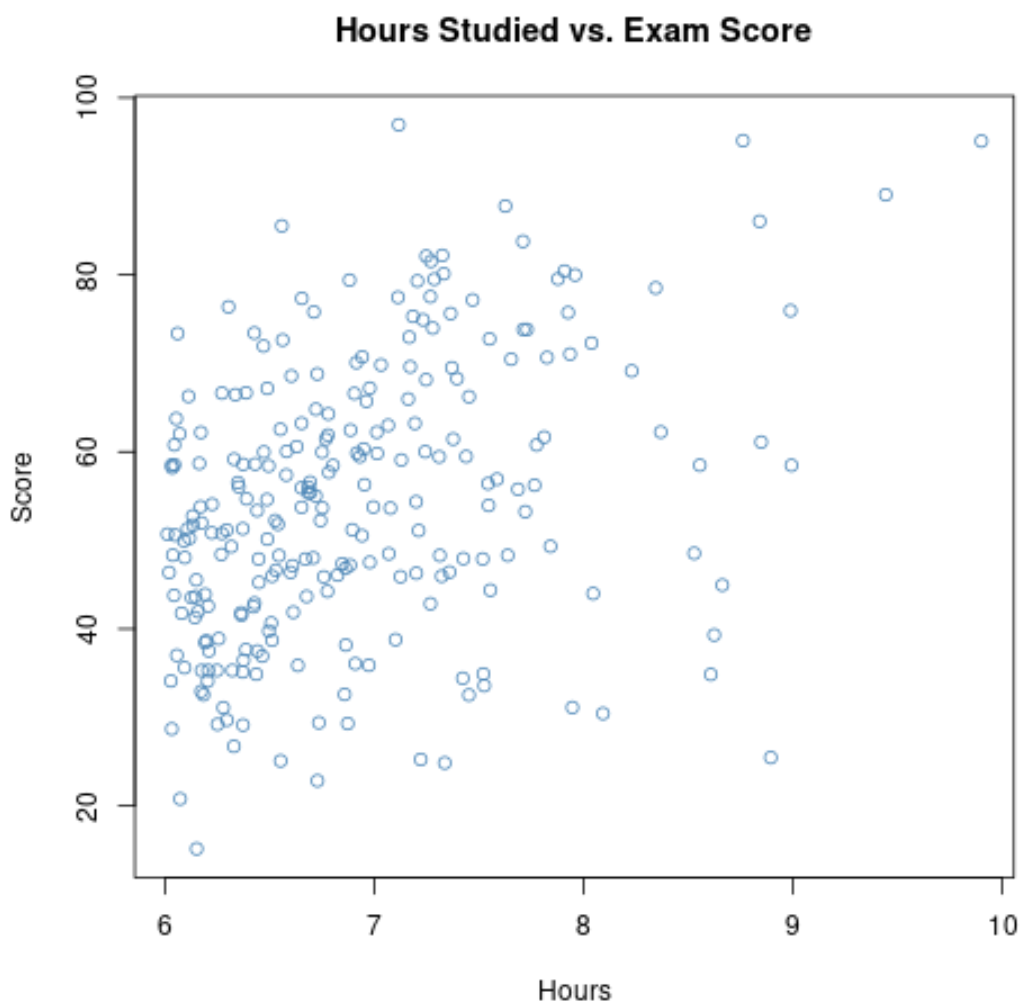
A correlação entre as duas variáveis neste gráfico é de 0,37 , o que é significativamente inferior a 0,73 .

Assim, se coletarmos apenas dados sobre horas estudadas e notas em exames para alunos de cursos com distinção, poderíamos supor que existe uma relação fraca entre horas estudadas e notas em exames.

Contudo, este resultado seria enganoso porque utilizamos um intervalo restrito para uma das variáveis.

Exemplos do mundo real de alcance restrito

O problema de uma faixa restrita pode surgir na prática em muitos estudos de pesquisa diferentes. aqui estão alguns exemplos:

1. Estudos sobre atletas de alto rendimento . Os investigadores podem estar interessados em estudar se um determinado programa de treino produz mais massa muscular do que um determinado programa padrão.

Se os pesquisadores coletarem dados apenas sobre atletas de elite, é provável que todos esses atletas já tenham massa muscular elevada. Haverá, portanto, uma gama estreita de valores disponíveis para calcular a correlação entre o programa de treino e a massa muscular produzida.

2. Estudos de estudantes de alto desempenho. Os pesquisadores podem querer estudar se um determinado programa de tutoria tem ou não um efeito positivo nas notas. Por natureza, os alunos ansiosos por melhorar suas notas e participar do programa de tutoria já podem ser alunos de alto desempenho.

Portanto, pode não haver muito espaço para melhorias nas notas desses alunos. Quando os investigadores calculam a correlação entre as horas passadas no programa de tutoria e o aumento de notas resultante, a verdadeira correlação pode ser subestimada porque o espaço para melhoria de notas foi restrito.

Como contabilizar intervalos restritos

Uma forma popular de contabilizar faixas restritas é conhecida como Caso Thorndike 2 , uma fórmula desenvolvida pelo psicometrista Robert L. Thorndike.

Esta fórmula fornece uma estimativa da verdadeira correlação entre duas variáveis e utiliza o seguinte cálculo:

Correlação verdadeira = √(1-(SD ² _{y restrito} -SD ² _{y irrestrito} )) * (1-r ² _restrito )

Ouro:

• SD ² _{y restrito} : O desvio padrão quadrático dos dados disponíveis na variável resposta y.
• SD _irrestrito ² anos: O desvio padrão quadrático conhecido da variável de resposta para a população.
• r ² _restrito : A correlação quadrática nos dados restritos disponíveis.

Esta fórmula demonstrou ser eficaz na produção de estimativas imparciais da verdadeira correlação entre duas variáveis quando uma das variáveis sofre de um intervalo restrito.

Observe que para usar esta fórmula, você deve ter uma estimativa do verdadeiro desvio padrão da população para a variável de resposta.