Como calcular o desvio padrão relativo no excel

O desvio padrão relativo é uma medida do desvio padrão amostral da média amostral para um determinado conjunto de dados.

É calculado da seguinte forma:

Desvio padrão relativo = s/ x * 100%

Ouro:

• s: desvio padrão da amostra
• x : médias amostrais

Essa métrica nos dá uma ideia de quão próximas as observações estão agrupadas em torno da média.

Por exemplo, suponha que o desvio padrão de um conjunto de dados seja 4. Se a média for 400, então o desvio padrão relativo será 4/400 * 100% = 1%. Isso significa que as observações estão fortemente agrupadas em torno da média.

No entanto, um conjunto de dados com desvio padrão de 40 e média de 400 terá um desvio padrão relativo de 10%. Isto significa que as observações estão muito mais distribuídas em torno da média em comparação com o conjunto de dados anterior.

Este tutorial fornece um exemplo de cálculo do desvio padrão relativo no Excel.

Exemplo: desvio padrão relativo no Excel

Suponha que temos o seguinte conjunto de dados no Excel:

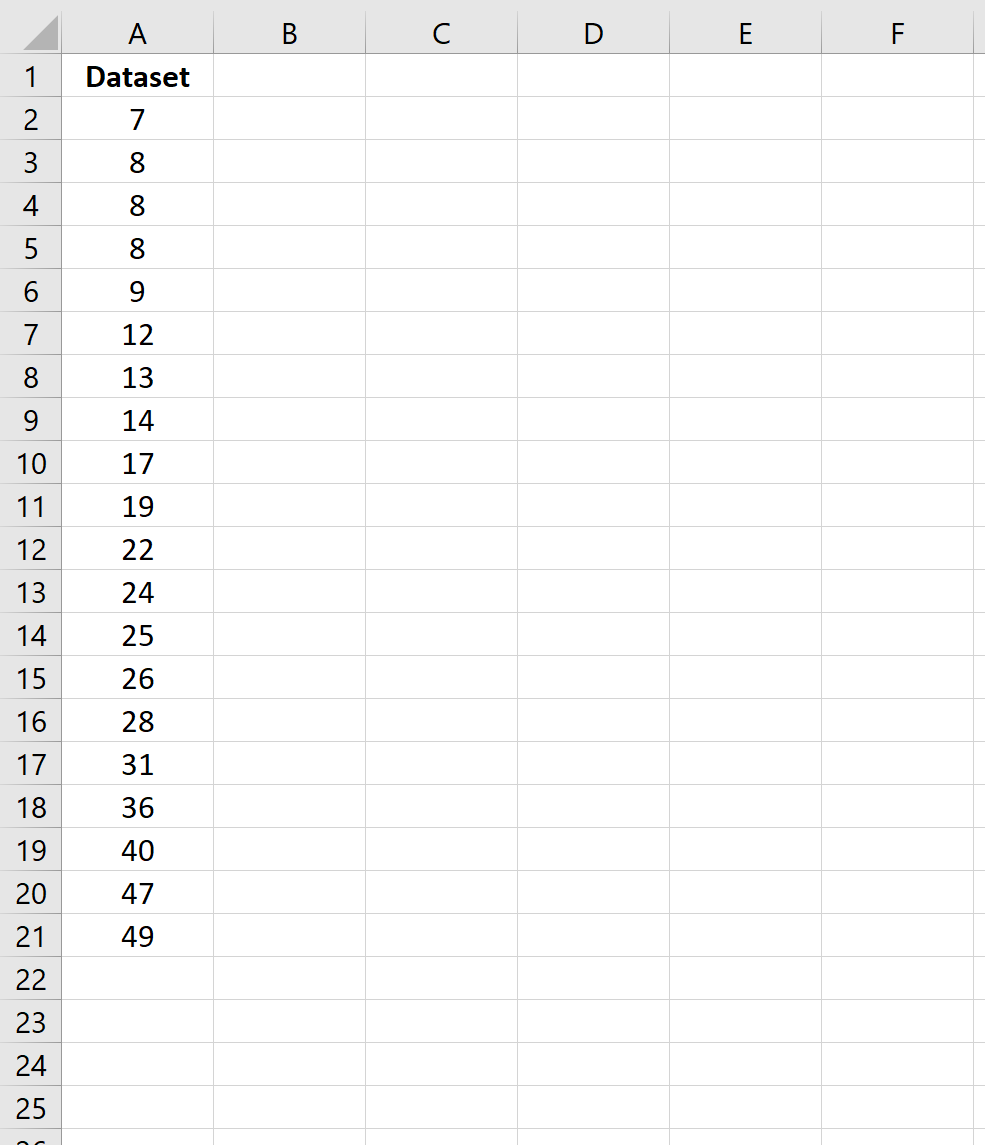
As fórmulas a seguir mostram como calcular a média amostral, o desvio padrão amostral e o desvio padrão relativo amostral do conjunto de dados:

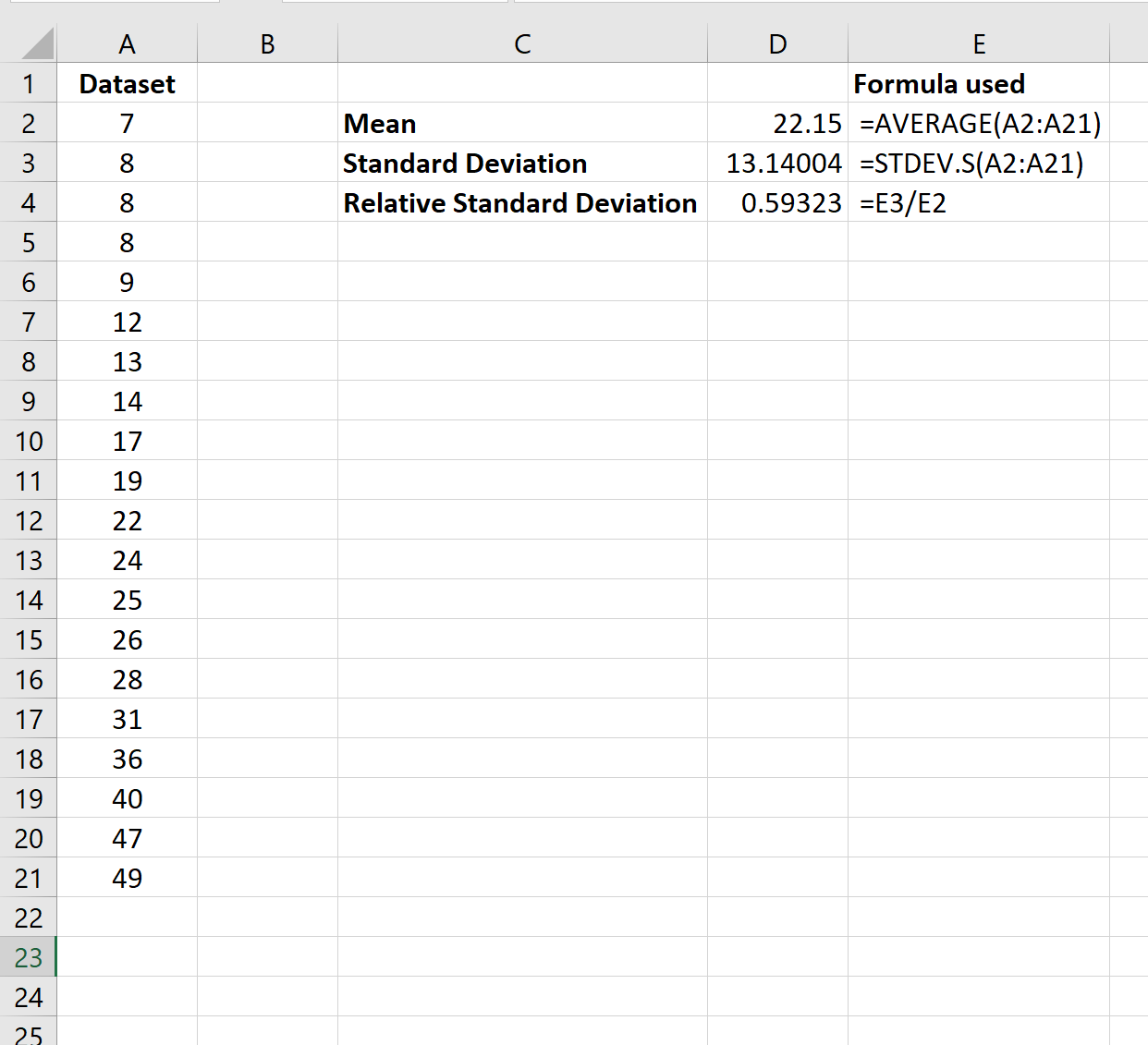
O desvio padrão relativo acaba sendo 0,59 .

Isso nos diz que o desvio padrão do conjunto de dados é 59% do tamanho da média do conjunto de dados. Este número é bastante grande, indicando que os valores estão bastante espalhados em torno da média amostral.

Se tivermos vários conjuntos de dados, podemos usar a mesma fórmula para calcular o desvio padrão relativo (RSD) para cada conjunto de dados e comparar os RSDs entre os conjuntos de dados:

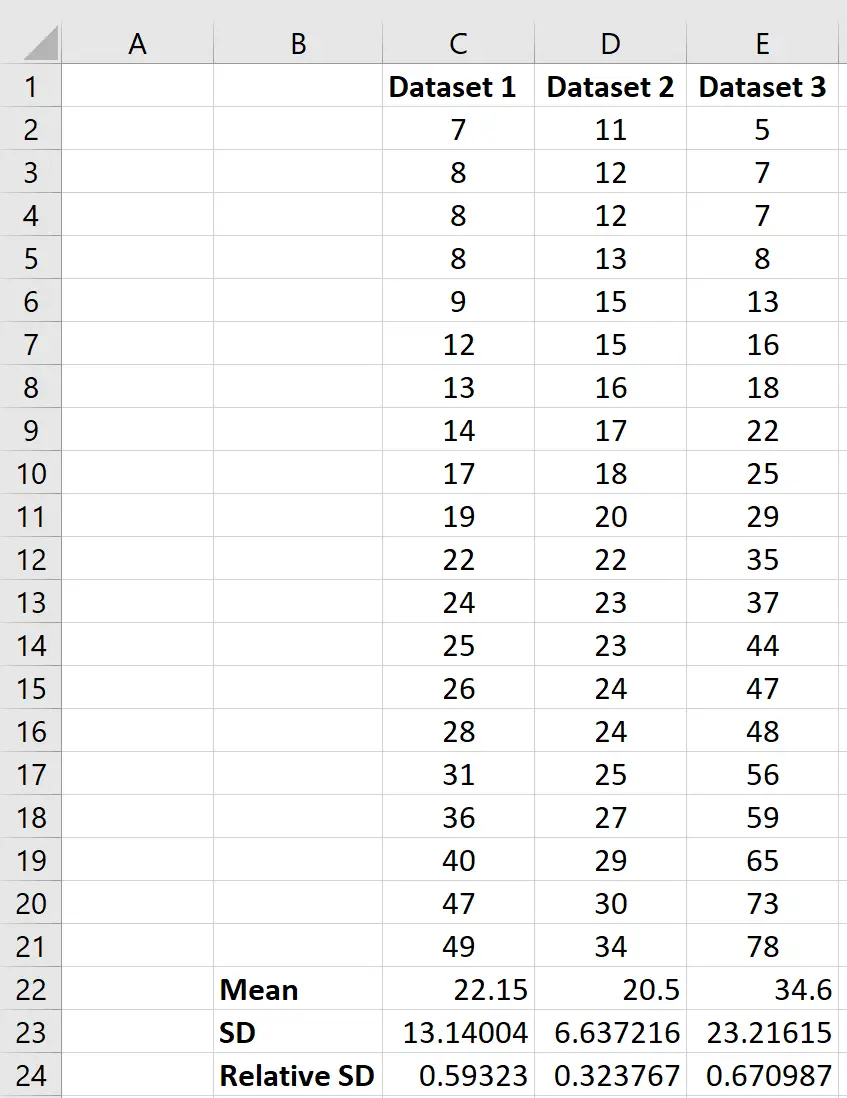
Podemos ver que o conjunto de dados 3 tem o maior desvio padrão relativo, indicando que os valores neste conjunto de dados são os mais dispersos da média do conjunto de dados.

Por outro lado, podemos ver que o conjunto de dados 2 tem o menor desvio padrão relativo, indicando que os valores neste conjunto de dados são os menos dispersos da média deste conjunto de dados específico.

Você pode encontrar mais tutoriais de Excel aqui .