Teste brown-forsythe em r: exemplo passo a passo

Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença significativa entre as médias de três ou mais grupos independentes.

Uma das suposições de uma ANOVA unidirecional é que as variâncias das populações das quais as amostras são extraídas são iguais.

Uma das maneiras mais comuns de testar isso é usar um teste de Brown-Forsythe , que é um teste estatístico que usa as seguintes suposições :

• H ₀ : As variâncias entre as populações são iguais.
• _HA : As diferenças entre as populações não são iguais.

Se o valor p do teste estiver abaixo de um certo nível de significância (por exemplo, α = 0,05), então rejeitamos a hipótese nula e concluímos que as variâncias não são iguais entre diferentes populações.

Este tutorial fornece um exemplo passo a passo de como realizar um teste de Brown-Forsythe em R.

Passo 1: Insira os dados

Suponha que gostaríamos de saber se três programas de treino diferentes levam ou não a diferentes níveis de perda de peso.

Para testar isso, recrutamos 90 pessoas e designamos aleatoriamente 30 para usar cada programa. Em seguida, medimos a perda de peso de cada pessoa após um mês.

O seguinte conjunto de dados contém informações sobre a quantidade de peso perdido com cada programa:

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

Etapa 2: resumir e visualizar os dados

Antes de realizar um teste de Brown-Forsythe, podemos criar box plots para visualizar a variação na perda de peso para cada grupo:

 boxplot(weight_loss ~ program, data = data)

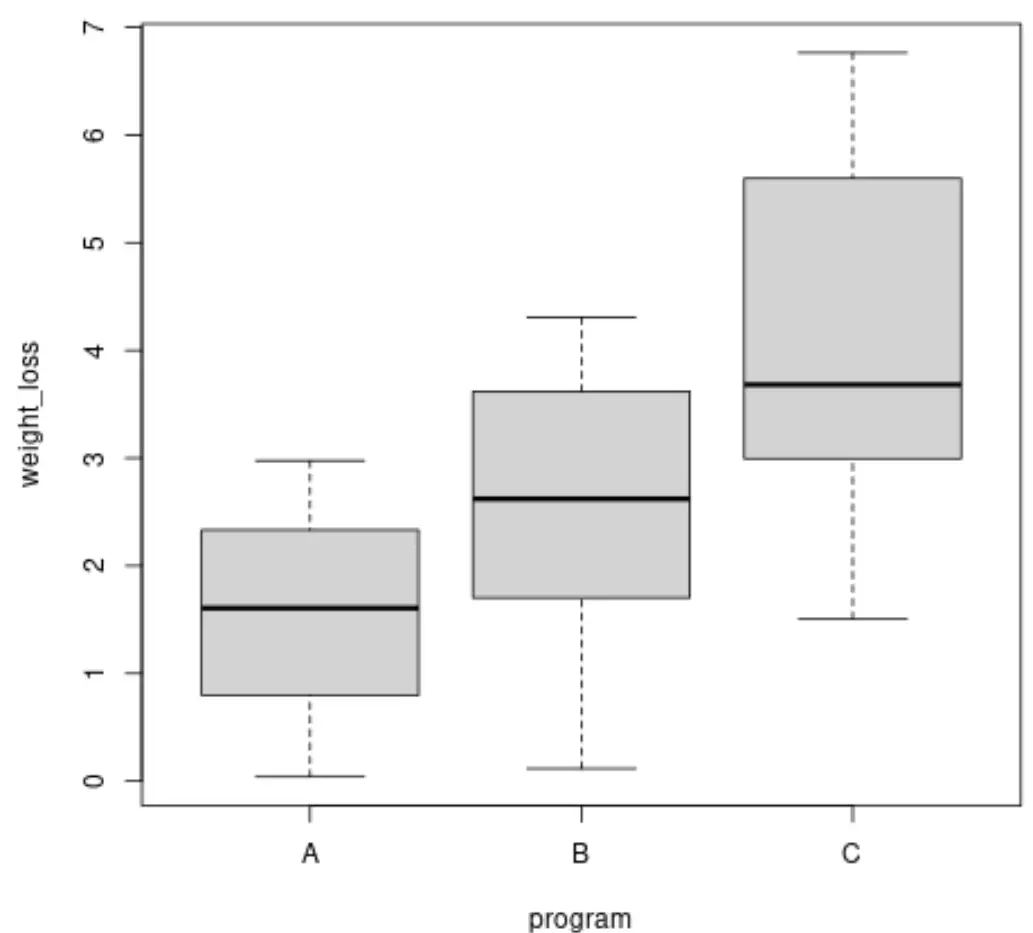
Também podemos calcular a variância da perda de peso em cada grupo:

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

Podemos ver que as variâncias entre os grupos diferem, mas para determinar se essas diferenças são estatisticamente significativas , podemos realizar o teste de Brown-Forsythe.

Etapa 3: execute o teste Brown-Forsythe

Para realizar um teste de Brown-Forsythe em R, podemos usar a função bf.test() do pacote onewaytests :

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

O valor p do teste acaba sendo inferior a 0,000 e, como o resultado indica, as diferenças nas variâncias entre os três grupos são estatisticamente significativas.

Próximos passos

Se você não conseguir rejeitar a hipótese nula do teste de Brown-Forsythe, poderá realizar uma ANOVA unidirecional nos dados.

No entanto, se você rejeitar a hipótese nula, isso significa que a suposição de igualdade de variâncias foi violada. Neste caso, você tem duas opções:

1. Faça uma ANOVA unidirecional de qualquer maneira.

Acontece que uma ANOVA unidirecional é realmente robusta para variâncias desiguais, desde que a maior variância não seja maior que 4 vezes a menor variância.

Na etapa 2 do exemplo acima, descobrimos que a menor variância foi 0,819 e a maior variância foi 2,46. Portanto, a razão entre a maior e a menor variância é 2,46 / 0,819 = 3,003 .

Como esse valor é menor que 4, poderíamos simplesmente fazer a ANOVA unidirecional.

2. Faça um teste de Kruskal-Wallis

Se a razão entre a maior variância e a menor variância for maior que 4, pode-se optar por realizar um teste de Kruskal-Wallis . Isto é considerado o equivalente não paramétrico da ANOVA unidirecional.

Você pode encontrar um exemplo passo a passo de um teste de Kruskal-Wallis em R aqui .