Digitando
Este artigo explica o que significa caracterizar uma distribuição nas estatísticas. Assim, você encontrará a definição de tipificação, um exemplo de tipificação de uma variável e, além disso, poderá praticar com um exercício resolvido passo a passo.
O que é digitação?
Em estatística, a normalização é um processo no qual uma transformação linear é aplicada a uma distribuição tal que sua média e desvio padrão sejam iguais a zero e um, respectivamente.
Mais precisamente, a digitação envolve subtrair a média da variável aleatória e depois dividi-la pelo desvio padrão.
A digitação também pode ser chamada de normalização ou padronização.
Fórmula de entrada
Para classificar uma variável, você deve subtrair sua média e depois dividi-la pelo seu desvio padrão. A fórmula para inserir uma variável é, portanto, a seguinte:
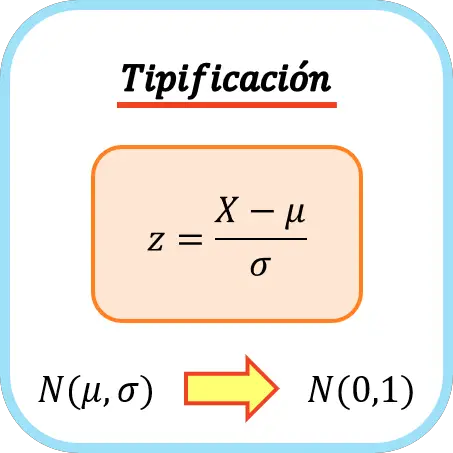
Ouro
![]()
é a média da variável
![]()
E
![]()
seu desvio padrão (ou desvio padrão).
Portanto, a entrada é na verdade uma mudança de variável, uma vez que uma transformação linear é aplicada à variável.
Entrada de exemplo
Considerando a definição de tipificação e sua fórmula, segue abaixo um exemplo concreto para a compreensão completa do conceito.
- Uma variável aleatória contínua segue uma distribuição normal com média 45 e desvio padrão 10, qual a probabilidade de obter um valor menor ou igual a 60?
![]()
Para encontrar a probabilidade de uma distribuição normal precisamos usar sua tabela de características, mas para isso precisamos primeiro realizar o processo de digitação. Então subtraímos a média e dividimos pelo desvio padrão para o valor da probabilidade:
![]()
Depois de padronizarmos, passamos para a tabela de probabilidade de distribuição normal para ver a que probabilidade corresponde o valor de 1,5:

Como pode ser observado na tabela de tipificação da distribuição normal, o valor calculado na etapa anterior corresponde à seguinte probabilidade:
![]()
A probabilidade de obter um valor igual ou inferior a 60 é, portanto, de 93,32%.
Exercício de digitação resolvido
Calcule as seguintes probabilidades de uma distribuição normal cuja média e desvio padrão são 120 e 50, respectivamente.
![]()
- A probabilidade de obter um valor menor ou igual a 208.
- A probabilidade de obter um valor superior a 137.
Em ambas as seções do problema, precisamos digitar a distribuição normal para calcular as probabilidades.
Começamos calculando a tipagem de probabilidade de um valor menor ou equivalente a 208:
![]()
E agora vamos dar uma olhada na tabela acima a que probabilidade corresponde o valor 1,76:
![]()
Em segundo lugar, calcularemos a probabilidade de obter um valor superior a 137. Da mesma forma, começaremos digitando a variável:
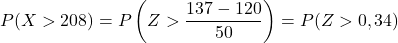 No entanto, a tabela anexa apresenta apenas as probabilidades cumulativas mais baixas, portanto, para utilizar a tabela devemos primeiro transformar a probabilidade:
No entanto, a tabela anexa apresenta apenas as probabilidades cumulativas mais baixas, portanto, para utilizar a tabela devemos primeiro transformar a probabilidade:
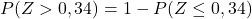 E, por fim, anotaremos na tabela anexa a probabilidade correspondente ao valor calculado de Z:
E, por fim, anotaremos na tabela anexa a probabilidade correspondente ao valor calculado de Z:
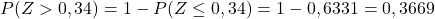
Qual é o sentido de digitar?
Para finalizar a compreensão do significado da tipificação, veremos para que ela serve e quando uma variável deve ser digitada.
Principalmente, a padronização é usada para comparar os valores das distribuições com diferentes médias e variâncias. Da mesma forma, a padronização também é usada para calcular uma probabilidade.
Ao padronizar dois valores de distribuições com características diferentes, podemos ver qual valor é maior ou menor em relação a toda a distribuição. Ou seja, aplicando o processo de tipificação, podemos perceber qual valor está mais próximo ou mais distante da média de sua distribuição.
Adicionalmente, conforme explicado acima, a tipificação também permite o cálculo de probabilidades, uma vez que geralmente as tabelas de probabilidades são baseadas em uma distribuição tipificada.