Diagrama de caule e folha
Este artigo explica o que são diagramas de caule e folha nas estatísticas e para que são usados. Você descobrirá, portanto, como construir um diagrama caule-folha, exercícios resolvidos para este tipo de gráfico estatístico e, por fim, quais são as vantagens e desvantagens do diagrama caule-folha.
Qual é o diagrama caule-folha?
O diagrama de caule e folha é um tipo de diagrama estatístico no qual um conjunto de dados quantitativos é representado.
Em um diagrama caule-folha, cada ponto de dados é separado pela folha , que é seu último dígito, e pelo caule , que são os dígitos restantes. Assim, num diagrama caule-folha, cada folha é colocada na linha do seu caule correspondente.
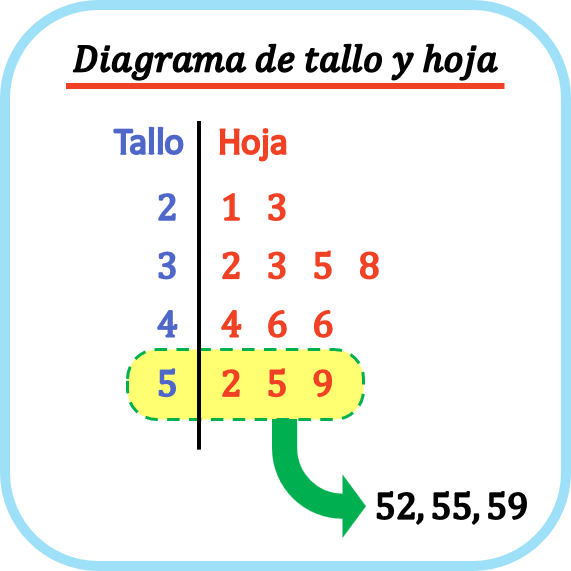
Dessa forma, os gráficos de caule e folhas ajudam a representar graficamente um conjunto de dados estatísticos e também a visualizar a forma da distribuição.
O diagrama de caule e folha também é conhecido como diagrama de caule e folha , nome que vem do inglês.
A plotagem de caule e folhas é muito semelhante ao histograma , embora este outro tipo de gráfico estatístico seja usado para amostras maiores.
Como fazer um diagrama de caule e folha
Para criar um diagrama de caule e folha, siga estas etapas:
- Classifique os dados do menor para o maior.
- Se necessário, arredonde os números até que tenham o número de dígitos desejado.
- Decida em qual figura será feito o corte entre o caule e a folha, ou seja, determine a quantidade de figuras que as folhas terão. Normalmente, a planilha é projetada para conter apenas o último dígito de cada item de dados.
- Represente cada dado no diagrama de caule e folha. Os caules são colocados na coluna da esquerda em ordem crescente, enquanto as folhas são colocadas na coluna da direita na altura do caule correspondente e também em ordem crescente.
Exemplo de gráfico de caule e folha
Para que você possa ver como criar um diagrama de caule e folha, resolvemos dois exemplos abaixo: um sem decimais e outro com decimais.
Exemplo 1
- Trace a seguinte série de dados em um diagrama de caule e folha:

Neste caso os dados já estão ordenados e arredondados, não sendo necessário realizar estes dois passos. Assim, como os números possuem dois algarismos, eles serão representados de forma que os tempos sejam o radical e os uns sejam as folhas do gráfico.
Representaremos primeiro a haste do diagrama. O tempo verbal dos dados vai até 9, então fazemos uma linha para cada dez:

E a seguir representamos as folhas, para isso colocamos a unidade de cada dado em sua linha correspondente. Por exemplo, o número 57 irá para a raiz de 5 e na coluna da direita adicionaremos um 7.
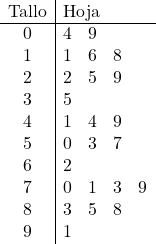
E desta forma, todos os dados amostrais foram representados em um gráfico de caule e folhas.
Exemplo 2
- Compare as duas amostras de dados a seguir com decimais usando um gráfico de caule e folhas.


Como você verá neste exercício, um único gráfico de caule e folhas pode ser usado para representar duas amostras estatísticas. Portanto, representaremos ambos os conjuntos de dados no mesmo gráfico de caule e folhas: um à esquerda e outro à direita. Esse tipo de gráfico é chamado de gráfico de caule e folhas de caule duplo .
Neste caso, tomaremos toda a parte dos números como raiz do diagrama e, por outro lado, os decimais serão as folhas do diagrama. Portanto, construímos o layout do caule e da folha colocando todas as partes inteiras:
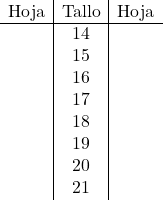
E agora colocamos a planilha de cada dado no caule que lhe corresponde:
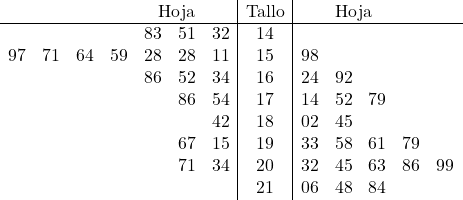
Ao representar os dados graficamente, podemos compará-los facilmente. Especificamente, vemos que os dados da amostra à direita são um pouco maiores que os da amostra à esquerda, portanto sua média também será maior. Assim, dependendo do objetivo do estudo estatístico, teremos interesse em escolher esta ou aquela amostra.
Tenha em mente que você não só precisa saber como construir um gráfico de barras e lâminas, mas também como interpretá-lo.
Vantagens e desvantagens da parcela de caule e folha
Devido às características da parcela de caule e folhas, estes tipos de parcelas apresentam as seguintes vantagens e desvantagens:
Vantagem:
- Traçar os caules e folhas permite ver a forma de uma distribuição.
- Duas distribuições podem ser comparadas usando o gráfico de caule e folhas de caule duplo.
- Ele permite identificar rapidamente valores discrepantes em um conjunto de dados.
- Você pode determinar o modo da série de dados a olho nu.
Desvantagens:
- O diagrama de caule e folha está sendo cada vez menos usado porque o software de computador pode criar rapidamente um gráfico mais complexo.
- O tamanho da amostra a representar é limitado, geralmente entre 15 e 150 pontos de dados.
- Apenas dados quantitativos podem ser representados.