Como plotar resultados de regressão linear múltipla em r

Quando realizamos regressão linear simples em R, é fácil visualizar a linha de regressão ajustada porque estamos trabalhando apenas com uma única variável preditora e uma única variável de resposta .

Por exemplo, o código a seguir mostra como ajustar um modelo de regressão linear simples a um conjunto de dados e representar graficamente os resultados:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

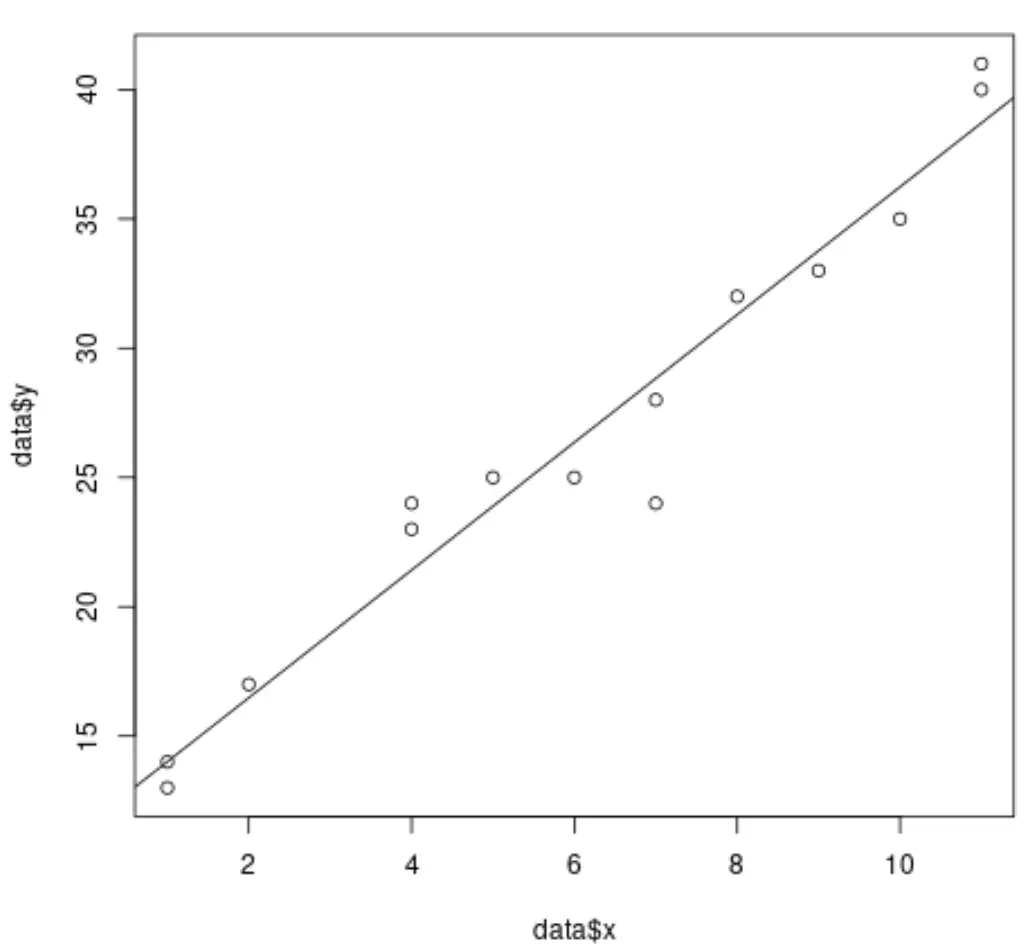
No entanto, quando realizamos regressão linear múltipla, torna-se difícil visualizar os resultados porque existem múltiplas variáveis preditoras e não podemos simplesmente traçar uma linha de regressão em um gráfico 2D.

Em vez disso, podemos usar gráficos de variáveis adicionadas (às vezes chamados de “gráficos de regressão parcial”), que são gráficos individuais que exibem o relacionamento entre a variável de resposta e uma variável preditora, enquanto controlam a presença de outras variáveis preditoras no modelo .

O exemplo a seguir mostra como realizar regressão linear múltipla em R e visualizar os resultados usando gráficos de variáveis anexados.

Exemplo: plotando resultados de regressão linear múltipla em R

Suponha que ajustamos o seguinte modelo de regressão linear múltipla a um conjunto de dados em R usando o conjunto de dados mtcars integrado:

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

A partir dos resultados, podemos ver que o valor p para cada um dos coeficientes é inferior a 0,1. Para simplificar, assumiremos que cada uma das variáveis preditoras é significativa e deve ser incluída no modelo.

Para produzir gráficos de variáveis anexadas, podemos usar a função avPlots() do pacote car :

 #load car package
library(car)

#produce added variable plots
avPlots(model)

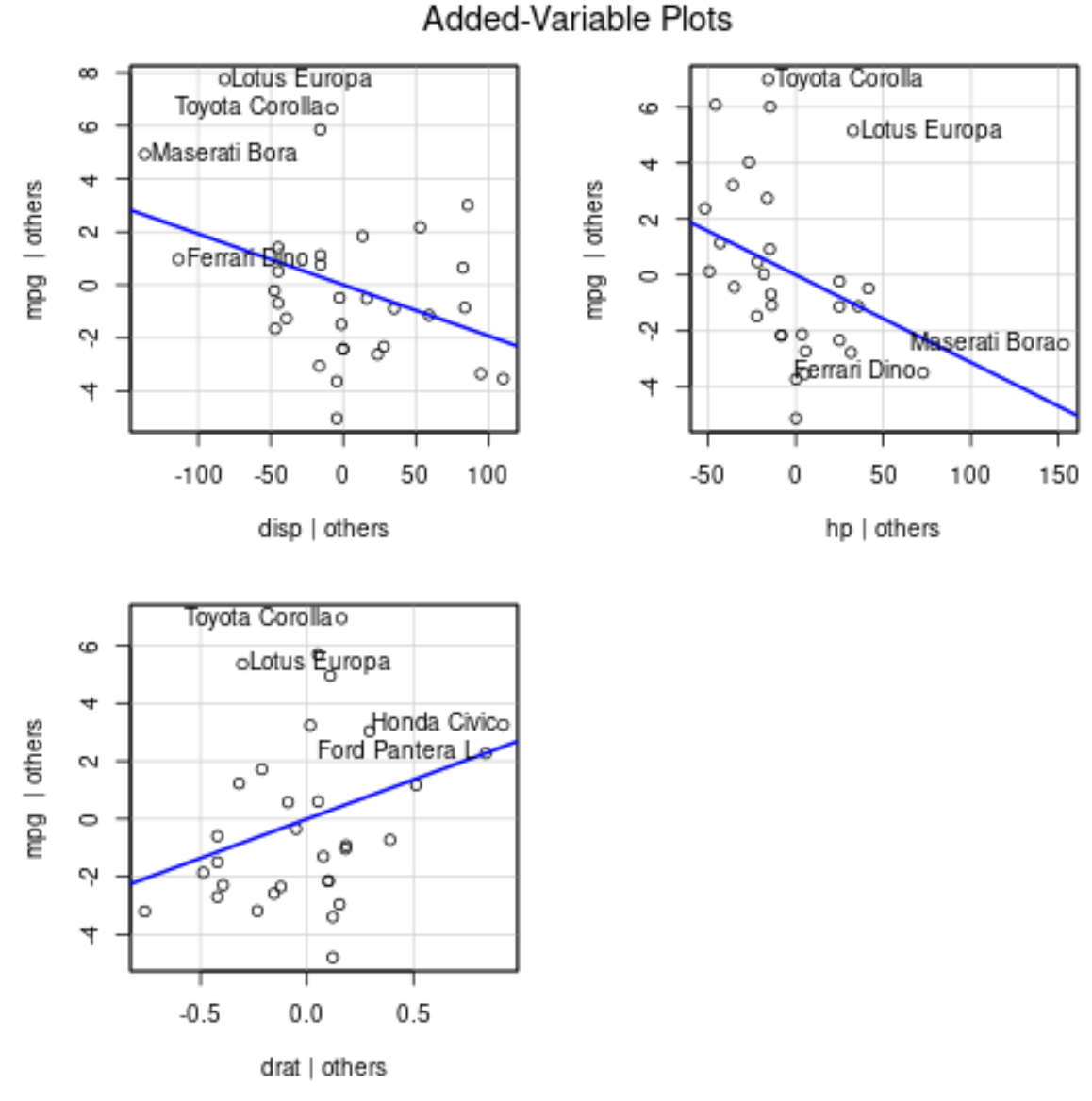
Veja como interpretar cada enredo:

• O eixo x exibe uma única variável preditora e o eixo y exibe a variável de resposta.
• A linha azul mostra a associação entre a variável preditora e a variável resposta, enquanto mantém constante o valor de todas as outras variáveis preditoras .
• Os pontos rotulados em cada gráfico representam as 2 observações com os maiores resíduos e as 2 observações com a maior alavancagem parcial.

Observe que o ângulo da reta em cada gráfico corresponde ao sinal do coeficiente da equação de regressão estimada.

Por exemplo, aqui estão os coeficientes estimados para cada variável preditora no modelo:

• exibição: -0,019232
• canal: -0,031229
• data: 2.714975

Observe que o ângulo da linha é positivo no gráfico da variável adicionada para drat enquanto é negativo para disp e hp , o que corresponde aos sinais de seus coeficientes estimados:

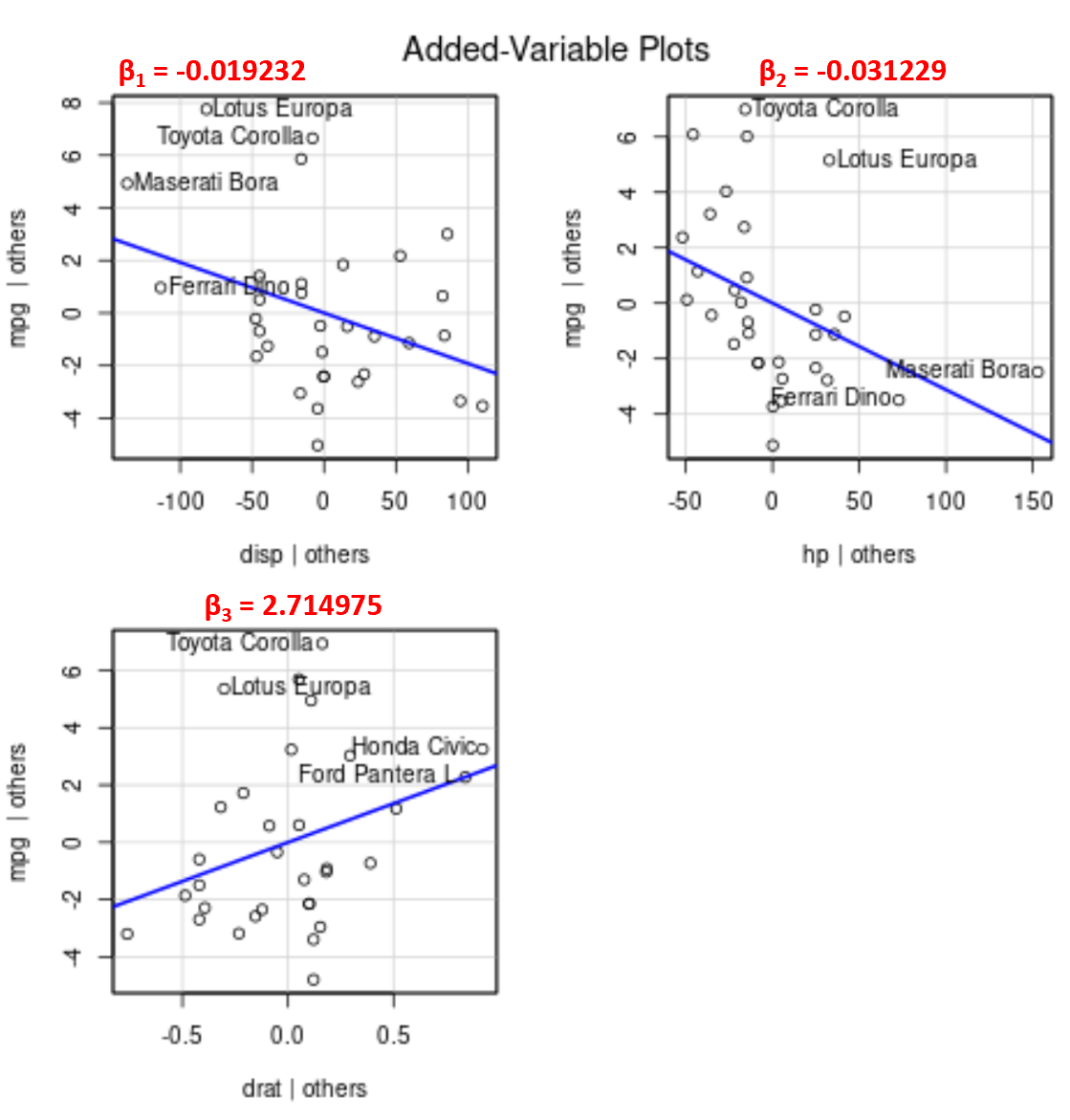
Embora não possamos traçar uma única linha de regressão ajustada em um gráfico 2D, uma vez que temos múltiplas variáveis preditoras, esses gráficos de variáveis adicionados nos permitem observar a relação entre cada variável preditora individual e a variável de resposta, mantendo constantes as outras variáveis preditivas.