O que é uma função de massa de probabilidade (pmf) em estatísticas?

Uma função de massa de probabilidade , frequentemente abreviada como PMF , nos diz a probabilidade de uma variável aleatória discreta assumir um determinado valor.

Por exemplo, suponha que lançamos um dado uma vez. Se deixarmos x denotar o número em que o dado cai, então a probabilidade de x ser igual a valores diferentes pode ser descrita da seguinte forma:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Há uma chance igual de que os dados caiam em qualquer número entre 1 e 6.

Aqui está como escreveríamos essas probabilidades como uma função de massa de probabilidade:

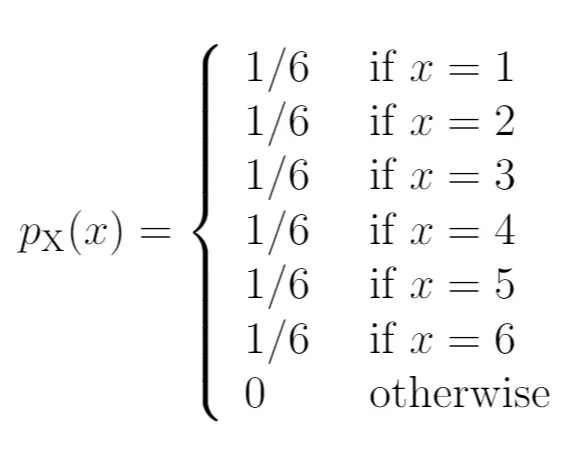
O lado esquerdo do diagrama mostra a probabilidade associada aos resultados do lado direito:

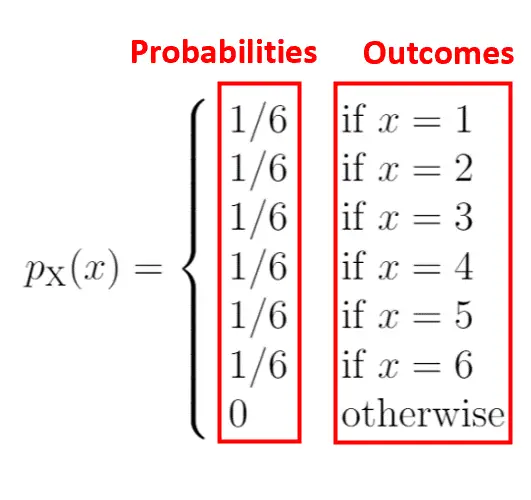
Uma característica de uma função de massa de probabilidade é que todas as probabilidades devem somar 1. Você notará que este PMF satisfaz esta condição:

Soma das probabilidades = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

O suporte para uma função de massa de probabilidade refere-se ao conjunto de valores que a variável aleatória discreta pode assumir. Neste exemplo, o suporte seria {1, 2, 3, 4, 5, 6} já que o valor do dado pode assumir qualquer um desses valores.

Fora do suporte, o valor PMF é zero. Por exemplo, a probabilidade de o dado cair em “0” ou “7” ou “8” é zero, uma vez que nenhum desses números está incluído entre colchetes.

Funções de massa de probabilidade na prática

Os dois exemplos mais comuns de funções de massa de probabilidade na prática dizem respeito à distribuição binomial e à distribuição de Poisson .

Distribuição binomial

Se uma variável aleatória X segue uma distribuição binomial, então a probabilidade de X = k sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Ouro:

• n: número de tentativas
• k: número de sucessos
• p: probabilidade de sucesso em uma determinada tentativa
• _n C _k : o número de maneiras de obter k sucessos em n tentativas

Por exemplo, suponhamos que jogamos uma moeda 3 vezes. Podemos usar a fórmula acima para determinar a probabilidade de obter 0, 1, 2 e 3 caras nestes 3 lançamentos:

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Distribuição de peixes

Se uma variável aleatória X segue uma distribuição de Poisson, então a probabilidade de X = k sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = λ ^k * e ^{– λ} / k!

Ouro:

• λ: número médio de sucessos ocorridos durante um intervalo específico
• k: número de sucessos
• e: uma constante igual a aproximadamente 2,71828

Por exemplo, suponha que um determinado hospital tenha uma média de 2 partos por hora. Podemos usar a fórmula acima para determinar a probabilidade de ocorrer 0, 1, 2, 3 nascimentos, etc. em uma determinada hora:

• P(X=0) = 2 ⁰ * e ^{– 2/0} ! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2/1} ! = 0,2707
• P(X=2) = 2 ² * e ^{– 2/2} ! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2/3} ! = 0,1805

Veja um PMF

Freqüentemente visualizamos funções de massa de probabilidade com gráficos de barras.

Por exemplo, o gráfico de barras a seguir mostra as probabilidades associadas ao número de nascimentos por hora para a distribuição de Poisson descrita no exemplo anterior:

Observe que o número de nascimentos pode se estender até o infinito, mas as probabilidades tornam-se tão pequenas depois de 10 que você nem consegue vê-las em um gráfico de barras.

Propriedades de um PMF

Uma função de massa de probabilidade tem as seguintes propriedades:

1. Todas as probabilidades são positivas no suporte. Por exemplo, a probabilidade de um dado cair entre 1 e 6 é positiva, enquanto a probabilidade de todos os outros resultados é zero.

2. Todos os resultados têm uma probabilidade entre 0 e 1. Por exemplo, a probabilidade de um dado cair entre 1 e 6 é 1/6, ou 0,1666666 para cada resultado.

3. A soma de todas as probabilidades deve ser igual a 1. Por exemplo, a soma das probabilidades de um dado cair sobre um determinado número é 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

Recursos adicionais

O que são variáveis aleatórias?
CDF ou PDF: qual a diferença?
Uma introdução à distribuição binomial
Uma introdução à distribuição de Poisson