Como realizar regressão quantílica em python

A regressão linear é um método que podemos usar para compreender a relação entre uma ou mais variáveis preditoras e uma variável de resposta .

Normalmente, quando realizamos regressão linear, queremos estimar o valor médio da variável resposta.

No entanto, poderíamos, em vez disso, usar um método conhecido como regressão quantílica para estimar qualquer valor quantílico ou percentil do valor da resposta, como o percentil 70, o percentil 90, o percentil 98, etc.

Este tutorial fornece um exemplo passo a passo de como usar esta função para realizar regressão quantílica em Python.

Passo 1: Carregue os pacotes necessários

Primeiro, carregaremos os pacotes e funções necessários:

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

Etapa 2: crie os dados

Para este exemplo, criaremos um conjunto de dados contendo as horas estudadas e os resultados dos exames obtidos para 100 alunos de uma universidade:

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

Etapa 3: realizar a regressão quantílica

A seguir, ajustaremos um modelo de regressão quantílica usando horas estudadas como variável preditora e notas em exames como variável resposta.

Usaremos o modelo para prever o percentil 90 esperado das notas dos exames com base no número de horas estudadas:

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

A partir do resultado podemos ver a equação de regressão estimada:

90º percentil da nota do exame = 59,6104 + 2,8495*(horas)

Por exemplo, a pontuação do percentil 90 de todos os alunos que estudam 8 horas deveria ser 82,4:

90º percentil da nota do exame = 59,6104 + 2,8495*(8) = 82,4 .

A saída também exibe os limites de confiança superior e inferior para a interceptação e os tempos da variável preditora.

Etapa 4: visualize os resultados

Também podemos visualizar os resultados da regressão criando um gráfico de dispersão com a equação de regressão quantílica ajustada sobreposta no gráfico:

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

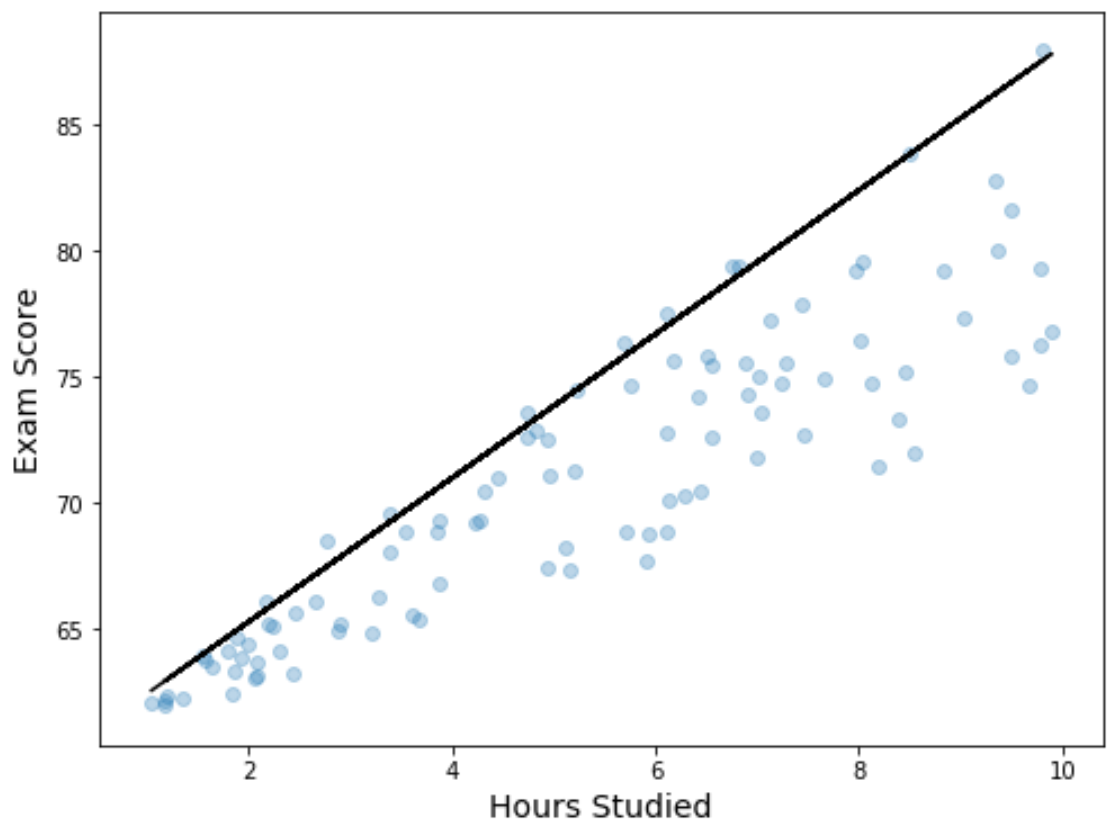
Ao contrário de uma linha de regressão linear simples, observe que esta linha ajustada não representa a “linha de melhor ajuste” para os dados. Em vez disso, passa pelo percentil 90 estimado em cada nível da variável preditora.

Recursos adicionais

Como realizar regressão linear simples em Python
Como realizar regressão quadrática em Python