Eventos mutuamente inclusivos ou mutuamente exclusivos
Dois eventos são mutuamente exclusivos se não puderem ocorrer ao mesmo tempo.
Por exemplo, suponha que o evento A seja o evento em que um dado caia em um número par e o evento B seja o evento em que um dado caia em um número ímpar.
Definiríamos o espaço amostral para eventos da seguinte forma:
- UMA = {2, 4, 6}
- B = {1, 3, 5}
Observe que não há sobreposição entre os dois espaços amostrados. Portanto, os eventos A e B são mutuamente exclusivos porque não podem ocorrer ambos ao mesmo tempo. O número sobre o qual cai um dado não pode ser par e ímpar.
Por outro lado, dois eventos são mutuamente inclusivos se puderem ocorrer ao mesmo tempo.
Por exemplo, seja o evento C o evento em que um dado cai em um número par e seja o evento D o evento em que um dado cai em um número maior que 3.
Definiríamos o espaço amostral para eventos da seguinte forma:
- C = {2, 4, 6}
- d = {4, 5, 6}
Observe que há uma sobreposição entre os dois espaços amostrados. Assim, os eventos C e D são mutuamente inclusivos porque podem ocorrer ao mesmo tempo. É possível que os dados caiam num número par maior que 3.
Probabilidades de eventos
Se dois eventos são mutuamente exclusivos, então a probabilidade de ambos ocorrerem é zero.
Por exemplo, considere os dois espaços de exemplo para os eventos A e B acima:
- UMA = {2, 4, 6}
- B = {1, 3, 5}
Como não há sobreposição nos espaços amostrais, diríamos P(A e B) = 0 .
Mas se dois eventos são mutuamente inclusivos , então a probabilidade de ambos ocorrerem será um número maior que zero.
Por exemplo, considere os dois espaços de exemplo para os eventos C e D anteriormente:
- C = {2, 4, 6}
- d = {4, 5, 6}
Como existem 6 números possíveis em que os dados podem cair e dois desses números (4 e 6) pertencem aos eventos C e D, calcularíamos P(C e D) como 2/6 ou 1/3 .
Veja eventos mutuamente inclusivos e mutuamente exclusivos
Freqüentemente usamos diagramas de Venn para visualizar as probabilidades associadas aos eventos.
Se dois eventos forem mutuamente exclusivos, eles não se sobreporão em um diagrama de Venn:
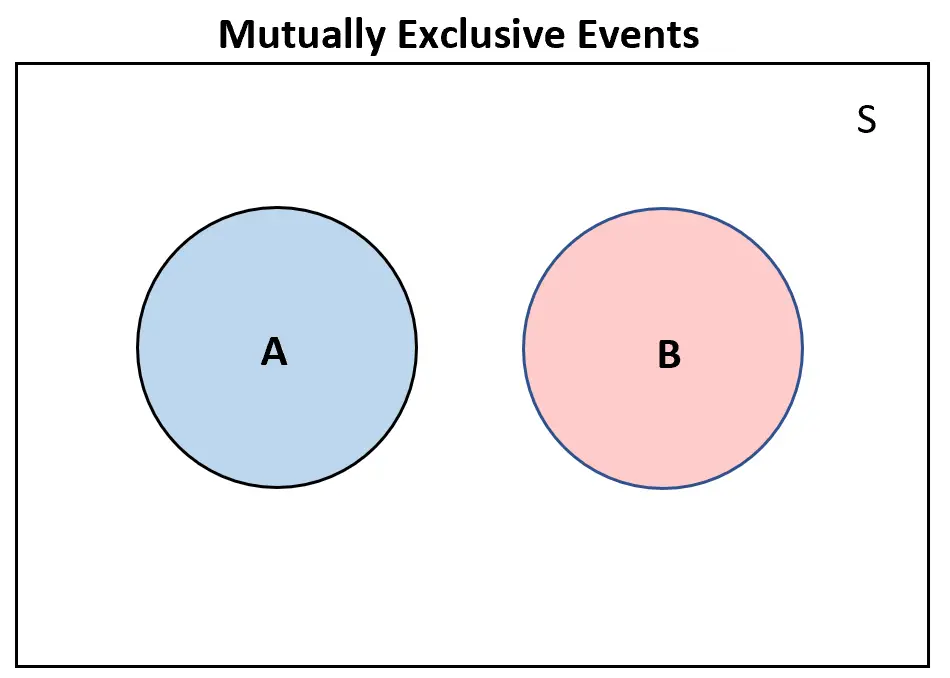
Por outro lado, se dois eventos fossem mutuamente inclusivos , haveria pelo menos alguma sobreposição no diagrama de Venn:
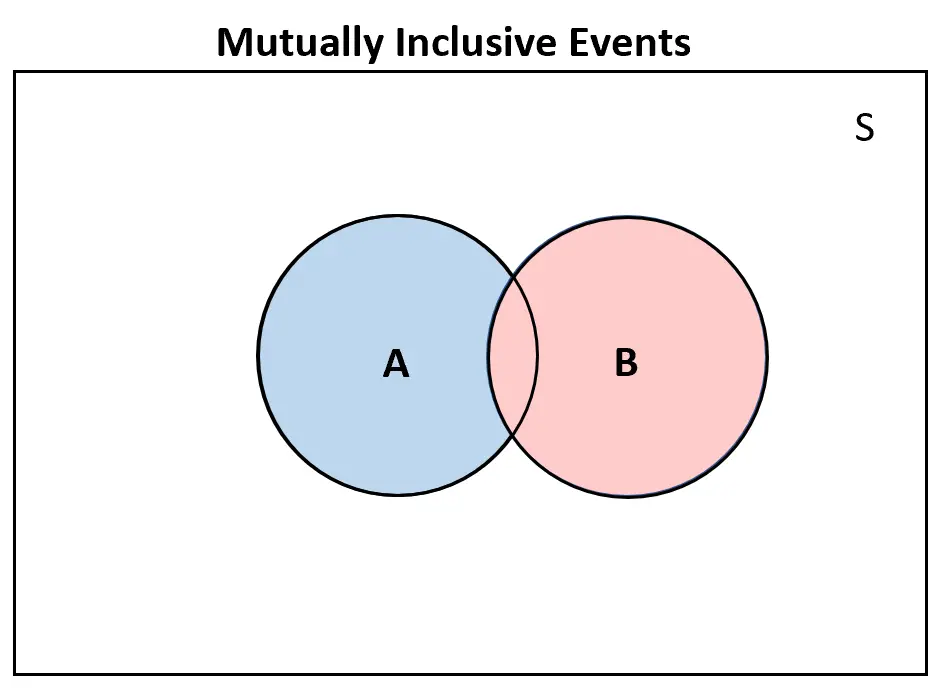
Recursos adicionais
Uma introdução à probabilidade teórica
A regra geral de multiplicação
O que são eventos disjuntos?