O que é uma estimativa pontual nas estatísticas?
Muitas vezes em estatística estamos interessados em medir parâmetros populacionais , ou seja, números que descrevem certas características de uma população inteira.
Dois dos parâmetros populacionais mais comuns são:
1. Média populacional: o valor médio de uma variável em uma população (por exemplo, a altura média dos homens em uma determinada cidade)
2. Proporção populacional: a proporção de uma variável numa população (por exemplo, a proporção de residentes num condado que apoiam uma determinada lei)
Mesmo que queiramos medir estes parâmetros, é geralmente muito caro e demorado recolher dados sobre cada indivíduo numa população.
Em vez disso, pegamos uma amostra aleatória da população e usamos os dados da amostra para estimar o parâmetro populacional.
O número que usamos na amostra para estimar o parâmetro populacional é chamado de estimativa pontual . Esta é a nossa melhor estimativa possível de qual pode ser o verdadeiro parâmetro populacional.
A tabela a seguir mostra a estimativa pontual que usamos para estimar os parâmetros populacionais:
| A medida | Parâmetro populacional | Ponto estimado |
|---|---|---|
| Significar | μ (média da população) | x (média amostral) |
| Proporção | π (proporção da população) | p (proporção da amostra) |
Queremos calcular parâmetros populacionais, mas como demora muito e custa muito caro, usamos amostras para calcular estimativas pontuais.
Por exemplo, digamos que queremos estimar o peso médio de uma determinada espécie de tartaruga na Flórida. Como existem milhares de tartarugas na Flórida, seria extremamente demorado e caro pesar cada tartaruga individualmente. Em vez disso, poderíamos pegar uma amostra aleatória simples de 50 tartarugas e usar o peso médio das tartarugas nessa amostra para estimar a verdadeira média populacional:

Se a média amostral for 150,4 libras, então nossa estimativa pontual da verdadeira média populacional de toda a espécie seria 150,4 libras.
A importância de amostras representativas
Quando coletamos uma amostra de uma população, idealmente queremos que a amostra se assemelhe a uma “miniversão” da nossa população.
Diz-se que uma amostra é representativa de uma população se as características dos indivíduos da amostra corresponderem de perto às características dos indivíduos da população geral.
Quando isso acontece, podemos generalizar com segurança os resultados da amostra para a população geral e podemos dizer que a estimativa pontual da amostra é uma estimativa imparcial do verdadeiro parâmetro da população.
Estimativas pontuais e intervalos de confiança
Embora uma estimativa pontual represente a nossa melhor estimativa possível de um parâmetro populacional verdadeiro, é improvável que corresponda exactamente ao parâmetro populacional.
No nosso exemplo anterior, não é garantido que o peso médio das tartarugas na amostra corresponda exactamente ao peso médio das tartarugas em toda a população. Por exemplo, podemos escolher uma amostra cheia de tartarugas de baixo peso ou talvez uma amostra cheia de tartarugas pesadas.
Assim, para capturar esta incerteza, podemos criar um intervalo de confiança – um intervalo de valores que provavelmente conterá um parâmetro populacional com um certo nível de confiança.
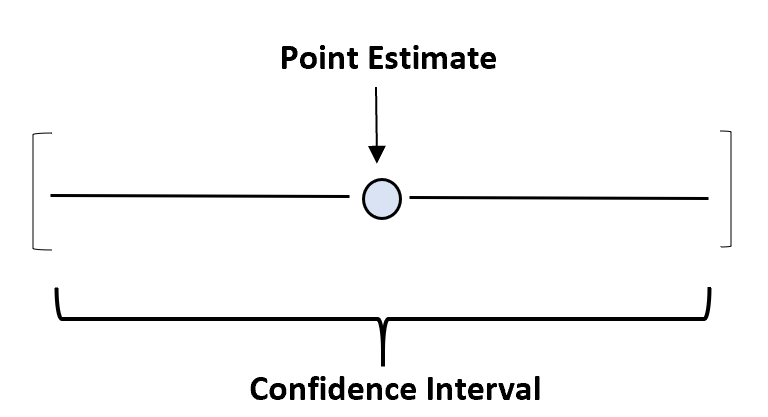
Por exemplo, podemos utilizar a nossa média amostral de 150,4 libras para estimar o verdadeiro peso médio de uma espécie de tartaruga. Nosso intervalo de confiança seria então uma faixa de valores – talvez de 145 libras a 155,8 libras.
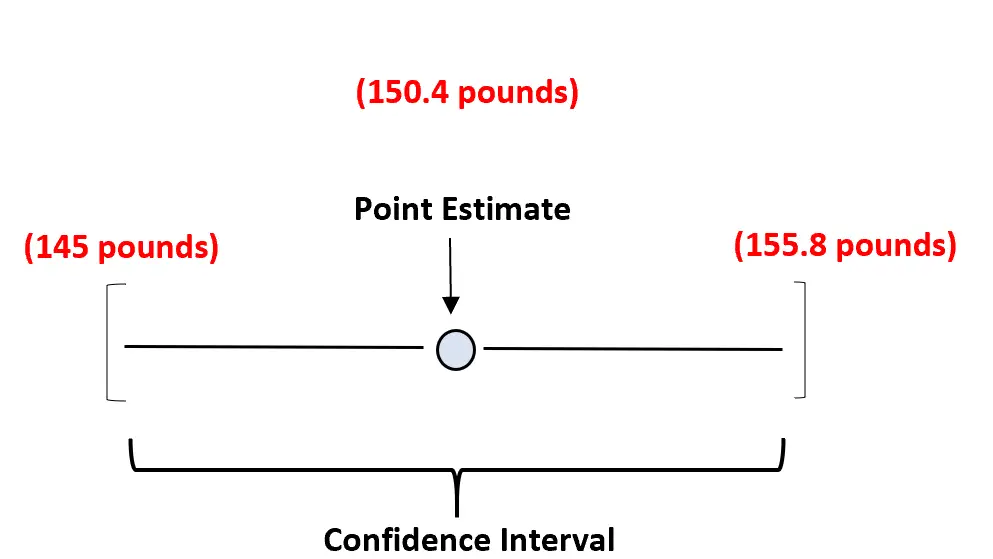
Nossa estimativa pontual é nossa melhor estimativa do verdadeiro peso médio da população e o intervalo de confiança fornece uma faixa de valores que provavelmente contém o verdadeiro peso médio da população.
Você pode aprender mais sobre intervalos de confiança aqui .
Recursos adicionais
Estatísticas vs. parâmetros: qual é a diferença?
População vs. amostra: qual é a diferença?
Uma introdução aos intervalos de confiança