Uma introdução à distribuição rayleigh
A distribuição Rayleigh é uma distribuição de probabilidade contínua usada para modelar variáveis aleatórias que só podem assumir valores iguais ou maiores que zero.
Tem a seguinte função de densidade de probabilidade:
f(x; σ) = (x/σ 2 )e -x 2 /(2σ 2 )
onde σ é o parâmetro de escala da distribuição.
Propriedades da distribuição Rayleigh
A distribuição Rayleigh tem as seguintes propriedades:
- Média: σ√ π/2
- Desvio: ((4-π)/2)σ 2
- Modo: σ
Como π tem um valor numérico conhecido, podemos simplificar as propriedades da seguinte forma:
- Média: 1,253σ
- Desvio: 0,429σ 2
- Modo: σ
Visualização da distribuição Rayleigh
O gráfico a seguir mostra o formato da distribuição Rayleigh, pois ela assume valores diferentes para o parâmetro de escala:
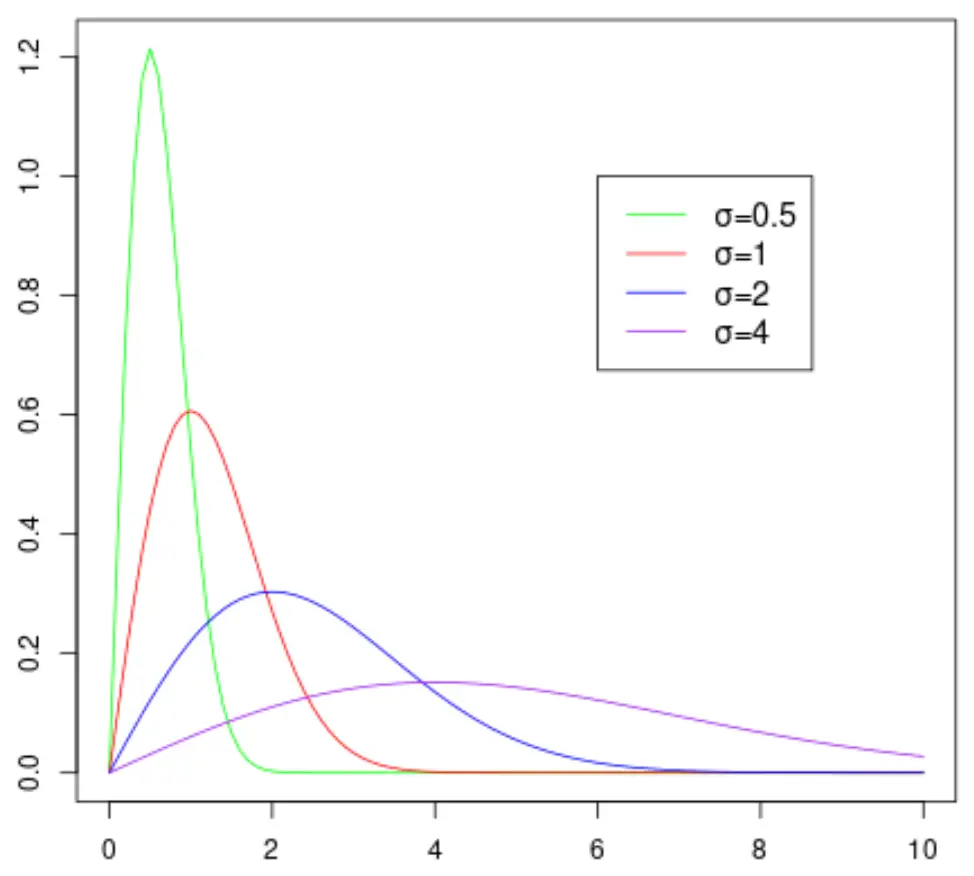
Observe que quanto maior o valor do parâmetro de escala σ, mais ampla se torna a distribuição.
Bônus: Para quem tiver curiosidade, utilizamos o seguinte código R para gerar o gráfico acima:
#load VGAM package library (VGAM) #create density plots curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green') curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE) curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE) curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE) #add legend legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"), col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)
Relacionamento com outras distribuições
A distribuição Rayleigh tem a seguinte relação com outras distribuições de probabilidade:
1. Quando o parâmetro de escala (σ) é igual a 1, a distribuição Rayleigh é igual a uma distribuição Qui-quadrado com 2 graus de liberdade.
2. A distribuição Rayleigh é um caso especial da distribuição Weibull com parâmetro de forma k = 2.
3. A distribuição Rayleigh com parâmetro de escala σ é igual à distribuição Rice com Rice(0, σ).
Formulários
Na prática, a distribuição Rayleigh é usada em diversas aplicações, incluindo:
1. A distribuição Rayleigh é usada para modelar o comportamento das ondas no oceano, incluindo o tempo que as ondas levam para atingir a crista e a altura máxima atingida pelas ondas.
2. A distribuição Rayleigh é usada para modelar o comportamento dos dados de fundo em imagens de ressonância magnética, mais comumente conhecidas como MRI.
3. A distribuição Rayleigh é utilizada no campo da nutrição para modelar a relação entre os níveis de nutrientes e a resposta nutricional em humanos e animais.
Recursos adicionais
Os tutoriais a seguir fornecem informações adicionais sobre outras distribuições em estatísticas:
Uma introdução à distribuição normal
Uma introdução à distribuição binomial
Uma introdução à distribuição de Poisson