Distribuição de bernoulli e distribuição binomial: qual a diferença?

Uma variável aleatória segue uma distribuição de Bernoulli se tiver apenas dois resultados possíveis: 0 ou 1.

Por exemplo, suponha que joguemos uma moeda uma vez. Deixe p . Isso significa que a probabilidade de dar coroa é 1- p .

Então, poderíamos escrever:

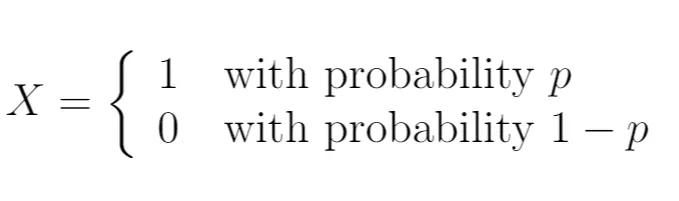
Neste caso, a variável aleatória X segue uma distribuição de Bernoulli. Só pode assumir dois valores possíveis.

Agora, se jogarmos uma moeda várias vezes, a soma das variáveis aleatórias de Bernoulli seguirá uma distribuição binomial.

Por exemplo, suponha que lançamos uma moeda 5 vezes e queremos saber a probabilidade de obter cara k vezes. Parece que a variável aleatória

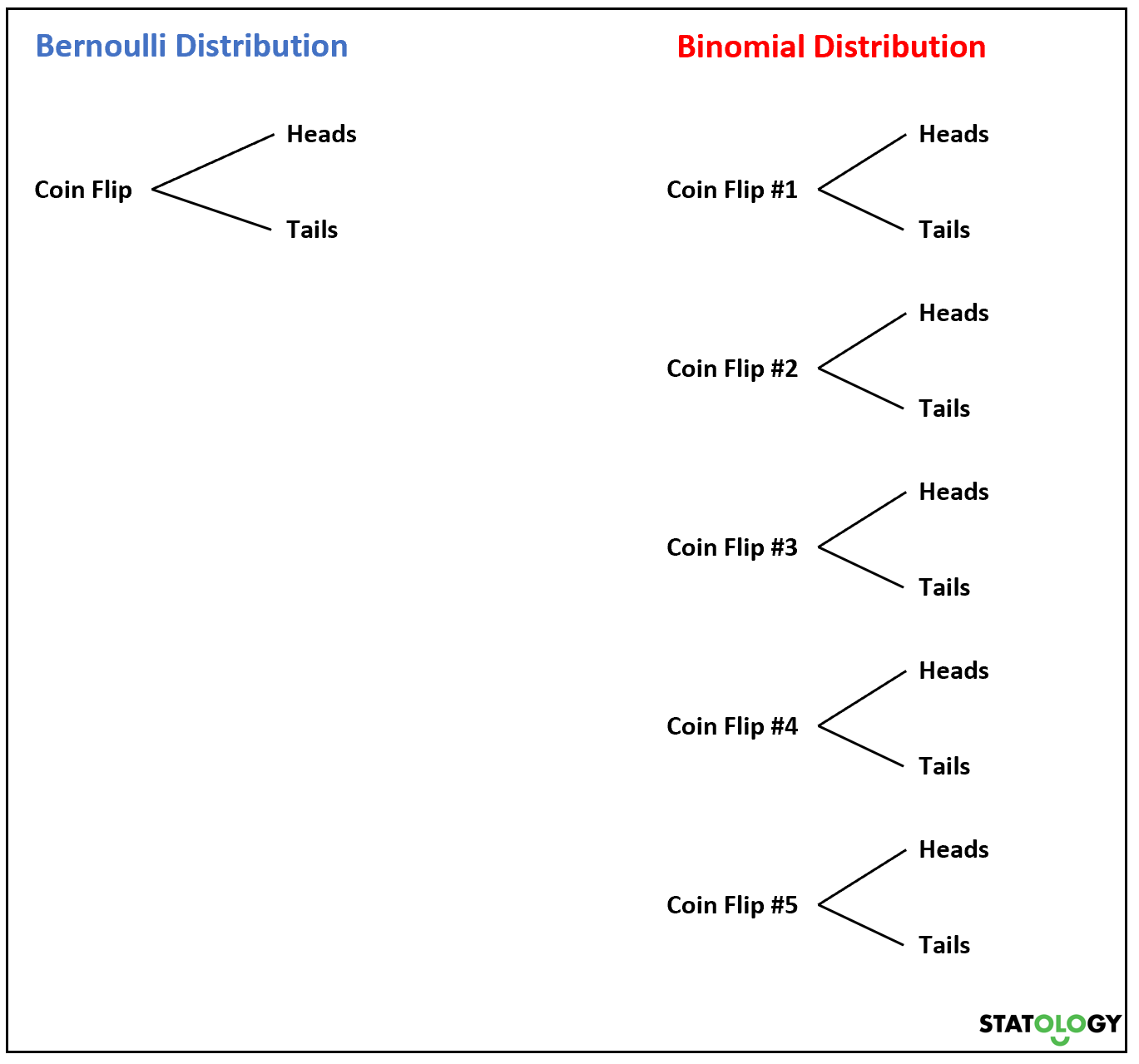
Se uma variável aleatória X segue uma distribuição binomial, então a probabilidade de X = k sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Ouro:

• n: número de tentativas
• k: número de sucessos
• p: probabilidade de sucesso em uma determinada tentativa
• _n C _k : o número de maneiras de obter k sucessos em n tentativas

Por exemplo, suponhamos que jogamos uma moeda 3 vezes. Podemos usar a fórmula acima para determinar a probabilidade de obter 0 cara durante essas 3 jogadas:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Quando n = 1 tentativa, a distribuição binomial é equivalente à distribuição de Bernoulli.

Anotações importantes

Aqui estão algumas notas importantes sobre a distribuição Bernoulli e Binomial:

1. Uma variável aleatória que segue uma distribuição de Bernoulli pode assumir apenas dois valores possíveis, mas uma variável aleatória que segue uma distribuição binomial pode assumir vários valores.

Por exemplo, em um único lançamento de moeda, teremos 0 ou 1 cara. Porém, numa série de 5 empates poderíamos ter 0, 1, 2, 3, 4 ou 5 caras.

2. Para que uma variável aleatória siga uma distribuição binomial, a probabilidade de “sucesso” em cada tentativa de Bernoulli deve ser igual e independente.

Por exemplo, se definirmos “sucesso” como dar cara, então a probabilidade de sucesso em cada lançamento é 0,5 e cada lançamento é independente – o resultado de um lançamento não afeta o resultado de outro.

Recursos adicionais

Uma introdução aos experimentos binomiais
Uma introdução à distribuição binomial
Compreendendo a forma de uma distribuição binomial