Correlação vs regressão: qual a diferença?

Correlação e regressão são dois termos estatísticos relacionados, mas não inteiramente iguais.

Neste tutorial, forneceremos uma breve explicação de ambos os termos e explicaremos como eles são semelhantes e diferentes.

O que é correlação?

A correlação mede a associação linear entre duas variáveis, x e y . Tem um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Por exemplo, suponha que temos o seguinte conjunto de dados que contém duas variáveis: (1) Horas estudadas e (2) Notas de exames recebidas por 20 alunos diferentes:

Se criássemos um gráfico de dispersão de horas estudadas versus resultados de exames, seria assim:

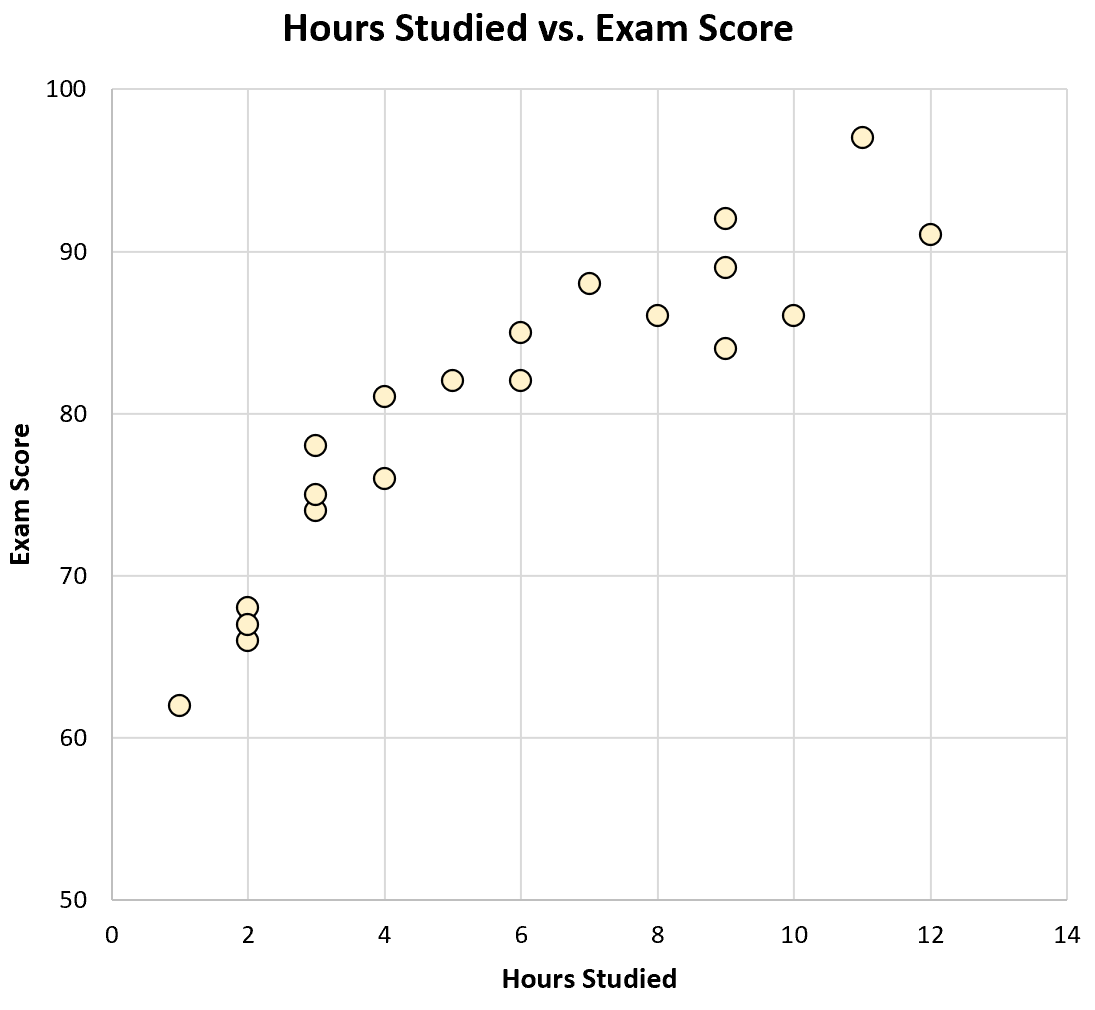
Só de olhar o gráfico podemos perceber que os alunos que estudam mais tendem a ter melhor desempenho nas provas. Ou seja, podemos perceber visualmente que existe uma correlação positiva entre as duas variáveis.

Usando uma calculadora, podemos ver que a correlação entre essas duas variáveis é r = 0,915 . Sendo este valor próximo de 1, confirma que existe uma forte correlação positiva entre as duas variáveis.

O que é regressão?

A regressão é um método que podemos usar para entender como a alteração dos valores da variável x afeta os valores da variável y .

Um modelo de regressão usa uma variável, x , como variável preditora e a outra variável, y , como variável de resposta . Em seguida, encontra uma equação da seguinte forma que melhor descreve a relação entre as duas variáveis:

ŷ = b ₀ + b ₁ x

Ouro:

• ŷ: o valor previsto da variável resposta
• b ₀ : A ordenada na origem (o valor de y quando x é igual a zero)
• b ₁ : O coeficiente de regressão (o aumento médio em y para um aumento de uma unidade em x)
• x: o valor da variável preditiva

Por exemplo, considere nosso conjunto de dados anterior:

Usando umacalculadora de regressão linear , descobrimos que a seguinte equação descreve melhor a relação entre essas duas variáveis:

Nota prevista no exame = 65,47 + 2,58*(horas estudadas)

A maneira de interpretar esta equação é:

• A nota prevista no exame para um aluno que estuda zero horas é 65,47 .
• O aumento médio da pontuação do exame associado a uma hora adicional de estudo é de 2,58 .

Também podemos usar esta equação para prever a pontuação que um aluno receberá com base no número de horas estudadas.

Por exemplo, um aluno que estuda 6 horas deverá receber nota 80,95 :

Nota prevista no exame = 65,47 + 2,58*(6) = 80,95 .

Também podemos representar esta equação como uma linha em um gráfico de dispersão:

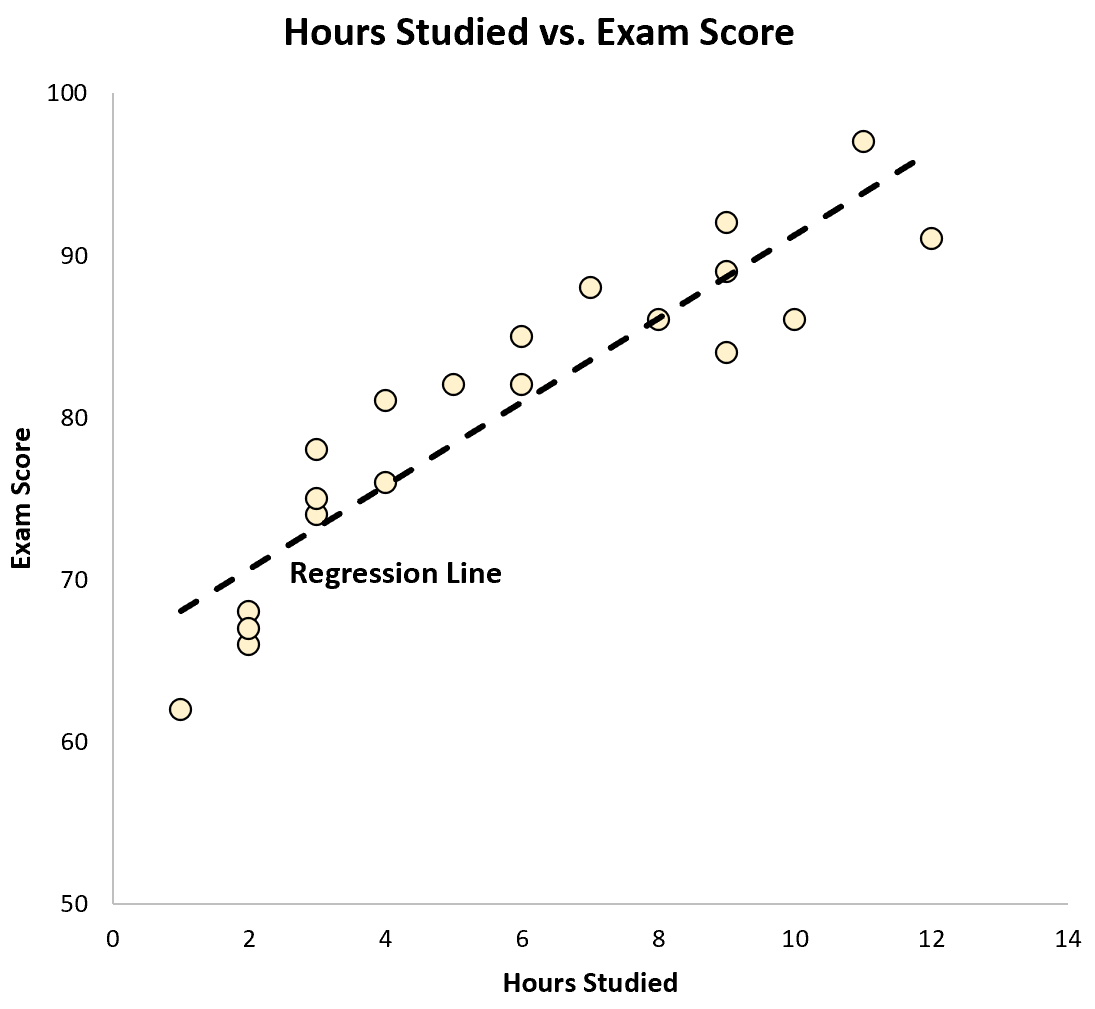
Podemos ver que a linha de regressão “se ajusta” muito bem aos dados.

Lembre-se anteriormente que a correlação entre essas duas variáveis foi r = 0,915 . Acontece que podemos elevar esse valor ao quadrado e obter um número chamado “r ao quadrado”, que descreve a proporção total de variância na variável de resposta que pode ser explicada pela variável preditora.

Neste exemplo, r ² = 0,915 ² = 0,837 . Isso significa que 83,7% da variação nas notas dos exames pode ser explicada pela quantidade de horas estudadas.

Correlação vs regressão: semelhanças e diferenças

Aqui está um resumo das semelhanças e diferenças entre correlação e regressão:

Semelhanças:

• Ambos quantificam a direção de um relacionamento entre duas variáveis.
• Ambos quantificam a força de uma relação entre duas variáveis.

Diferenças:

• A regressão é capaz de mostrar uma relação de causa e efeito entre duas variáveis. A correlação não faz isso.
• A regressão é capaz de usar uma equação para prever o valor de uma variável, com base no valor de outra variável. A correlação não faz isso.
• A regressão usa uma equação para quantificar a relação entre duas variáveis. A correlação usa um único número.

Recursos adicionais

Os tutoriais a seguir oferecem explicações mais detalhadas sobre os tópicos abordados neste artigo.

Uma introdução ao coeficiente de correlação de Pearson
Uma introdução à regressão linear simples
Calculadora de regressão linear simples
O que é um bom valor de R ao quadrado?