Randomização em estatísticas: definição e exemplo

No campo da estatística, a randomização refere-se ao ato de atribuir aleatoriamente os sujeitos do estudo a diferentes grupos de tratamento.

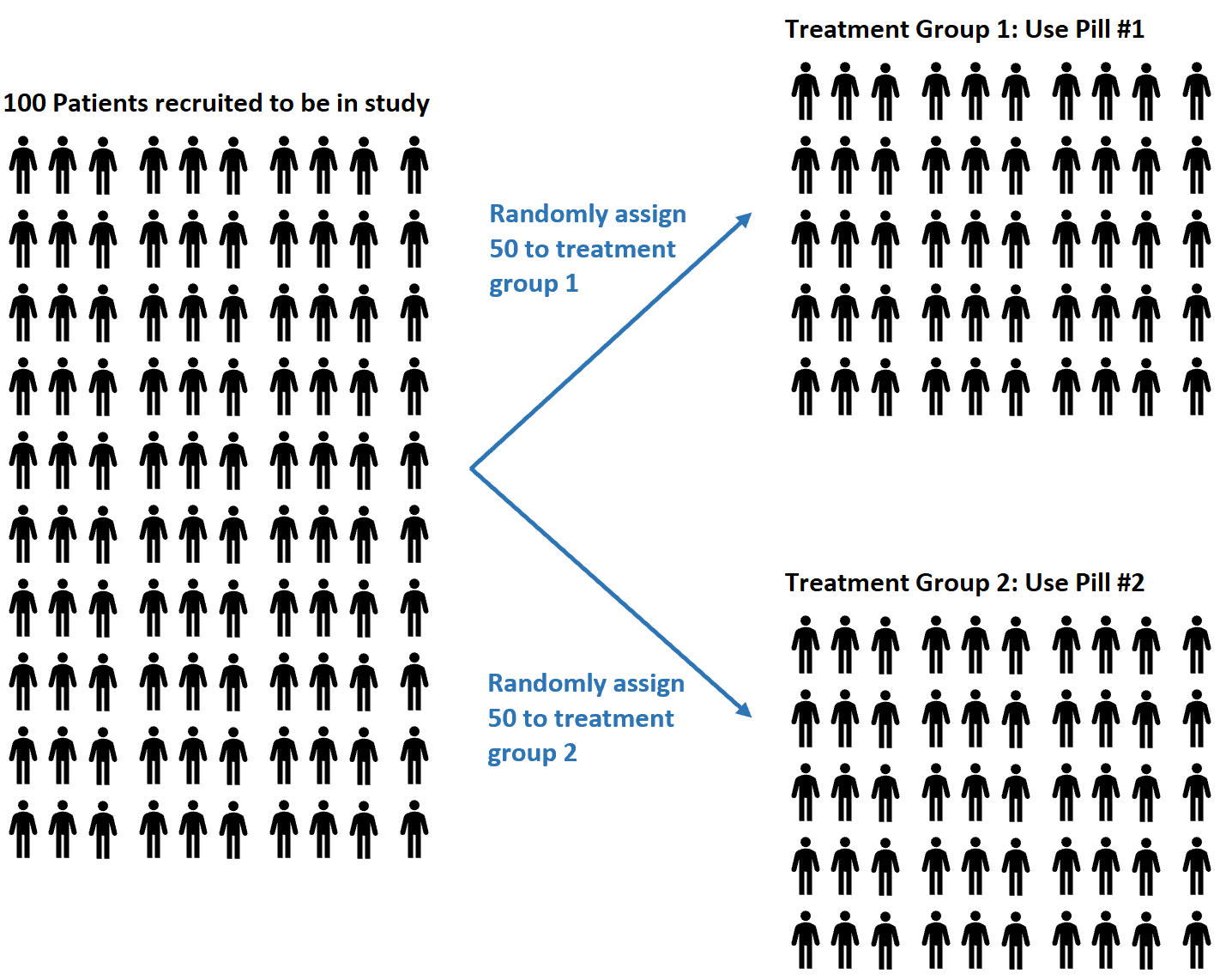
Por exemplo, suponhamos que os investigadores recrutem 100 indivíduos para participarem num estudo no qual esperam compreender se duas pílulas diferentes têm ou não efeitos diferentes sobre a pressão arterial.

Eles podem decidir usar um gerador de números aleatórios para designar aleatoriamente cada sujeito para usar a pílula nº 1 ou a pílula nº 2.

Vantagens da randomização

O objetivo da randomização é controlar variáveis ocultas – variáveis que não estão diretamente incluídas em uma análise, mas que ainda assim impactam a análise de alguma forma.

Por exemplo, se os investigadores estudarem os efeitos de duas pílulas diferentes na pressão arterial, as seguintes variáveis ocultas poderão afetar a análise:

• Roupas de smoking
• Dieta
• Exercício

Ao atribuir aleatoriamente os sujeitos aos grupos de tratamento, maximizamos a chance de que as variáveis ocultas afetem ambos os grupos de tratamento igualmente.

Isto significa que qualquer diferença na pressão arterial pode ser atribuída ao tipo de pílula e não ao efeito de uma variável oculta.

Randomização de bloco

Uma extensão da randomização é conhecida como randomização em bloco . Este é o processo de primeiro separar os sujeitos em blocos e depois usar a randomização para atribuir os sujeitos dentro dos blocos a diferentes tratamentos.

Por exemplo, se os investigadores quiserem saber se duas pílulas diferentes afetam a pressão arterial de forma diferente, podem primeiro separar todos os indivíduos em dois blocos com base no género: masculino ou feminino.

Então, em cada bloco, eles podem usar a randomização para designar aleatoriamente os indivíduos para usarem a pílula nº 1 ou a pílula nº 2.

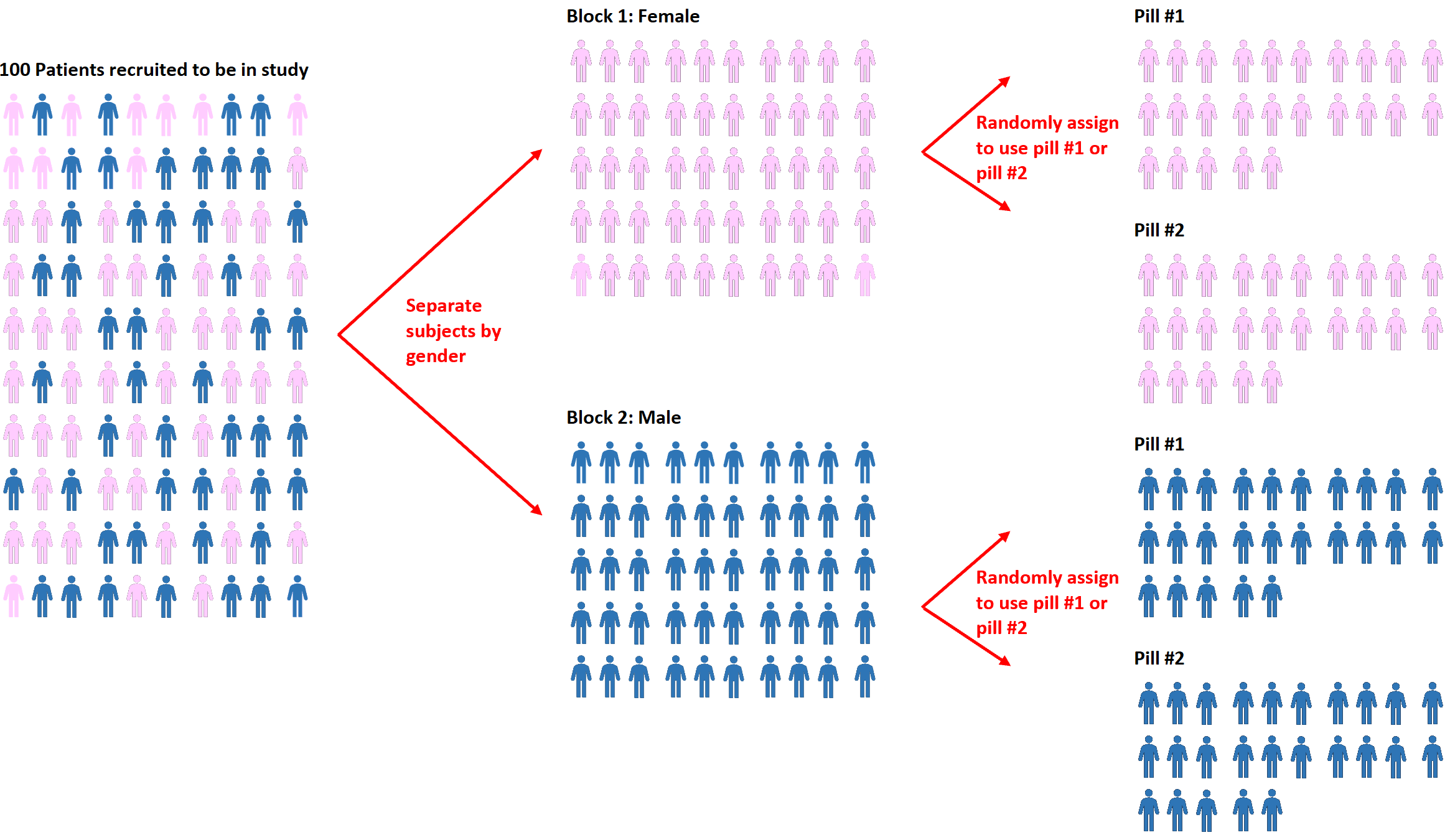
A vantagem desta abordagem é que os investigadores podem controlar diretamente qualquer efeito que o género possa ter sobre a pressão arterial, uma vez que sabemos que homens e mulheres tendem a responder de forma diferente a cada comprimido.

Ao utilizar o género como bloco, conseguimos eliminar esta variável como potencial fonte de variação. Se existirem diferenças na pressão arterial entre as duas pílulas, então podemos saber que o género não é a causa subjacente destas diferenças.

Recursos adicionais

Bloqueio nas estatísticas: definição e exemplo
Randomização de blocos permutados: definição e exemplo
Variáveis ocultas: definição e exemplos