Como calcular o erro padrão de regressão no excel
Ajustamos um modelo de regressão linear , o modelo assume a seguinte forma:
Y = β 0 + β 1 X + … + β i
onde ϵ é um termo de erro independente de X.
Não importa como X pode ser usado para prever os valores de Y, sempre haverá erros aleatórios no modelo.
Uma forma de medir a dispersão desse erro aleatório é utilizar o erro padrão do modelo de regressão , que é uma forma de medir o desvio padrão dos resíduos ϵ.
Este tutorial fornece um exemplo passo a passo de como calcular o erro padrão de um modelo de regressão no Excel.
Etapa 1: crie os dados
Para este exemplo, criaremos um conjunto de dados contendo as seguintes variáveis para 12 alunos diferentes:
- Resultado de exame
- Horas gastas estudando
- Turma atual
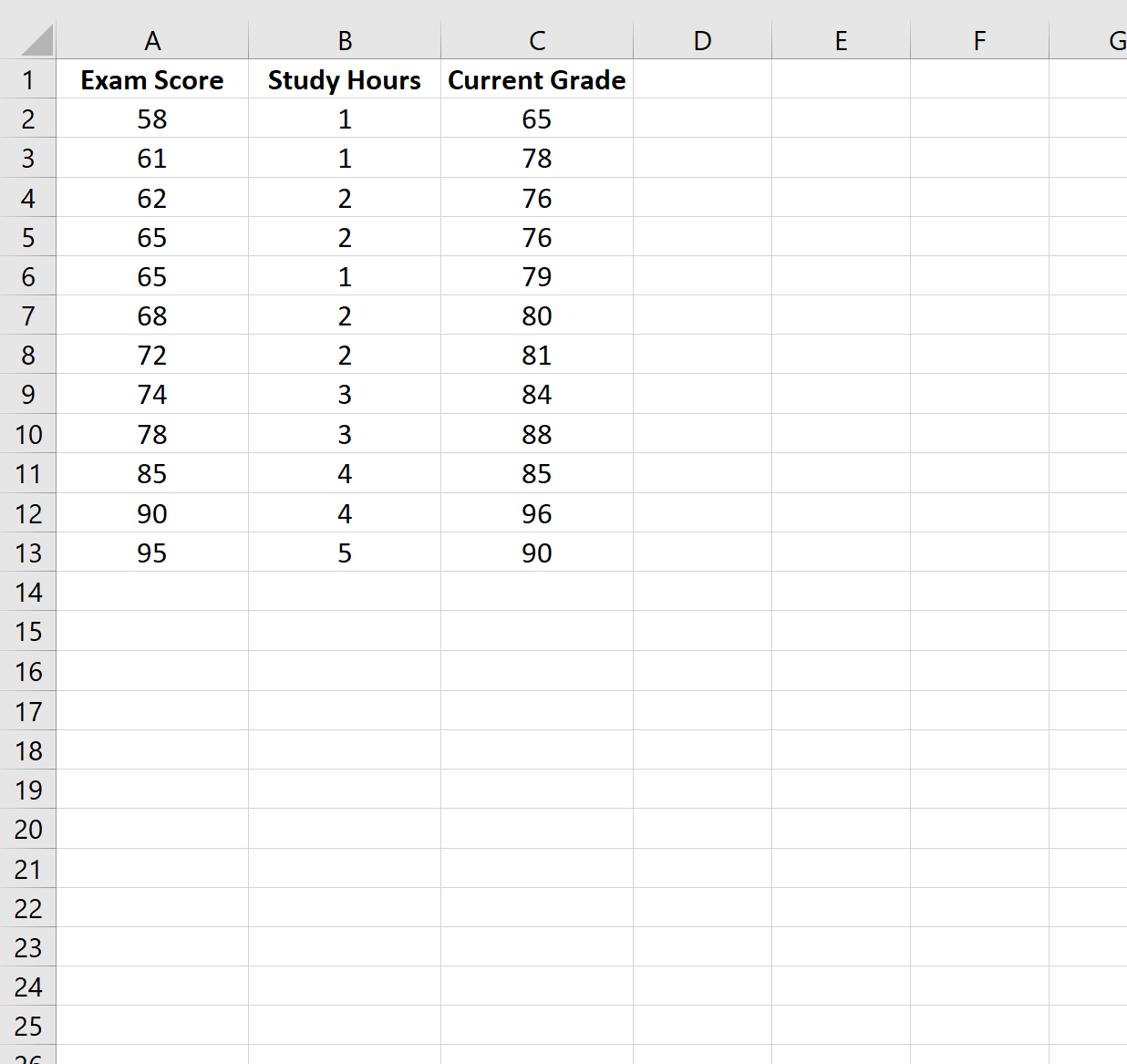
Passo 2: Ajustar o modelo de regressão
A seguir, ajustaremos um modelo de regressão linear múltipla usando a nota do exame como variável de resposta e as horas de estudo e a nota atual como variáveis preditoras.
Para fazer isso, clique na guia Dados na faixa superior e clique em Análise de dados :

Se esta opção não estiver disponível, você deverá primeiro carregar o Data Analysis ToolPak .
Na janela que aparece, selecione Regressão . Na nova janela que aparece, forneça as seguintes informações:
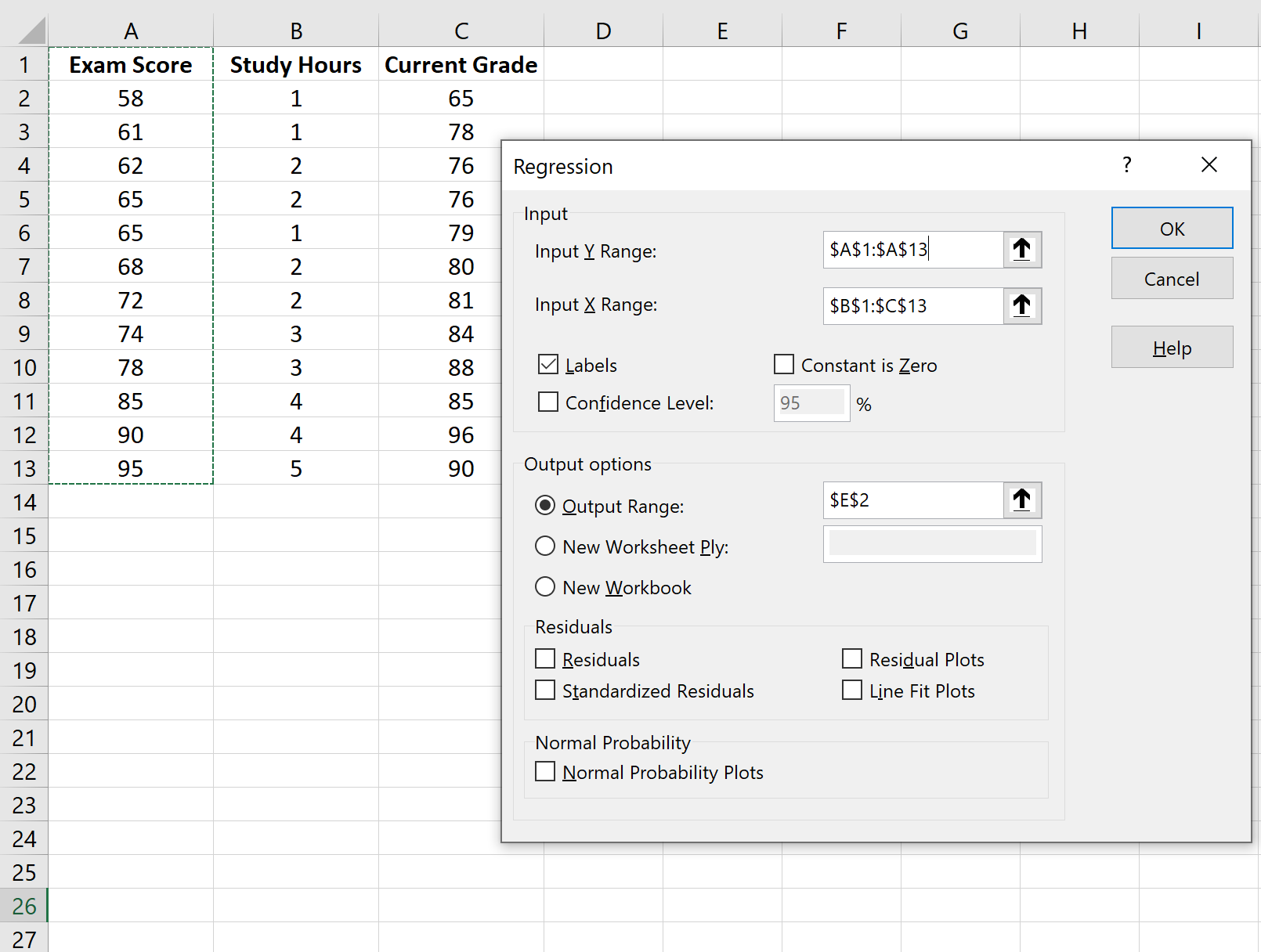
Depois de clicar em OK , a saída do modelo de regressão aparecerá:
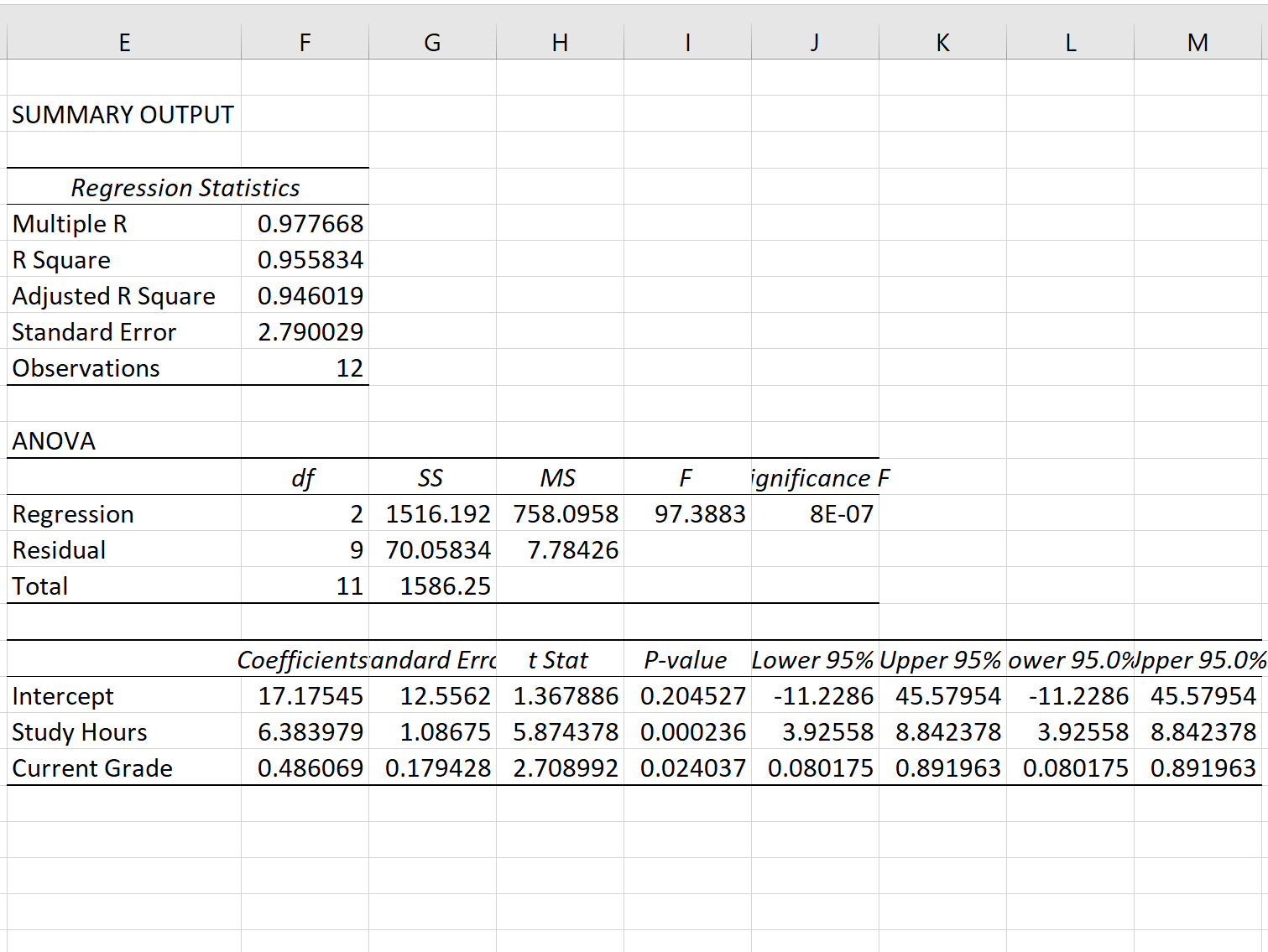
Etapa 3: Interpretar o erro padrão de regressão
O erro padrão do modelo de regressão é o número próximo ao erro padrão :
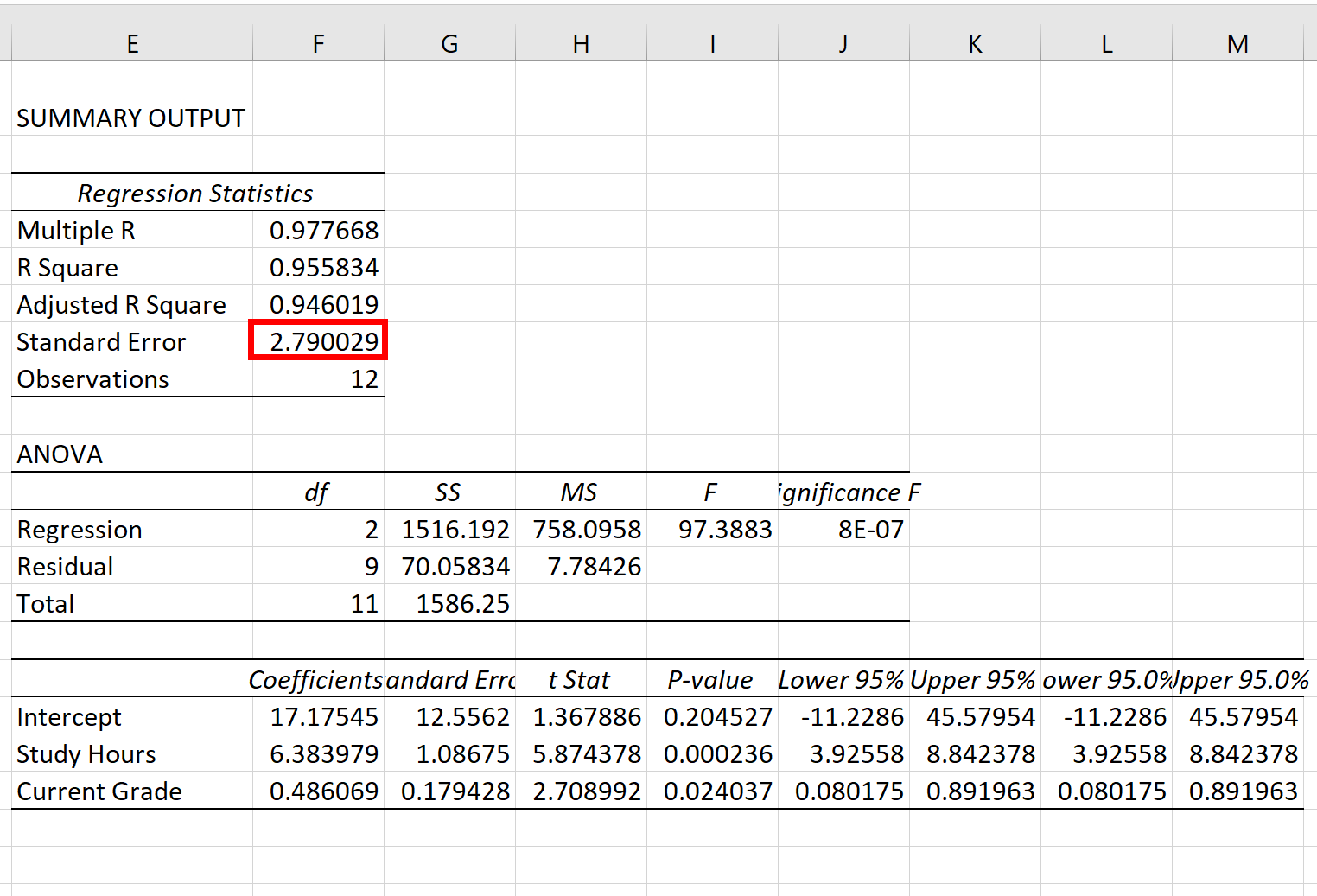
O erro padrão deste modelo de regressão específico é 2,790029 .
Este número representa a distância média entre os resultados reais do exame e os resultados do exame previstos pelo modelo.
Observe que alguns resultados de exames estarão mais de 2,79 unidades distantes da pontuação prevista, enquanto outros estarão mais próximos. Mas, em média, a distância entre os resultados reais dos exames e os resultados previstos é 2,790029 .
Observe também que um erro padrão de regressão menor indica que um modelo de regressão se ajusta melhor a um conjunto de dados.
Portanto, se ajustarmos um novo modelo de regressão ao conjunto de dados e obtivermos um erro padrão de, digamos, 4,53 , esse novo modelo seria menos eficaz na previsão de notas em exames do que o modelo anterior.
Recursos adicionais
Outra forma comum de medir a precisão de um modelo de regressão é usar R-quadrado. Confira este artigo para obter uma boa explicação sobre os benefícios de usar o erro padrão de regressão para medir a precisão versus R-quadrado.