Regressão polinomial no planilhas google (passo a passo)

A análise de regressão é usada para quantificar a relação entre uma ou mais variáveis preditoras e uma variável de resposta .

O tipo mais comum de análise de regressão é a regressão linear simples , usada quando uma variável preditora e uma variável resposta possuem um relacionamento linear.

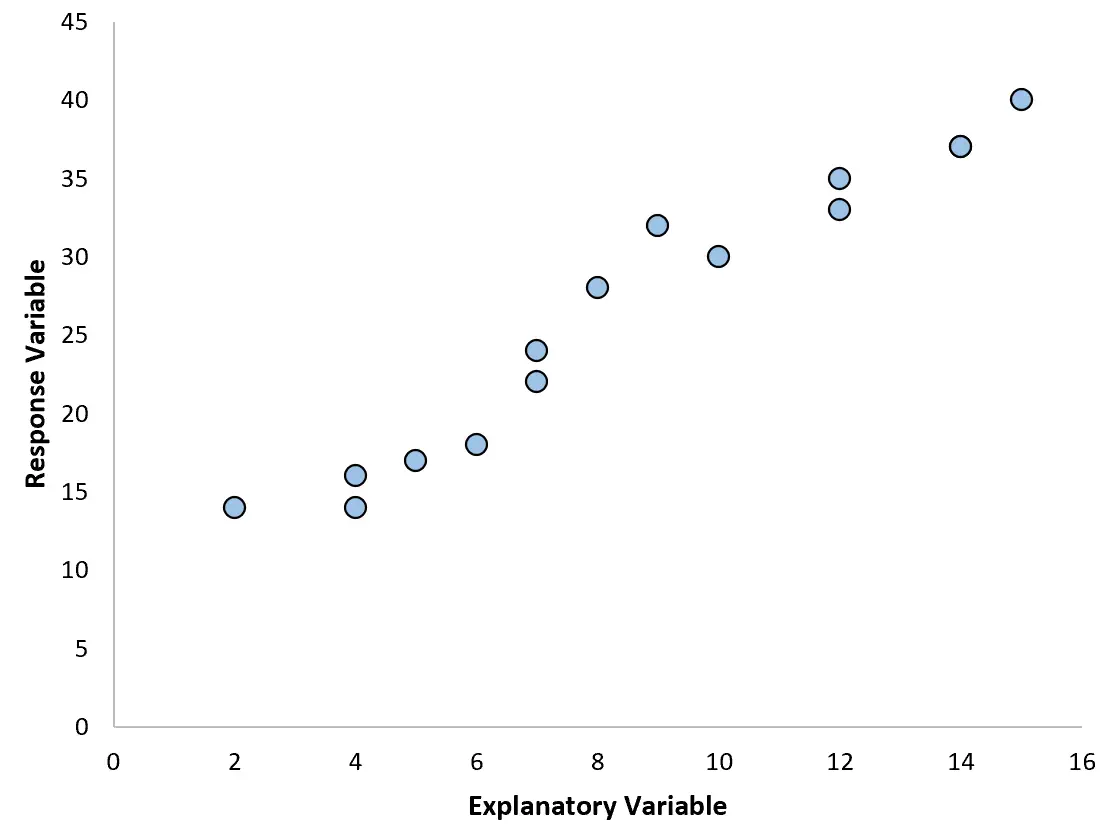
No entanto, às vezes a relação entre uma variável preditora e uma variável de resposta é não linear.

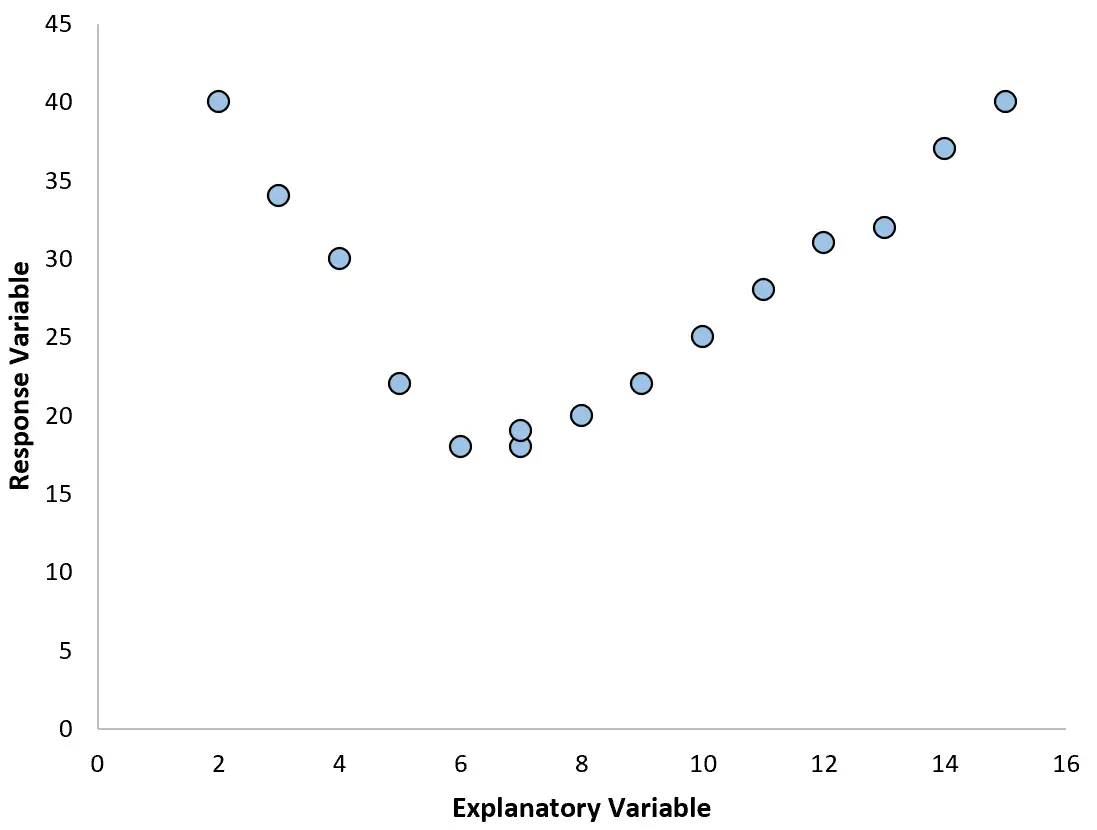
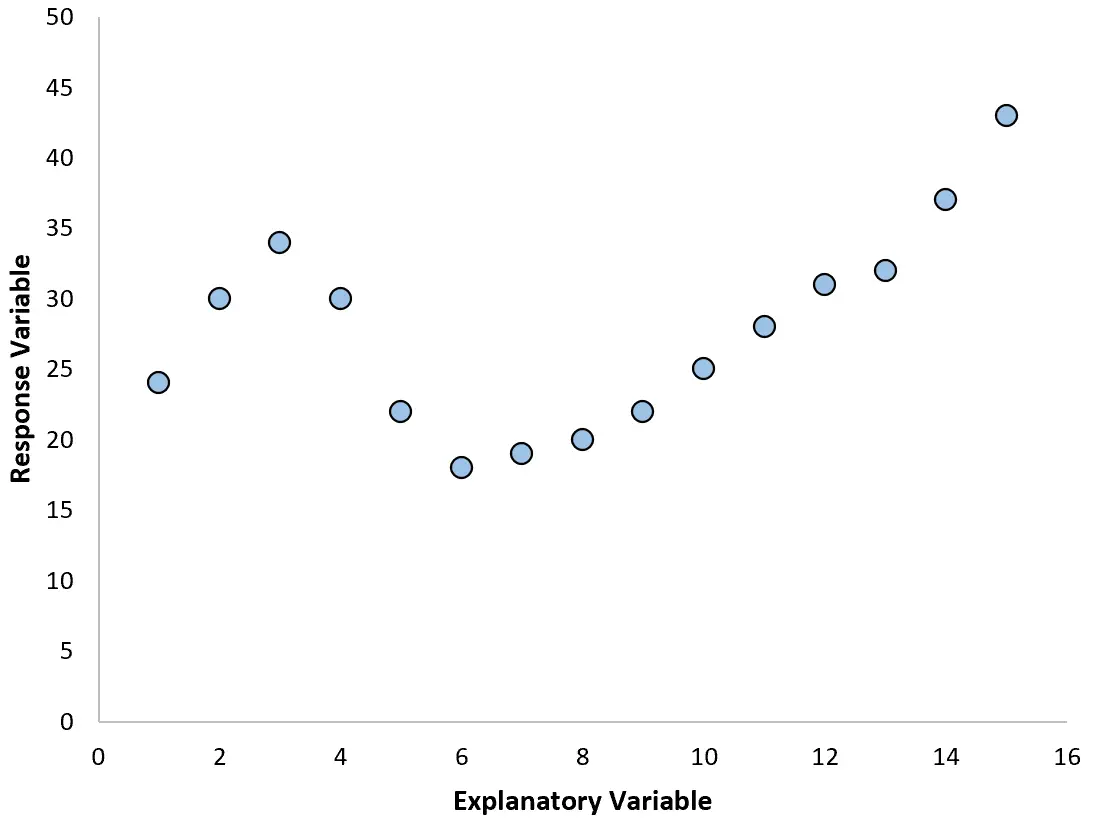
Nestes casos, faz sentido utilizar a regressão polinomial , que pode dar conta da relação não linear entre as variáveis.

Este tutorial fornece um exemplo passo a passo de como realizar regressão polinomial no Planilhas Google.

Etapa 1: crie os dados

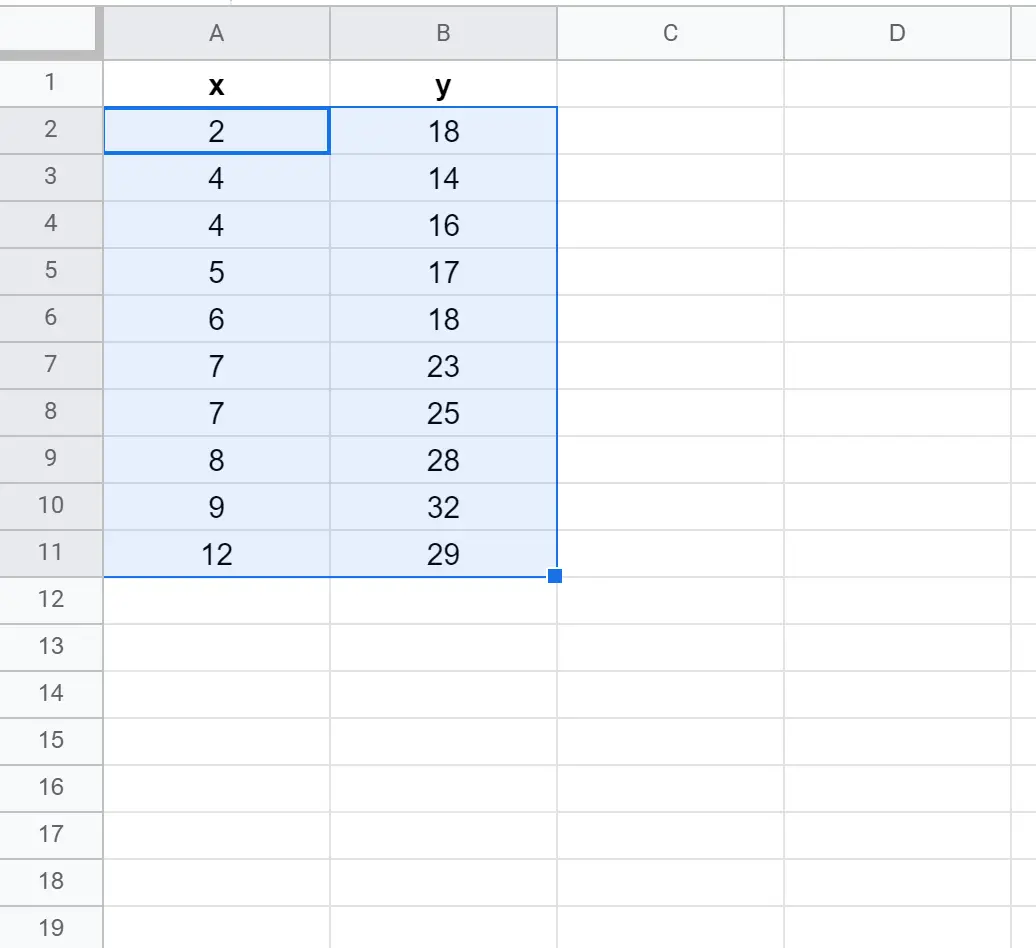
Primeiro, vamos criar um conjunto de dados falso com os seguintes valores:

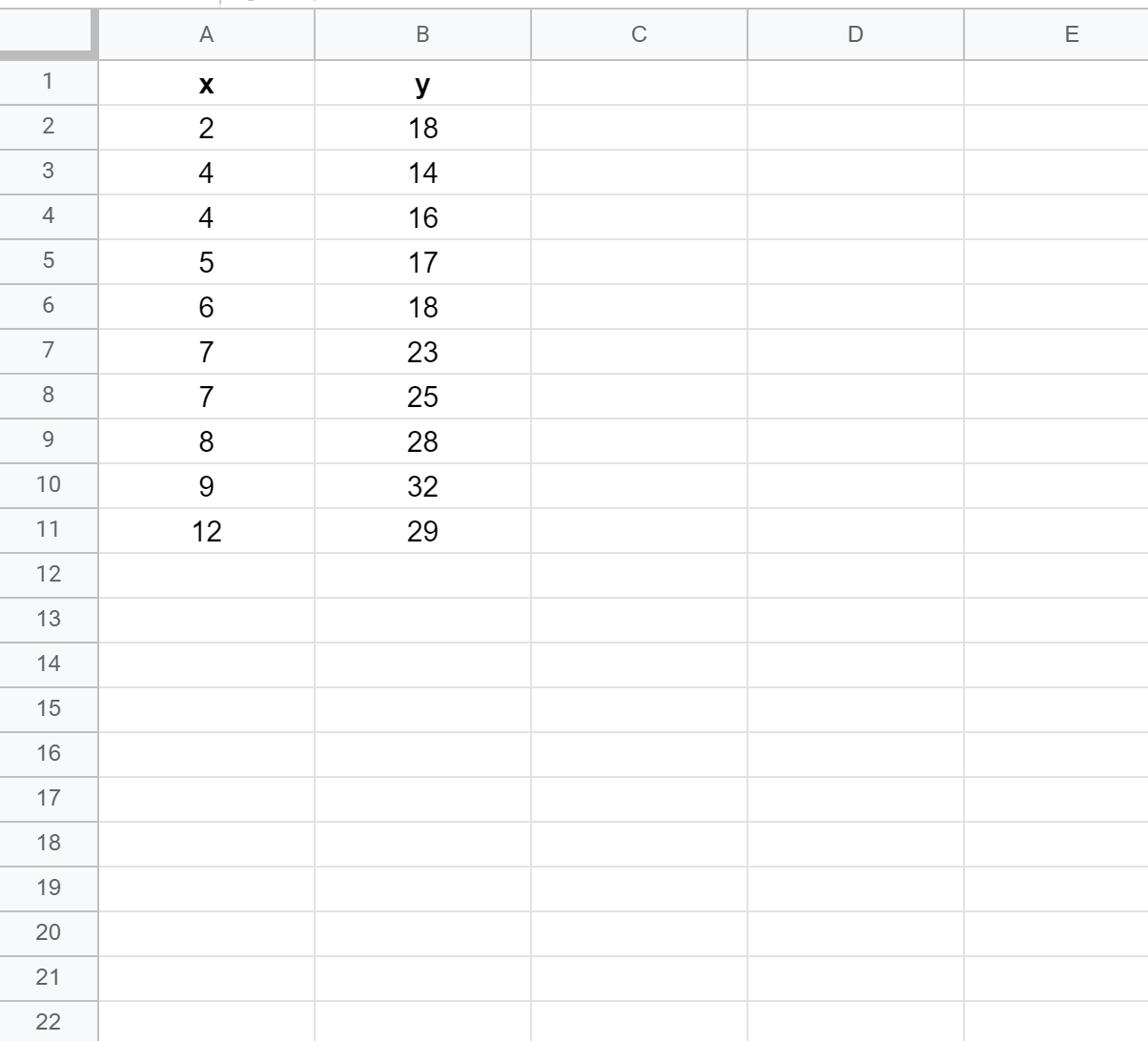
Etapa 2: crie um gráfico de dispersão

A seguir, criaremos um gráfico de dispersão para visualizar os dados.

Primeiro, destaque as células A2:B11 da seguinte forma:

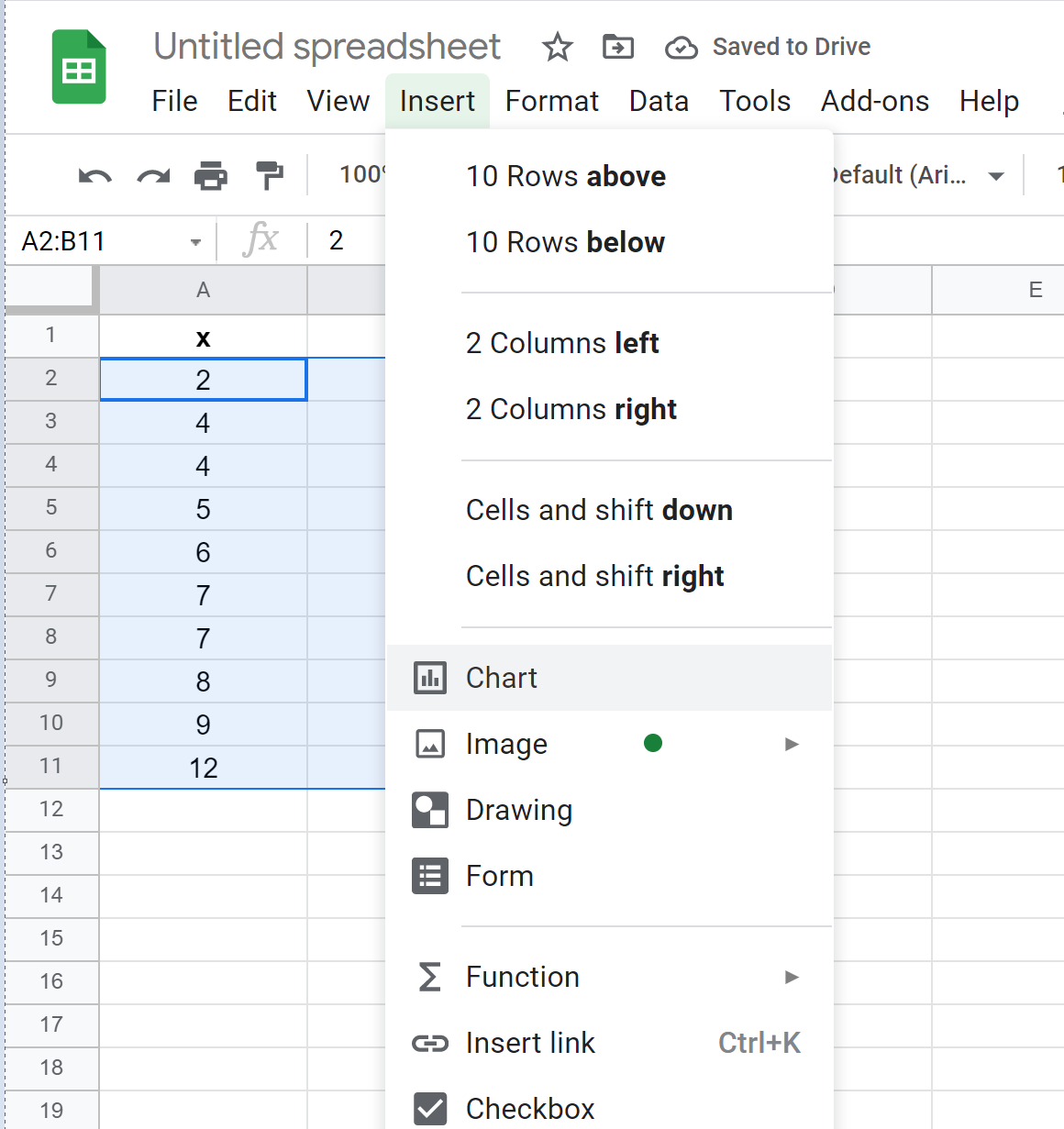
Em seguida, clique na guia Inserir e clique em Gráfico no menu suspenso:

Por padrão, o Planilhas Google inserirá um gráfico de dispersão:

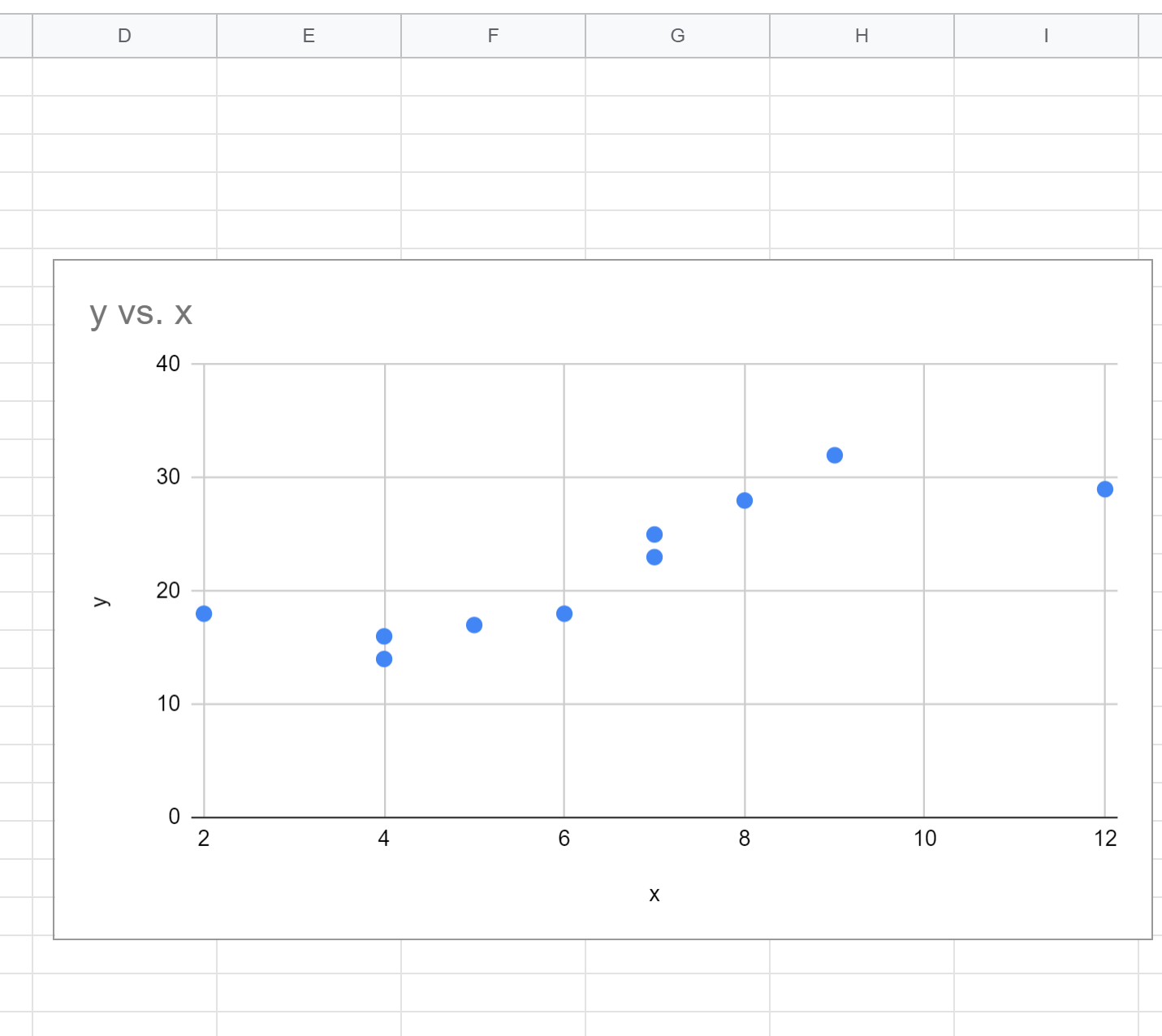
Etapa 3: Encontre a equação de regressão polinomial

Em seguida, clique duas vezes em qualquer lugar do gráfico de dispersão para exibir a janela do editor de gráfico à direita:

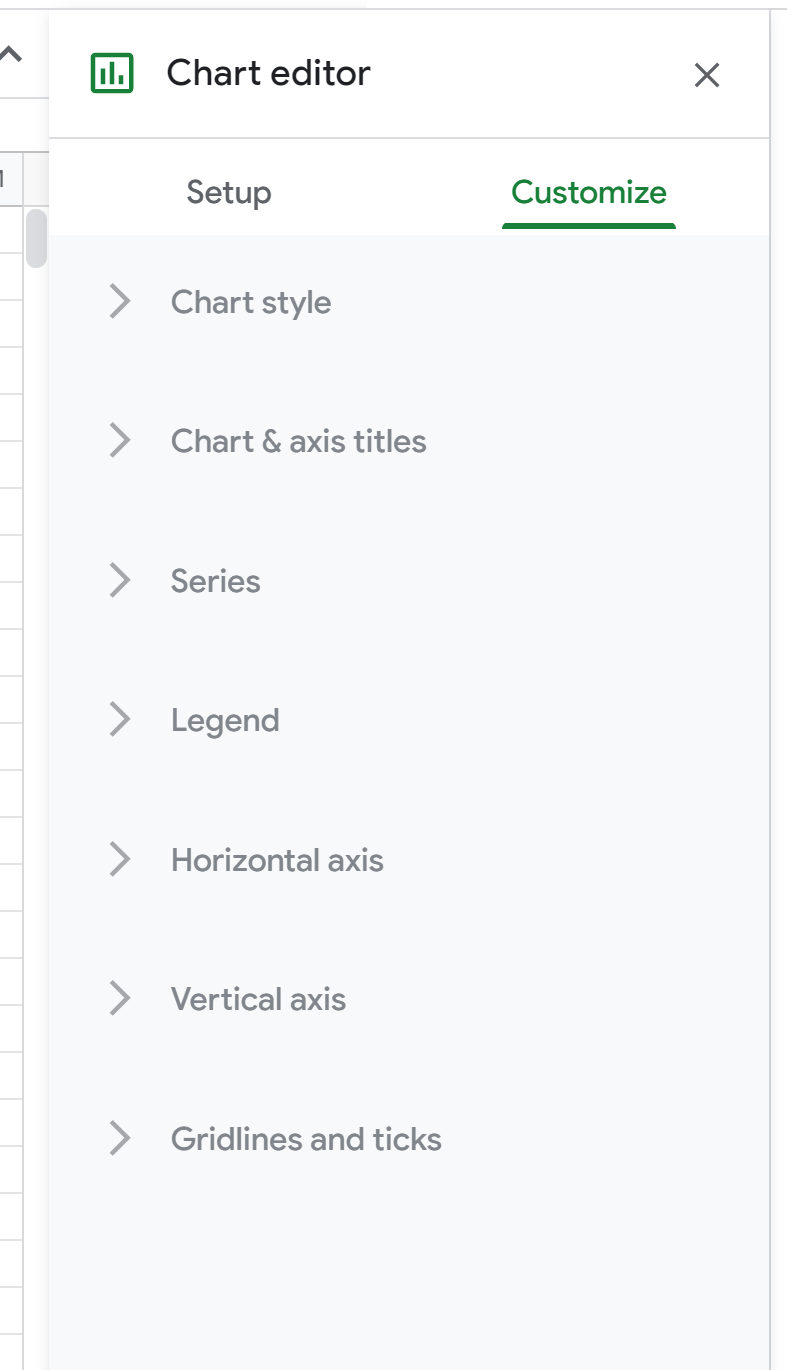
Em seguida, clique em Série . Em seguida, role para baixo e marque a caixa ao lado de Trendline e altere o Type para Polynomial . Para Label, escolha Use Equation e marque a caixa ao lado de Show ^R2 .

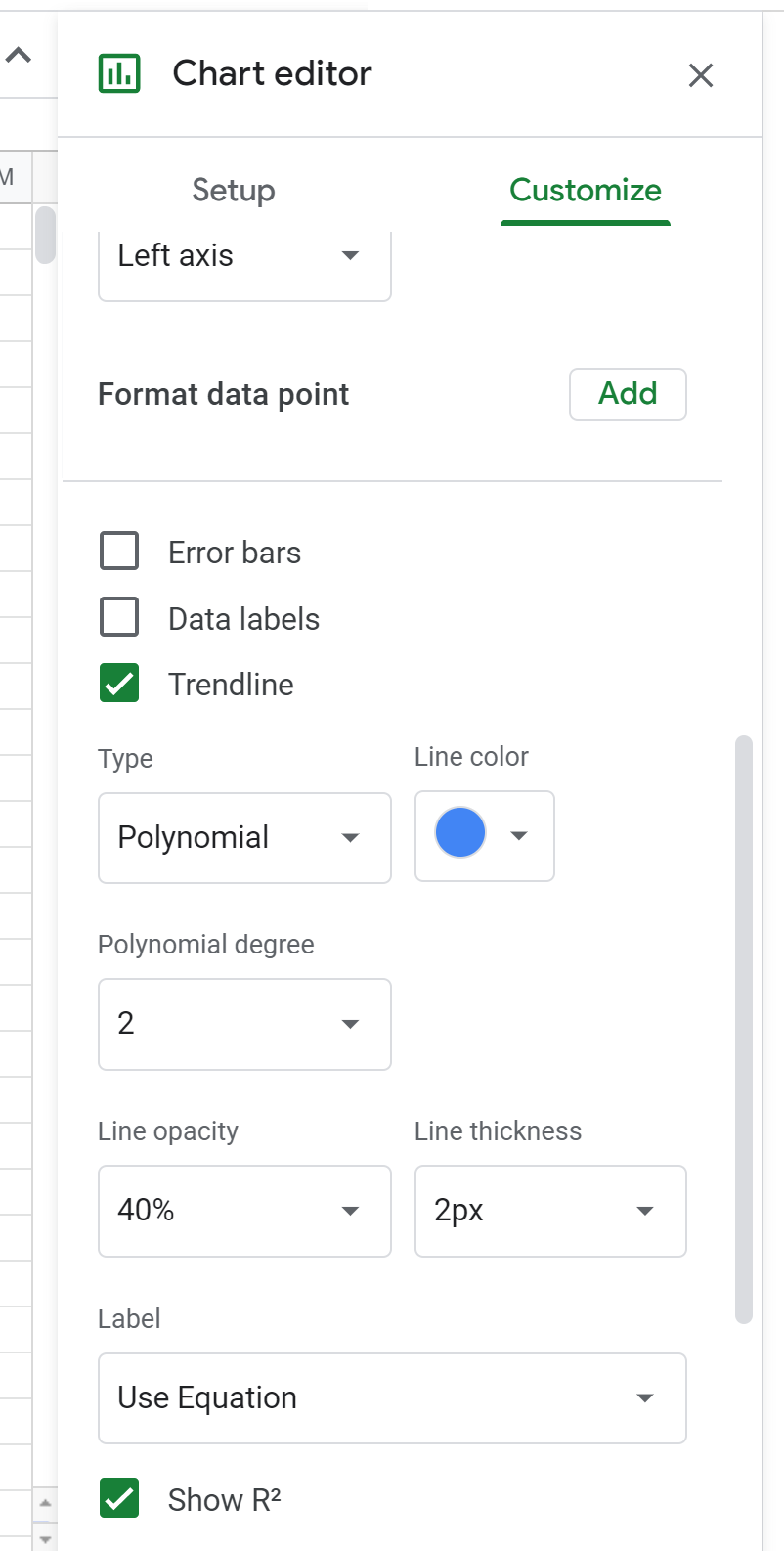
Isso fará com que a seguinte fórmula apareça acima do gráfico de dispersão:

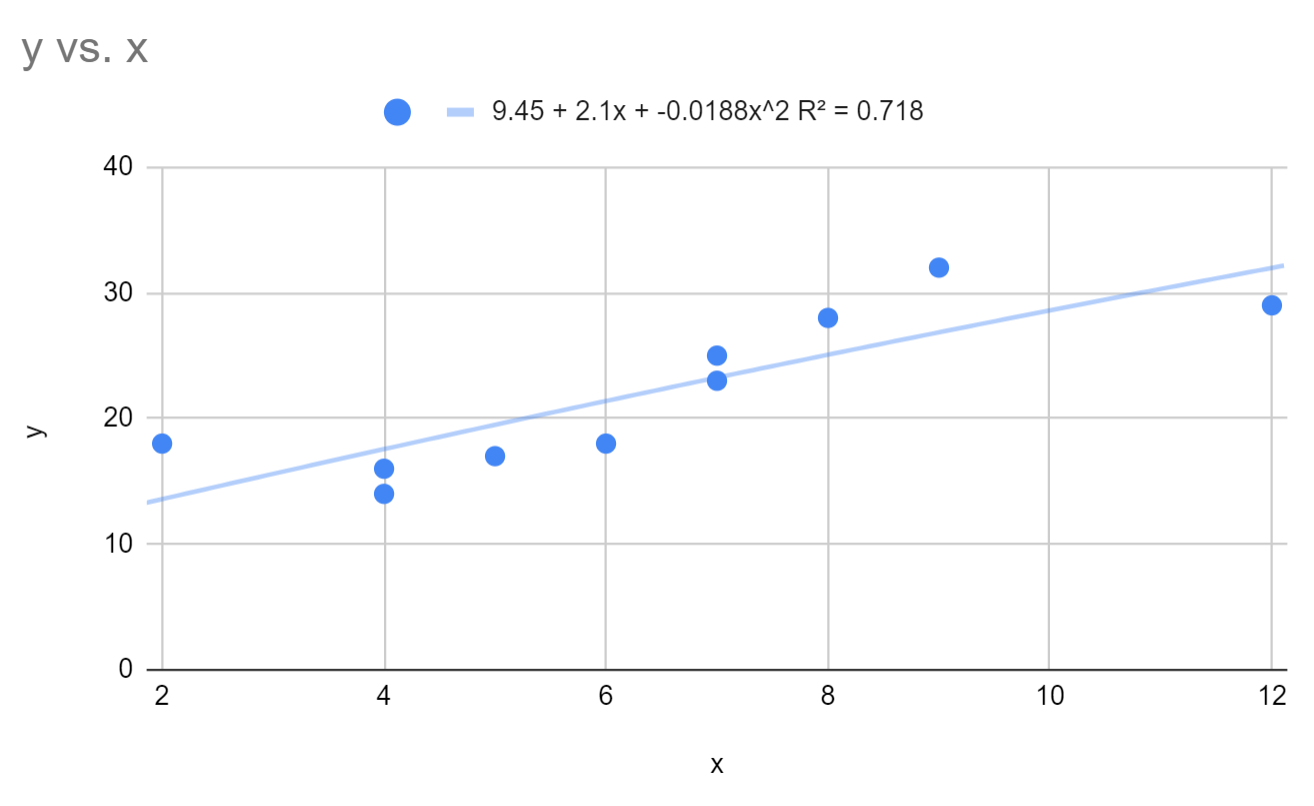
Podemos ver que a equação de regressão polinomial ajustada é:

y = 9,45 + 2,1x – 0,0188x ²

O R ao quadrado para este modelo é 0,718 .

Lembre-se de que R ao quadrado nos diz a porcentagem de variação na variável resposta que pode ser explicada pelas variáveis preditoras. Quanto maior o valor, melhor o modelo.

A seguir, altere o grau do polinômio para 3 no editor gráfico:

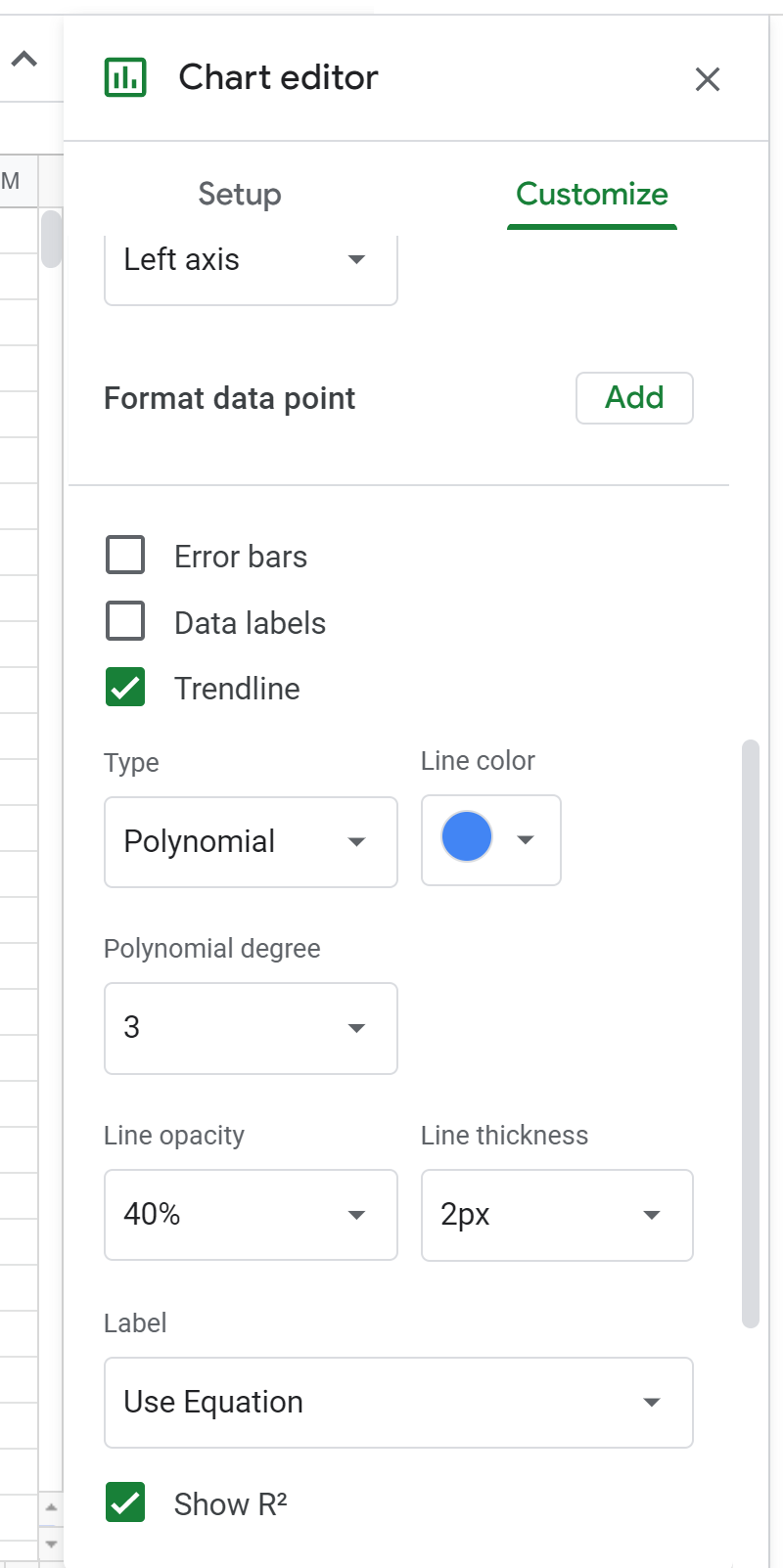
Isso fará com que a seguinte fórmula apareça acima do gráfico de dispersão:

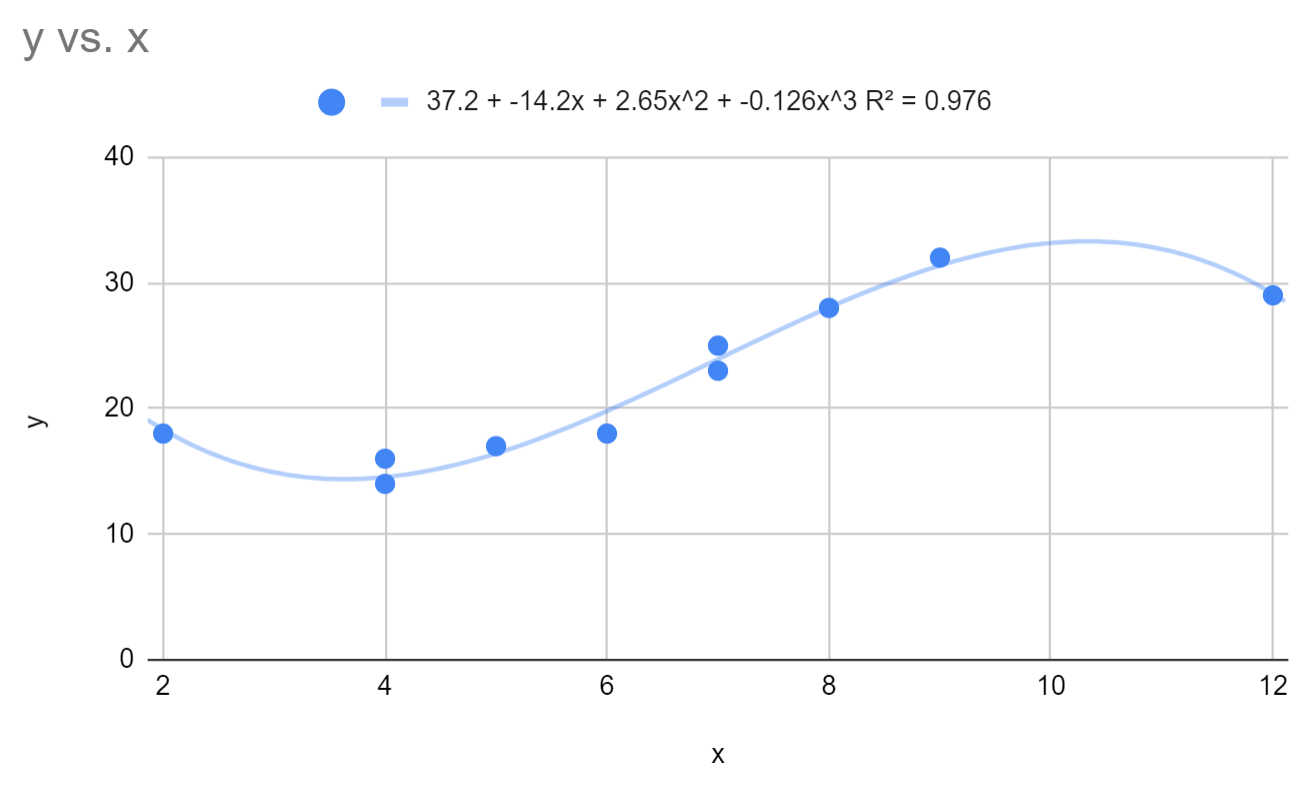
Isso altera a equação de regressão polinomial ajustada para:

y = 37,2 – 14,2x + 2,64x ² – 0,126x ³

O R ao quadrado para este modelo é 0,976 .

Observe que o R-quadrado deste modelo é significativamente maior do que o do modelo de regressão polinomial com grau 2. Isso sugere que este modelo de regressão é significativamente melhor na captura da tendência dos dados subjacentes.

Se você alterar o grau do polinômio para 4, o R ao quadrado mal aumentará para 0,981 . Isto sugere que um modelo de regressão polinomial de grau 3 é suficiente para capturar a tendência nestes dados.

Podemos usar a equação de regressão ajustada para encontrar o valor esperado da variável resposta, dado um determinado valor da variável preditora. Por exemplo, se x = 4 então o valor esperado para y seria:

y = 37,2 – 14,2(4) + 2,64(4) ² – 0,126(4) ³ = 14,576

Você pode encontrar outros tutoriais do Planilhas Google nesta página .