Regressão logarítmica em r (passo a passo)
A regressão logarítmica é um tipo de regressão usada para modelar situações em que o crescimento ou declínio acelera rapidamente no início e depois diminui com o tempo.
Por exemplo, o gráfico a seguir mostra um exemplo de decaimento logarítmico:

Para este tipo de situação, a relação entre uma variável preditora e uma variável resposta poderia ser bem modelada utilizando regressão logarítmica.
A equação para um modelo de regressão logarítmica assume a seguinte forma:
y = a + b*ln(x)
Ouro:
- y: a variável de resposta
- x: a variável preditiva
- a, b: os coeficientes de regressão que descrevem a relação entre x e y
O exemplo passo a passo a seguir mostra como realizar a regressão logarítmica em R.
Etapa 1: crie os dados
Primeiro, vamos criar dados falsos para duas variáveis: x e y :
x=1:15 y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)
Etapa 2: visualize os dados
A seguir, vamos criar um gráfico de dispersão rápido para visualizar a relação entre x e y :
plot(x, y)
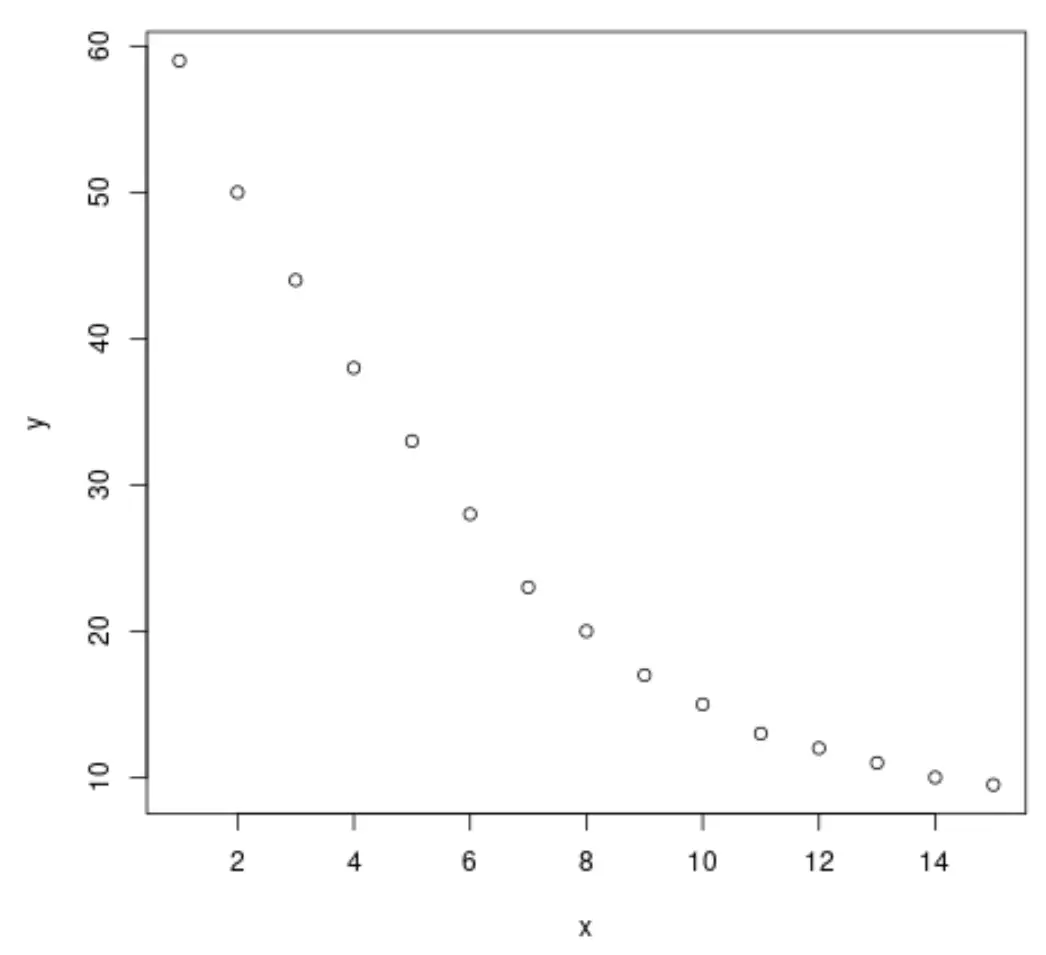
No gráfico, podemos ver que existe um padrão claro de decaimento logarítmico entre as duas variáveis. O valor da variável de resposta, y , diminui rapidamente no início e depois diminui com o tempo.
Portanto, parece sensato ajustar uma equação de regressão logarítmica para descrever a relação entre as variáveis.
Etapa 3: Ajustar o modelo de regressão logarítmica
A seguir, usaremos a função lm() para ajustar um modelo de regressão logarítmica, usando o logaritmo natural de x como variável preditora e y como variável de resposta.
#fit the model model <- lm(y ~ log (x)) #view the output of the model summary(model) Call: lm(formula = y ~ log(x)) Residuals: Min 1Q Median 3Q Max -4.069 -1.313 -0.260 1.127 3.122 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 63.0686 1.4090 44.76 1.25e-15 *** log(x) -20.1987 0.7019 -28.78 3.70e-13 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 2.054 on 13 degrees of freedom Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13
O valor F geral do modelo é 828,2 e o valor p correspondente é extremamente baixo (3.702e-13), indicando que o modelo como um todo é útil.
Usando os coeficientes da tabela de saída, podemos ver que a equação de regressão logarítmica ajustada é:
y = 63,0686 – 20,1987 * ln(x)
Podemos usar esta equação para prever a variável de resposta, y , com base no valor da variável preditora, x . Por exemplo, se x = 12, então preveríamos que y seria 12,87 :
y = 63,0686 – 20,1987 * ln(12) = 12,87
Bônus: sinta-se à vontade para usar esta calculadora de regressão logarítmica online para calcular automaticamente a equação de regressão logarítmica para um determinado preditor e variável de resposta.
Passo 4: Visualize o modelo de regressão logarítmica
Finalmente, podemos criar um gráfico rápido para visualizar quão bem o modelo de regressão logarítmica se ajusta aos dados:
#plot x vs. y plot(x, y) #define x-values to use for regression line x=seq(from= 1 , to= 15 , length. out = 1000 ) #use the model to predict the y-values based on the x-values y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )), interval=" confidence ") #add the fitted regression line to the plot (lwd specifies the width of the line) matlines(x,y, lwd= 2 )
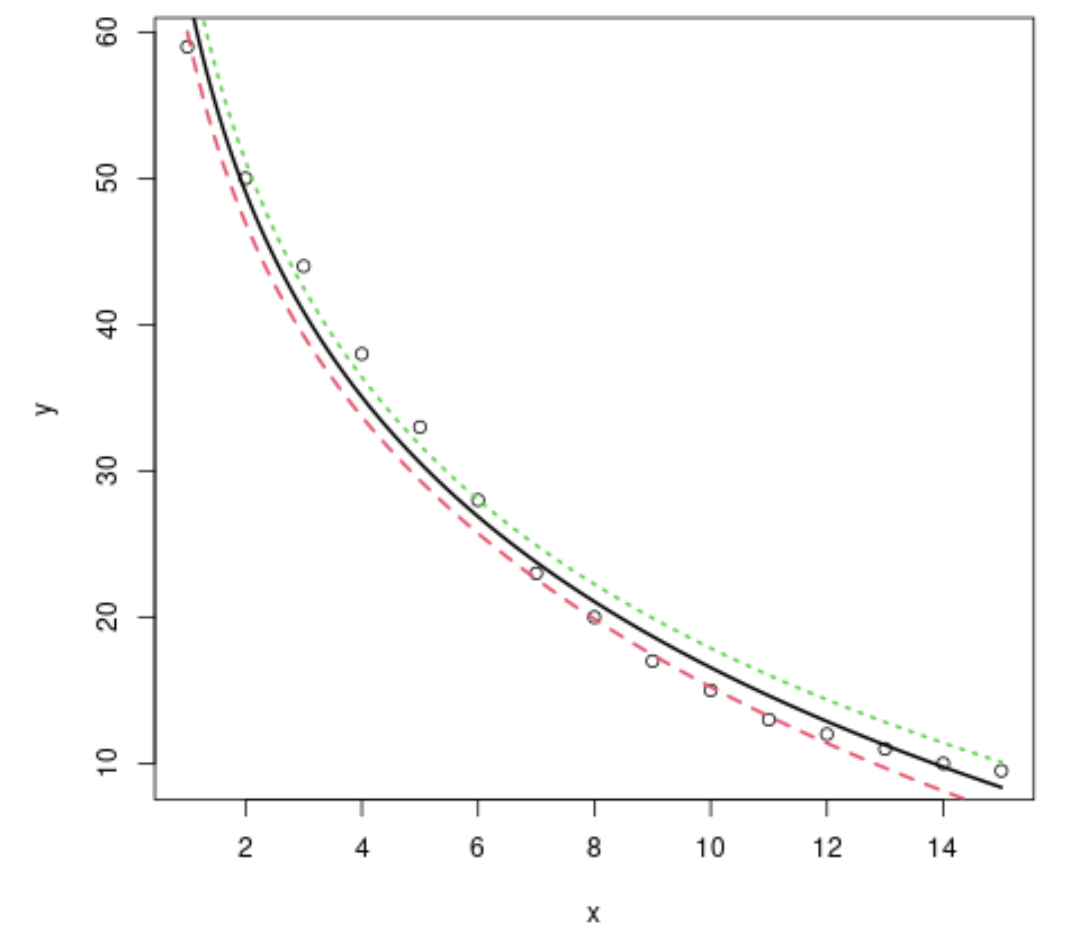
Podemos ver que o modelo de regressão logarítmica faz um bom trabalho ao ajustar este conjunto de dados específico.
Recursos adicionais
Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como realizar regressão quadrática em R
Como realizar regressão exponencial em R
Como realizar regressão polinomial em R