Como realizar um teste de falta de ajuste em r (passo a passo)
Um teste de falta de ajuste é usado para determinar se um modelo de regressão completo fornece ou não um ajuste significativamente melhor a um conjunto de dados do que uma versão reduzida do modelo.
Por exemplo, digamos que queremos usar o número de horas estudadas para prever as notas dos exames dos alunos de uma determinada faculdade. Podemos decidir adaptar os dois modelos de regressão a seguir:
Modelo completo: pontuação = β 0 + B 1 (horas) + B 2 (horas) 2
Modelo reduzido: pontuação = β 0 + B 1 (horas)
O exemplo passo a passo a seguir mostra como realizar um teste de falta de ajuste em R para determinar se o modelo completo fornece um ajuste significativamente melhor do que o modelo reduzido.
Etapa 1: criar e visualizar um conjunto de dados
Primeiro, usaremos o código a seguir para criar um conjunto de dados contendo o número de horas estudadas e as notas obtidas nos exames de 50 alunos:
#make this example reproducible set. seeds (1) #create dataset df <- data. frame (hours = runif (50, 5, 15), score=50) df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2) #view first six rows of data head(df) hours score 1 7.655087 64.30191 2 8.721239 70.65430 3 10.728534 73.66114 4 14.082078 86.14630 5 7.016819 59.81595 6 13.983897 83.60510
A seguir, criaremos um gráfico de dispersão para visualizar a relação entre horas e pontuação:
#load ggplot2 visualization package library (ggplot2) #create scatterplot ggplot(df, aes (x=hours, y=score)) + geom_point()
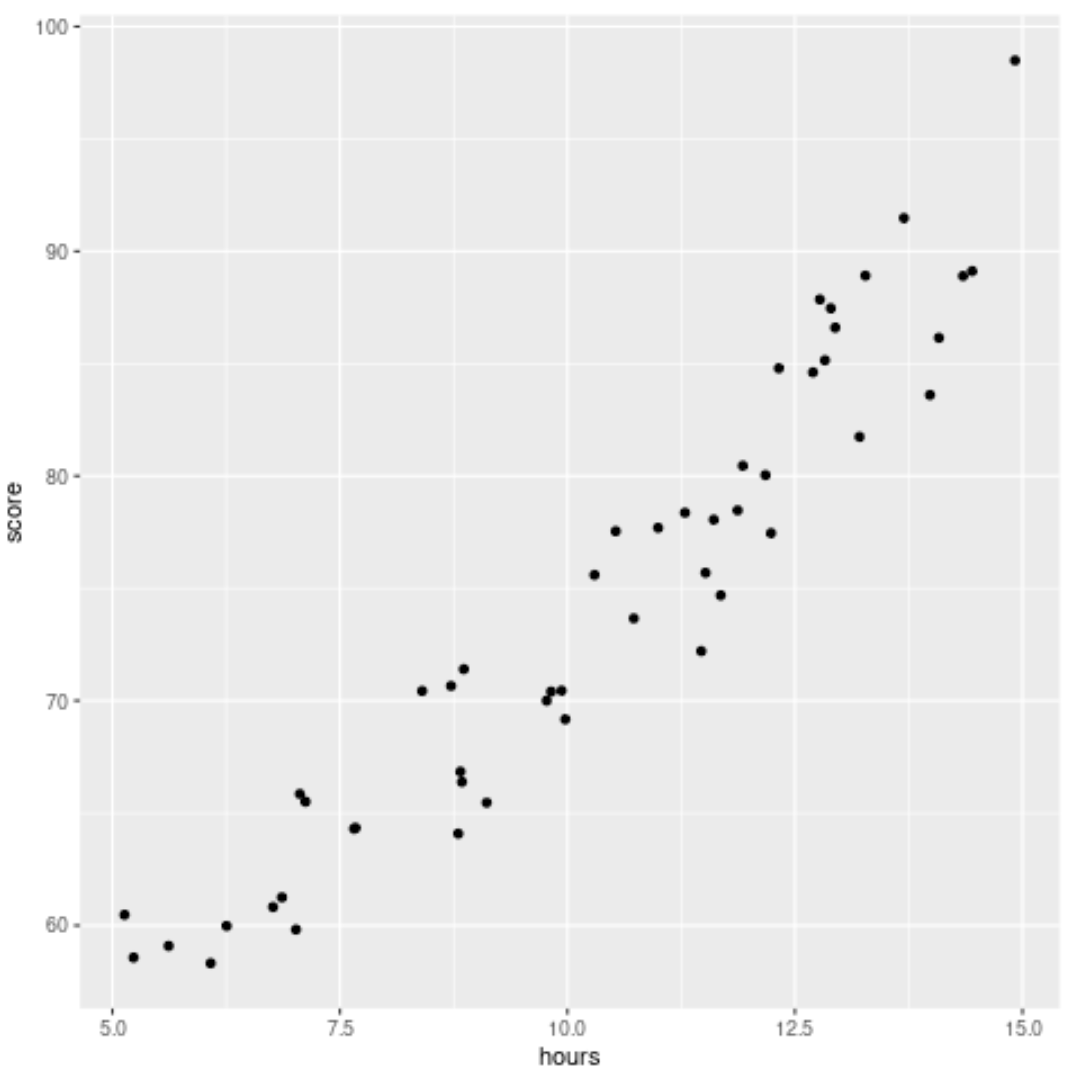
Etapa 2: ajustar dois modelos diferentes ao conjunto de dados
A seguir, ajustaremos dois modelos de regressão diferentes ao conjunto de dados:
#fit full model full <- lm(score ~ poly (hours,2), data=df) #fit reduced model reduced <- lm(score ~ hours, data=df)
Etapa 3: realizar um teste de falta de ajuste
A seguir, usaremos o comando anova() para realizar um teste de falta de ajuste entre os dois modelos:
#lack of fit test
anova(full, reduced)
Analysis of Variance Table
Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 368.48
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
A estatística do teste F é 10,554 e o valor p correspondente é 0,002144 . Como este valor p é inferior a 0,05, podemos rejeitar a hipótese nula do teste e concluir que o modelo completo fornece um ajuste estatisticamente significativamente melhor do que o modelo reduzido.
Passo 4: Visualize o modelo final
Finalmente, podemos visualizar o modelo final (o modelo completo) em relação ao conjunto de dados original:
ggplot(df, aes (x=hours, y=score)) +
geom_point() +
stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) +
xlab(' Hours Studied ') +
ylab(' Score ')
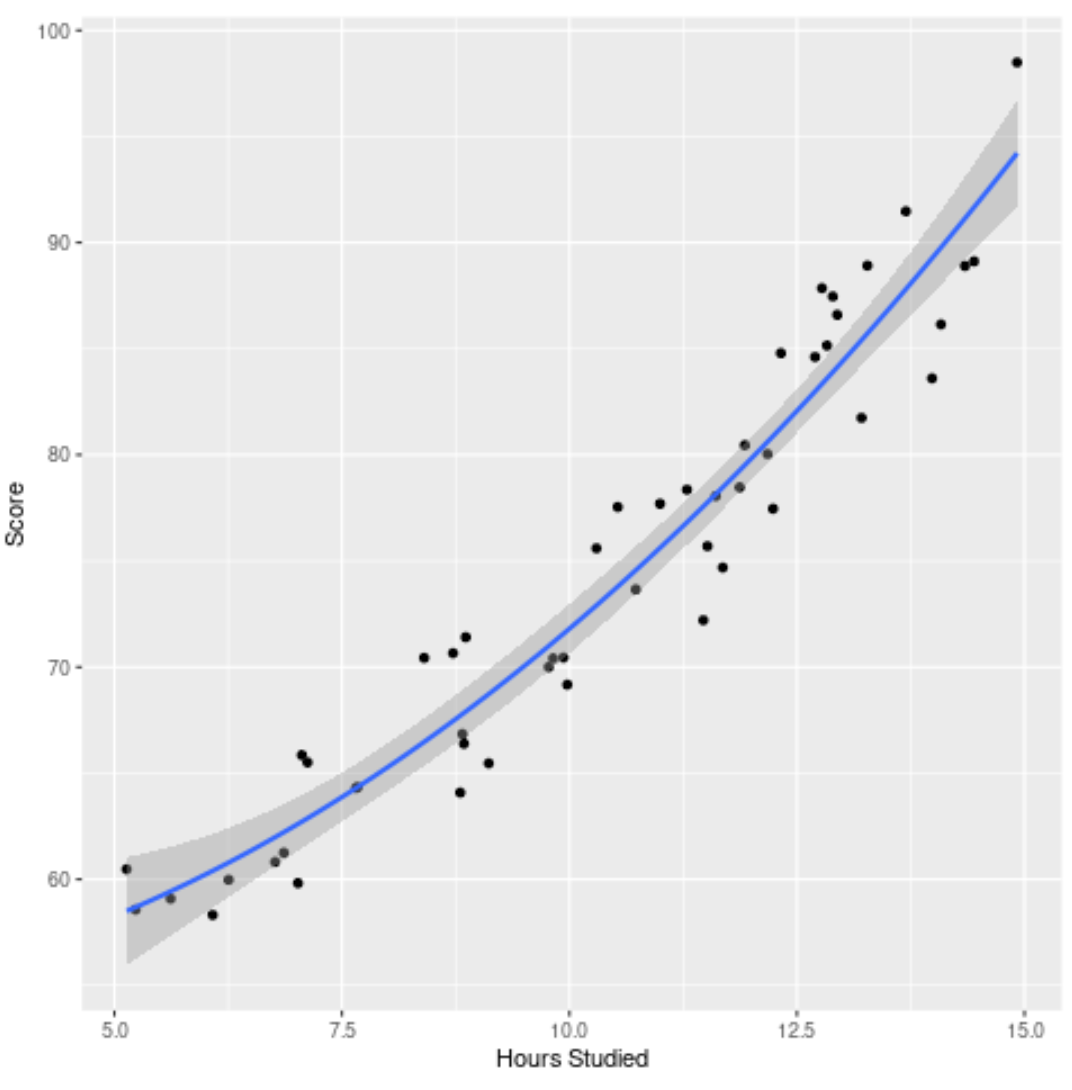
Podemos ver que a curva do modelo se ajusta muito bem aos dados.
Recursos adicionais
Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como realizar regressão polinomial em R